Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 65
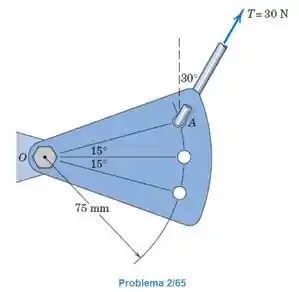
A haste exerce uma força de sobre a guia, como mostrado. Determine o sistema força-binário equivalente em .
Passo 1
E aí meus queridos, tudo bem com vocês? Preparados pra mais uma questãozinha?
Prestem bastante atenção que essa questão é bastante rapidinha, porém, precisa de um pouco da nossa atenção para que a gente não de perca. Pois bem, como queremos o binário equivalente em devemos nos lembrar que ao deslocarmos uma determinada força o seu módulo não vai mudar, ou seja, nós teremos uma força, no ponto desejado, dada por
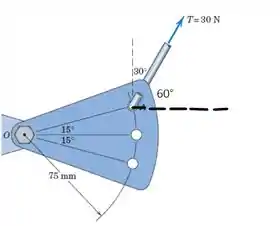
No entanto, em relação ao eixo horizontal nossa força vai estar inclinada de como mostrado na figura acima.
Passo 2
O segundo, e último, elemento que nós precisamos encontrar para o nosso sistema é um binário que iguale o momento gerado pela força na sua posição inicial. Primeiramente, vamos fazer o desenho de como ficaria nossa força em para entendermos como calcular esse binário
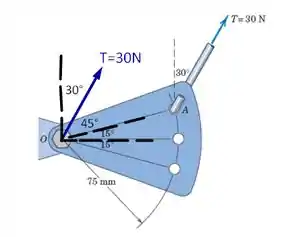
Sendo assim, nosso binário será dado por
Pronto, está resolvido nosso problema sem muita enrolação.