Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 30

Faça referência ao enunciado e à figura do Prob. 2/29. Quando o Pino P está na posição θ = 20°, determine as componentes n e t da força F que a mola de modulo k = 1,4 kN/m exerce sobre o pino. A distância é de r = 400 mm.

Passo 1

Para separar a força entre os eixos será necessário descobrir o ângulo que a força F faz com o eixo n ou y. Vamos cumprir esse desafio separando a figura em dois triângulos retângulos e marcando o eixo y que é paralelo a A B - . Logo o ângulo entre o eixo n e o y formado é igual ao θ como mostra a figura abaixo.

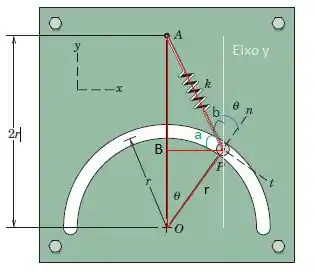
Passo 2

Descobrir o valor do ângulo entre o eixo n e a força:

O valor desse ângulo que chamaremos de α sera:

α =   θ + b  

Agora vamos calcular o valor de b obtendo o valor de a e subtraindo de 90

Então vamos calcular o tamanho de cada segmento:

  A O - =   2 r

B O - = r c o s ( θ )

  B P - = r s e n ( θ )

A B - = A O - -   B O - =   2 r -   r c o s θ = r [ 2 - c o s θ ]

A P - 2 =   B P - 2 + A B - 2   →     A P - =   [ r s e n θ ] 2 + r 2 - c o s θ 2  

Como A P - cos ⁡ a =   B P -  

a = cos - 1 ⁡ B P - A P - = cos - 1 ⁡ r s e n θ [ r s e n θ ] 2 + r 2 - c o s θ 2

Substituindo os valores de θ = 2 0 ° e r = 400   m m   obtemos a = 7 2 , 1 ° .

!!!Fica ligado se sua calculadora está em radianos ou graus. Para converter de graus para radianos basta multiplicar o valor em graus por π e dividir por 180.

Logo b = 90 - a = 17,9 °

Agora podemos obter α .

  α = 17,9 ° + 20 ° = 37,9 °

Passo 3

Calcular F x e F y . Começamos esse paço calculando o valor de δ .

Como δ é o deslocamento da mola que estava inicialmente a distância r. δ =   A P - -   r .

Logo δ =   [ r s e n θ ] 2 + r 2 - c o s θ 2 - r = 45,6   m m , para de θ = 2 0 ° e r = 400   m m  

Agora temos tudo para calcular o valor da força nos eixos x e y.

F n = F cos ⁡ α = k δ cos ⁡ α

F t =   F c o s ( 90 + α ) = k δ cos ⁡ 90 + α  

Substituindo os valores de k = 1 4 00   N / m   , δ = 0 , 046   m e α = 37,9 ° obtemos:

F n = 50,8   N

F t = - 3 9 , 6   N

Resposta

F n = 50,8   N

F t = - 39,6   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O corpo é composto de uma barra curva que tem uma massa ρ por unidade de comprimento. Determine o momento do peso do corpo em relação ao ponto O .
A barra dobrada tem uma massa ρ por unidade de comprimento. Determine o momento do peso de barra em relação ao ponto O .
Ao se abrir uma porta que está equipada com um mecanismo de retorno, uma pessoa exerce uma força P de módulo 32N , como mostrado. A força P e a normal n à face da porta estão em um plano vertical. Cal
O tubo em ângulo reto O A Bd oP r o b .2 / 111 é novamente mostrado aqui. Substitua a força trativa de 750N que o cabo exerce no ponto B por um sistema força-binário no ponto O .
Dois retrofoguetes de 4N do satélite estacionário são acionados simultaneamente, como mostrado. Calcule o momento associado com este binário e diga em relação a que eixos começarão a ocorrer rotações