Teoria
Fala ai e bem vindo ao RespondeAÍ! Na nossa matéria de Mecânica e Resistência dos Materiais você encontra tudo que você precisa para bandar bem na sua prova. Nessa página vamos falar sobre deformações e sobre a Lei de Hooke.
As deformações são um processo natural que acontece quando aplicamos forças em um objeto. Por exemplo um viga de concreto com um peso sobre ela, tem uma tendência natural em sofre algum tipo de deformação. Que provavelmente não será
Existem vários tipos de deformações, e nós já conhecemos algumas delas, como deformações elásticas ou inelásticas mas vamos ver um exemplo que aparece frequentemente na matéria de ResMat:
Vamos dizer que temos uma barra com um comprimento inicial L e que essa barra vai sofrer a ação de uma tração, e essa tração vai aumentar o comprimento da barra em um pequeno fator que vamos chamar de
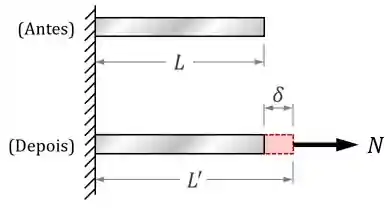
Nossa barra tem inicialmente
As barras reagem às tensões normais
Ou seja, a relação entre a deformação específica do material (
Além da Lei de Hooke, para resolver problemas de Tensão e Deformação é importante que a gente conheça as fórmulas da deformação especifíca:
E da tensão normal média:
Com a combinação dessas três fórmulas, nós conseguimos alcançar na fórmula da variação de comprimenta causada pelo carregamento em uma peça:
Ou seja, é essa fórmula que vai nos dar o valor da variação de comprimento da barra, quando aplicada uma tensão sobre ela. Vamos voltar ao exemplo:
Desenhando esquematicamente nossa barra, e a força aplicada sobre ela:
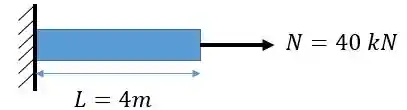
Lembrando que estamos falando de uma barra com área
Logo nossa barra não irá exceder o limite de
Caramba! Engenheiros civis que se cuidem, essas paradas de tensão e deformação estão só no comecinho! Mas vamos com calma que aqui no RespondeAí você consegue todo o conteúdo necessário para mandar bem em Mecânica e Resistência dos Materiais, e ainda tem exercícios resolvidos, vídeos, livros resolvidos, questões de prova e muito mais... Confere um exercício em vídeo aqui rapidão:
Exercício
Confere nossa resolução de um exercício do tópico de Deformação e a Lei de Hooke, para entender direitinho essa matéria:
Uma coluna como a da figura é feita de um concreto com um módulo de elasticidade de
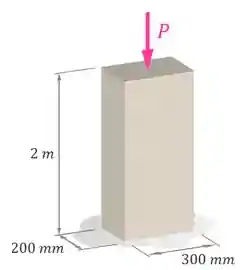
Exercício
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Um cabo de aço de de comprimento é tracionado até atingir um comprimento final de . Determine a variação do comprimento e a deformação sofrida por esse cabo.
Passo 1
O cabo possui um comprimento inicial e um comprimento final .
A variação do seu comprimento vai ser a diferença entre os comprimentos final e inicial:
Já a deformação é uma medida adimensional, dada pela razão entre essa variação e o comprimento original :
Resposta
Exercício Resolvido #2
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 52-2.2.
O comprimento de uma fita elástica delgada não esticada é . Se a fita for esticada ao redor de um cano de diâmetro externo ,cobrindo todo o comprimento circular do tubo, determine a deformação normal média na fita.
Passo 1
A fita possui um comprimento inicial .
Já o seu comprimento final vai ser igual ao perímetro externo do cano de diâmetro .
Lembra aí! O perímetro de um círculo é , onde é o raio do círculo. Reescrevendo esse perímetro em função do diâmetro , encontramos que o comprimento final da fita é igual a .
Aplicando a fórmula da deformação e substituindo , temos:
Substituindo os valores de e , temos:
Calculando tudo, isso dá:
Resposta
Exercício Resolvido #3
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 52-2.3.
A barra rígida é sustentada por um pino em e pelos cabos e . Se a carga aplicada à viga provocar um deslocamento de para baixo na extremidade , determine a deformação normal desenvolvida nos cabos e .
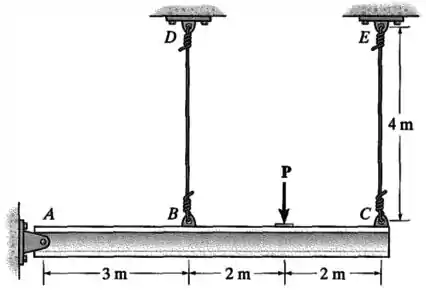
Passo 1
Ambos os cabos tem comprimentos iniciais iguais .
O cabo sofre uma variação de comprimento .
Consequentemente o cabo vai sofrer uma variação de comprimento proporcional a , de acordo com a semelhança de triângulos abaixo:
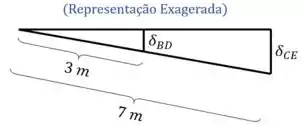
Dessa semelhança de triângulos, tiramos que está para assim como está para , de tal forma que:
Agora que temos em mãos os comprimentos iniciais e as deformações para os cabos e , podemos calcular as deformações nesses cabos:
Substituindo e substituindo os valores de , e , temos:
Agora, temos que tomar um pouco de cuidado uma vez que as deformações devem ser adimensionais.
Isso significa que as unidades em cima e em baixo dessas equações precisam ser iguais.
Podemos ajeitar isso reescrevendo o comprimento de como :
Calculando tudo, isso dá:
Resposta
Exercício Resolvido #4
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 53-2.7.
Os dois cabos estão interligados em . Se a força provocar um deslocamento horizontal de no ponto em , determine a deformação normal desenvolvida em cada cabo.
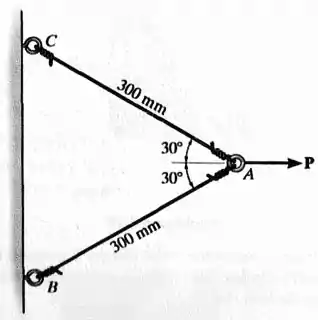
Passo 1
Os dois cabos tem comprimentos iniciais iguais .
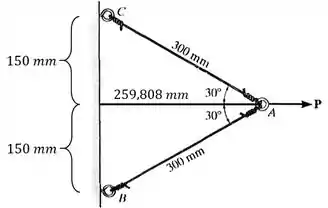
Usando os ângulos fornecidos de , conseguimos deduzir:
- que a distância vertical entre os pontos e e entre os pontos e é igual à ;
- e que a distância entre o ponto e a parede é de ,
Como mostra a imagem abaixo:
Quando o ponto se desloca para a direita, os cabos deixam de ter de comprimento e a distância entre a parede e o ponto sobe de para :
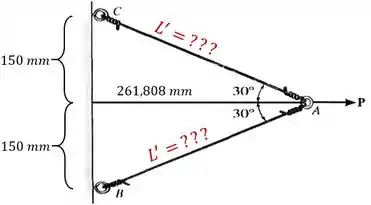
Para encontrar o comprimento final dos cabos, podemos usar o Teorema de Pitágoras:
Calculando, isso dá:
Agora que sabemos os comprimentos inicial e final , iguais para os dois cabos, podemos calcular a deformação nos cabos:
Substituindo os valores de e , temos:
Calculando tudo, isso dá:
Resposta
Exercício Resolvido #5
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 70-3.10.
Uma barra de aço A-36 tem comprimento de e área da seção transversal de . Determine o comprimento da barra se ela for submetida a uma tração axial de . O material tem comportamento elástico linear.
Dados:
Passo 1
A barra possui um comprimento inicial , uma área de seção transversal e é feita de um material com um módulo de elasticidade .
Ela está submetida a uma tração axial de , o que gera nela uma força interna normal .
O exercício quer saber o comprimento final da barra, que vai ser igual ao comprimento inicial mais a variação de comprimento causada pela tração na barra:
Agora vamos nos lembrar...
Combinando as fórmulas da Lei de Hooke (), da tensão normal média () e da deformação (), obtemos uma nova fórmula.
É uma fórmula que relaciona diretamente a variação de comprimento em uma peça com o carregamento a qual ela está submetida:
Então usando essa fórmula, vamos ter que:
Daí que podemos usar essa expressão acima para encontrar diretamente o comprimento final da barra!
Passo 2
Como vimos, temos que:
Substituindo os valores de , , e , temos:
Para entender a situação das unidades na divisão, podemos substituir por :
Dessa forma, vamos ter que as unidades “” e “” se cortam, e assim o resultado da divisão vai sair em !
Calculando a divisão, isso dá:
E assim temos que:
Resposta
Exercício Resolvido #6
Elaboração Própria
Uma coluna da figura é feita de um concreto com um módulo de elasticidade de . Determine a deformação , a variação de comprimento e o comprimento final dessa coluna quando ela estiver sob compressão por uma força de .
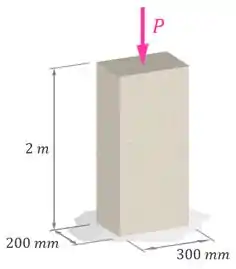
Passo 1
A força de compressão gera na coluna uma força interna normal , que, por sua vez, gera uma tensão normal média .
Para calcular essa tensão , podemos analisar os esforços internos na coluna para encontrar a força normal e usar as dimensões para encontrar a área da seção transversal.
Agora, de acordo com a Lei de Hooke, essa tensão vai corresponder a uma certa deformação na coluna:
Então conhecendo o módulo de elasticidade e a tensão , conseguimos encontrar a deformação na coluna, que é uma das coisas que o exercício quer que a gente determine.
Além disso, sabemos que a deformação é definida como:
E que a variação de comprimento é definida como:
Então sabendo que a coluna tinha um comprimento original , podemos usar as fórmula acima para encontrar a variação de comprimento e o comprimento final da coluna.
Passo 2
Vamos começar avaliando os esforços internos na coluna para encontrar o valor da força normal .
Desenhamos a coluna secionada, adicionamos a força externa e adicionamos a força interna normal apontando para fora da peça:
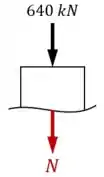
E em seguida, aplicamos o equilíbrio de forças na vertical para relacionar a força normal com a força externa:
Isolando , encontramos que:
Encontramos que a força normal é negativa, ou seja, ela é uma força normal de compressão.
Consequentemente, a tensão normal média e a deformação também vão ser negativas.
Passo 3
Com a força normal encontrada, já temos todas as informações necessárias para aplicar a Lei de Hooke:
Substituir a fórmula da tensão normal média :
E isolar a deformação :
Substituindo os valores , e , temos:
Como , as unidades dessa equação vão todas se cortar.
Calculando tudo, temos:
Essa já é uma das nossas respostas, agora vamos encontrar as outras duas!
Passo 4
Aplicando a fórmula da deformação :
Isolando a variação do comprimento :
Substituindo e , temos:
O que dá:
Como é o mesmo que , isso é o mesmo que:
Por última, a variação do comprimento é a diferença entre o comprimento final e o comprimento inicial :
Isolando o comprimento final , temos:
Substituindo e :
é o mesmo que ou , então:
Ou seja:
Resposta
Exercício Resolvido #7
Prof. João Chafi Hallack et al., Apostila de Resistência dos Materiais 1, Universidade Federal de Juiz de Fora, Março de 2015, pp. 43-4.
Um corpo de prova padronizado, de aço, com de diâmetro, sujeito a uma força de tração de teve um alongamento de para um comprimento de . Admitindo-se que não foi superado o limite de proporcionalidade, estimar o valor do módulo de elasticidade longitudinal do aço.
Passo 1
O corpo de prova tem um comprimento inicial .
Quando submetido a uma tração de , que gera nele uma força interna normal , esse corpo de prova tem uma variação de comprimento .
Além disso, o corpo de prova possui uma seção transversal circular de diâmetro .
Isso significa que a área da seção transversal do corpo de prova pode ser calculada usando a fórmula da área de um círculo em função de seu diâmetro: .
O exercício quer saber o valor do módulo de elasticidade que rege a Lei de Hooke para esse corpo de prova:
A tensão normal média e a deformação normal nessa equação podem ser substituídas pelas suas fórmulas:
Conhecemos , , e , então podemos usar essas fórmulas para encontrar o valor de !
Passo 2
Vamos começar então aplicando a Lei de Hooke:
E substituindo as fórmulas da tensão normal média e da deformação normal :
Em seguida, isolamos o módulo de elasticidade :
Como a área da seção transversal circular pode ser calculada em função de seu diâmetro através da fórmula , temos que:
Substituindo os valores de , , e :
Observando as unidades dessa equação, vemos que o resultado dela vai sair em , que é o mesmo que .
Tendo isso em mente e calculando tudo, obtemos que:
Resposta
Exercício Resolvido #8
Elaboração Própria
O eixo de aço abaixo possui, nos trechos e , uma seção transversal com uma área de , e, no trecho , uma seção transversal com uma área de .
Determine a variação de comprimento total do eixo quando ele está submetido às cargas mostradas na figura, sabendo que ele possui um módulo de elasticidade .
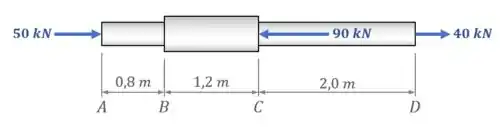
Passo 1
Nesse exercício, queremos encontrar a variação de comprimento do eixo quando ele está submetido ao carregamento mostrado.
Agora, lembra aí!
Já existe uma fórmula para encontrar a variação de comprimento em uma peça com base nas forças que atuam nela:
Nessa fórmula, é a força interna normal, é o comprimento original, é o módulo de elasticidade e é a área da seção transversal da peça. Repare que o enunciado forneceu todos esses valores!
Mas no nosso caso, o eixo tem diferentes trechos (, e ) com diferentes valores de , e .
Então a variação de comprimento total do nosso eixo vai ser a soma das variações de comprimento de cada trecho:
Passo 2
Aplicando a fórmula para cada trecho, e sabendo que o módulo de elasticidade é o mesmo para toda a peça, temos que:
Então para resolver o nosso exercício, precisamos identificar os valores de , e para cada trecho, e, em seguida, aplicar a fórmula acima.
Do enunciado, temos que:
.
E da figura, temos que
Só falta identificar então as forças normais , que precisam ser encontradas através de uma análise de esforços internos nas diferentes seções do eixo.
Mas atenção! A variação do comprimento de cada trecho pode ser positiva OU negativa. O que vai determinar isso é o sinal de .
Isso significa que vamos ter que respeitar as convenções de sinais das forças internas na hora de calcular os valores de , e !
Passo 3
Vamos começar então fazendo uma análise de esforços internos para encontrar os valores das forças internas normais nas diferentes seções do eixo.
1. Começando pelo trecho AB, essa análise fica assim:
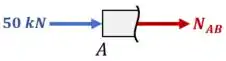
Aplicando o equilíbrio de forças na horizontal, temos:
O que significa que:
2. Já para as seções entre B e C, temos:
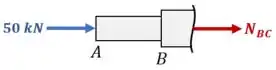
Aplicando o equilíbrio de forças:
De tal forma que:
3. E, finalmente, para o trecho CD:

Aplicando o equilíbrio de forças:
O que significa que:
Passo 4
Encontrados os valores das forças normais , podemos aplicar a fórmula:
Substituindo todos os valores, temos:
Pausa para prestar atenção nas unidades!
Podemos substituir por . Dessa forma, as unidades e vão se cortar e só vai sobrar para o resultado a unidade (metros).
Calculando cada variação individualmente, isso fica assim:
Dá para ter uma noção melhor de cada deformação se reescrevermos elas em :
Somando as deformações individuais de cada trecho, encontramos a deformação total :
Resposta
Exercício Resolvido #9
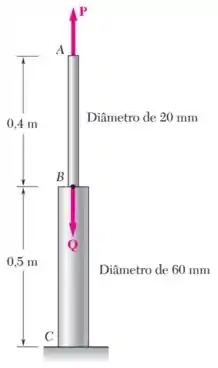
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 87-2.19.
Ambas as partes da barra são feitas de um alumínio para o qual . Sabendo que a intensidade de é , determine o valor de de modo que o deslocamento em seja zero e o deslocamento correspondente de .
Passo 1
Se o trecho da barra sofrer uma variação de comprimento e se o trecho da barra sofrer uma variação de comprimento , então o deslocamento do ponto vai ser a soma dessas variações:
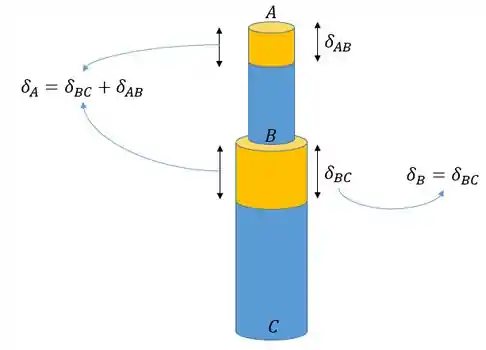
Essas variações de comprimento podem ser calculadas usando a fórmula:
Para tanto, vamos precisar:
- Das forças normais em cada trecho da barra, calculadas em função das forças e através de uma análise dos esforços internos em cada trecho;
- Dos comprimentos originais de cada barra, e , de acordo com a figura do exercício;
- Do módulo de elasticidade do material da barra;
- E das áreas das seções transversais de cada trecho da barra, calculadas a partir de seus diâmetros e , de acordo com a figura.
Ok, e o que é que o exercício quer?
No item , ele quer saber qual deve ser o valor da força tal que o deslocamento em seja zero:
Aí a gente olha na nossa equação do deslocamento de e vê o seguinte:
O que significa que uma variação tem que ser igual ao oposto da outra:
Isso só vai acontecer se uma barra estiver tracionada e a outra comprimida! Dessa forma os deslocamentos podem sim se anular.
Mas nós podemos encontrar essas variações em função das cargas e nas barras!
(Primeiro temos que encontrar as forças internas em função de e e usar a fórmula .)
Então desenvolvendo essa última equação, podemos encontrar qual é o valor da força tal que o deslocamento em seja zero.
Em seguida, no item , o exercício quer que a gente use o valor encontrado de para calcular o deslocamento do ponto , que vai ser igual a de comprimento do trecho :
Passo 2
Primeiro, temos que fazer uma análise dos esforços internos na barra para encontrar o valor da força normal em cada trecho.
Para as seções entre e , o desenho fica assim:

Aplicando o equilíbrio de forças, temos:
O que implica que:
E agora para o trecho , o desenho fica assim:
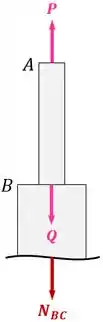
Aplicando o equilíbrio de forças:
Isolando , encontramos:
Passo 3
Como vimos anteriormente, para que o deslocamento em seja zero () é preciso que:
Agora que já temos as forças normais nos trechos e da barra, já estamos prontos para desenvolver essa expressão e descobrir qual é o valor de que garante essa condição.
Aplicando a fórmula para cada trecho, temos:
Não sabemos o valor das áreas das seções transversais da barra.
Mas sabemos que essas áreas são circulares e podem ser calculadas em função de seus diâmetros através da fórmula .
Sendo assim, a equação anterior fica assim:
Cortando os termos em comum dos dois lados, isso fica assim:
Substituindo as expressões encontradas para as forças normais e , temos:
O que é o mesmo que:
Queremos encontrar , então devemos isolá-lo:
Primeiro, isolamos :
E depois isolamos o próprio :
Colocando em evidência, isso fica assim:
Substituindo e substituindo os valores dos diâmetros e dos comprimentos fornecidos pela figura do exercício, temos:
Calculando tudo, isso dá:
Que é a resposta do item !
Passo 4
Para o item , vamos usar o valor encontrado para no item para calcular o deslocamento do ponto , que é igual à variação de comprimento do trecho :
Usando a fórmula para o trecho :
Descrevendo a área em função de seu diâmetro :
Como :
Substituindo os valores de , , , e :
Como , as unidades e vão se cortar e o resultado vai sar em (metros).
Calculando tudo:
Esse número é bem pequeno, então é uma boa reescrever ele em :
Ou seja, o ponto se deslocou para baixo.
Resposta
Exercício Resolvido #10
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 86-2.14.
O cabo de de diâmetro é feito de um aço com . Sabendo que a máxima tensão no cabo não pode exceder e que a deformação do cabo não deve exceder , determine a máxima força que pode ser aplicada conforme mostra a figura.
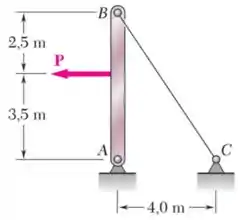
Passo 1
O que está acontecendo?
A viga é mantida em equilíbrio pelas reações horizontal e vertical do apoio em e por uma força “” feita pelo cabo , como mostra o seu DCL (diagrama de corpo livre):
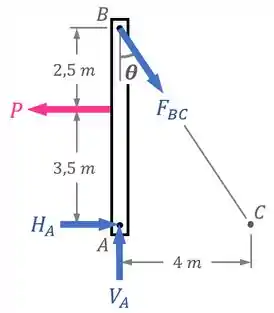
Como reação a essa força , a viga traciona o cabo com uma força de mesma intensidade .
Essa tração no cabo gera nele uma tensão normal média .
Quanto maior for a força , provavelmente maior será a força , de forma a garantir o equilíbrio da viga. Quanto maior for , maior será a tensão no cabo.
O cabo tem um diâmetro , é feito de um aço com módulo de elasticidade e possui um comprimento inicial que pode ser obtido através do teorema de Pitágoras:
E o que é que o exercício quer?
Ele quer saber o valor máximo da força tal que a tensão no cabo não ultrapasse e a variação de comprimento do cabo não ultrapasse :
Mas se a gente for parar pra pensar, essa variação de comprimento máxima corresponde a uma deformação máxima que corresponde a uma tensão máxima.
Então essas condições podem ser reescritas como:
Entre essas duas condições, a que resultar em valores mais restritos para vai ser a condição que vamos usar no restante do exercício, já que assim as duas condições vão estar sendo respeitadas.
Depois que tivermos definido a nossa condição limitante, vamos desenvolver nela a tensão normal média para encontrar o valor máximo da força .
Para tanto, vamos precisar ter antes aplicado as condições de equilíbrio no DCL da viga para encontrar a intensidade da tração no cabo em função da força .
Passo 2
Então primeiro, vamos descobrir qual é a nossa condição limitante:
ou...
Pegando a segunda condição e substituindo os valores:
- ;
- e ,
Temos:
Para comparar essa condição com a outra, vamos querer uma resposta em .
Então reescrevemos como e reescrevemos como :
Calculando tudo, isso dá:
Isso é menor que .
O que isso significa é que bem antes da tensão na corda atingir , a sua variação de comprimento já vai ter atingido (quando a tensão for de ).
Sendo assim, a nossa condição limitante para o restante do exercício vai ser:
Passo 3
Agora, antes de usar a condição para descobrir qual é o valor máximo de , precisamos descobrir como afeta a tensão normal média no cabo.
Como o cabo só está sobre tração por uma força de intensidade , então a força interna normal no cabo vai ser igual a .
Sendo assim, precisamos avaliar o equilíbrio da viga para encontrar em função da força .
Fazendo o Diagrama de Corpo Livre da viga, temos:
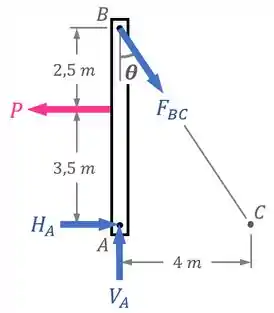
Agora vamos pensar...
Queremos relacionar e .
A condição de equilíbrio que vai nos permitir fazer isso mais facilmente vai ser aquela que não envolve as outras forças ( e ), que é o equilíbrio de momentos em relação ao ponto :
A força vai fazer um momento no sentido anti-horário () com um braço de .
Quanto a força ela vai ter:
- Uma componente vertical que não vai gerar momento (por ter um braço de );
- E uma componente horizontal que vai gerar um momento no sentido horário () com um braço de .
Então o somatório de momentos fica assim:
Isolando , temos:
Substituindo por :
Como a intensidade de é a mesma intensidade da tração no cabo e, consequentemente, a mesma intensidade da força normal no cabo, temos que:
Passo 4
Já sabemos como afeta a força normal e, consequentemente, a tensão no cabo.
Então já podemos aplicar a condição limitante:
Substituindo a fórmula da tensão normal média:
A área da seção transversal do cabo pode ser encontrada a partir de seu diâmetro de através da fórmula .
Substituindo isso e a expressão encontrada para no passo anterior, temos:
Isso é o mesmo que:
Simplificando e juntando tudo, isso fica assim:
Queremos descobrir o valor máximo de , então vamos isolá-lo:
Antes de calcular tudo, precisamos descobrir o valor de .
Observando a figura do exercício:
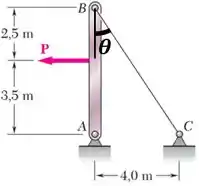
Vemos que o seno de é igual ao cateto de sobre a hipotenusa, que pode ser calculada pelo teorema de Pitágoras:
Substituindo esse seno e o diâmetro na equação anterior, temos:
Megapascal () é o mesmo que um newton por milímetro quadrado (), então o resultado desse cálculo vai sair em newtons ():
Esse número é um pouco grande, então podemos reescrevê-lo em :
O valor máximo de vai ocorrer quando essa expressão for uma igualdade, então:
Resposta
Exercício Resolvido #11
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 83-3.41.
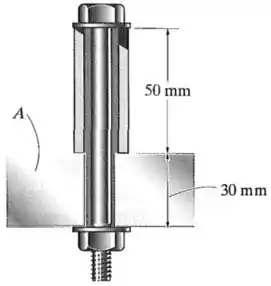
O parafuso de de diâmetro é feito de uma liga de alumínio e está instalado em uma luva de magnésio com diâmetro interno de e diâmetro externo de . Se os comprimentos originais do parafuso e da luva forem e , respectivamente, determine as deformações na luva e no parafuso se a porca do parafuso for apertada de tal modo que a tensão no parafuso seja de . Considere que o material em é rígido.
, .
Passo 1
O que está acontecendo?
Quando as porcas são apertadas, elas comprimem a luva e o material rígido.
Como reação, a luva e o material rígido empurram as porcas de volta, o que gera uma tração no parafuso.
Como essa tração e essa compressão são um par ação-reação, elas tem a mesma intensidade.
Agora...
O enunciado do exercício fala que a “tensão” no parafuso é de ...
Sabendo que o parafuso vai ser tracionado nesse sistema parafuso/porca, podemos concluir que deve ser na verdade a força de tração no parafuso.
E se o nosso parafuso está sendo tracionado por uma força de , isso significa que a nossa luva está sendo comprimida por uma força de .
E o que é que o exercício quer?
Ele quer saber o valor das deformações do parafuso e da luva.
Da Lei de Hooke, temos que:
Isolando , isso fica assim:
E como é a tensão normal média nas peças, então:
Agora vamos ver...
A tração de gera no parafuso uma força interna normal e a compressão de na luva gera nela uma força interna normal .
As áreas das seções transversais e podem ser calculadas a partir do diâmetro do parafuso e dos diâmetros internos e externo da luva e .
E ainda conhecemos os módulos de elasticidade do parafuso e da luva .
Então podemos usar essa última fórmula para calcular as deformações !
Passo 2
Aplicando a fórmula , que encontramos a partir da Lei de Hooke e da fórmula da tensão normal média, para o parafuso, temos:
A área da seção transversal do parafuso, que é circular, pode ser calculada a partir de seu diâmetro através da fórmula , então:
Substituindo os valores , e :
, então todas as unidades dessa equação vão se cortar.
Calculando tudo, encontramos:
Se quisermos, podemos dar uma unidade para qualquer resultado de deformação , como ou , mas isso não é necessário.
Passo 3
E agora aplicando a mesma fórmula para a luva:
A seção transversal da luva é como um anel, com um diâmetro externo e um diâmetro interno .
A sua área pode ser calculada como a diferença das áreas dos círculos formados por esses diâmetros. Como a área do círculo em função do diâmetro é , temos:
Substituindo os valores , , e :
Como , todas as unidades dessa equação vão se cortar.
Calculando tudo, isso dá:
Resposta
Exercício Resolvido #12
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 92-4.12.
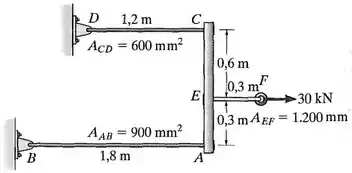
O conjunto é composto por três hastes de titânio (Ti-6A1-4V) e uma barra rígida . A área da seção transversal de cada haste é dada na figura. Se uma força de for aplicada ao anel , determine o ângulo de inclinação da barra .
Dados:
Passo 1
A primeira coisa que vamos fazer nesse exercício é desenhar um diagrama de corpo livre da barra rígida (como o da imagem abaixo) e aplicar as condições de equilíbrio nela.
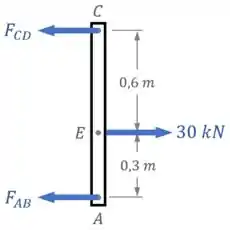
Com isso, vamos poder descobrir os valores das forças e que as hastes e fazem na barra rígida em função da força de que a haste faz.
Como reação a essas forças e , a barra faz trações de mesma intensidade nas hastes:
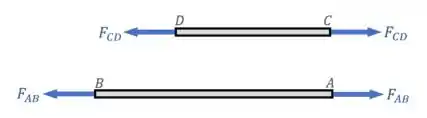
E assim, as forças internas normais nas hastes vão ser iguais à essas trações e :
Conhecendo as forças normais nas hastes, e identificando no enunciado e na figura:
- Os comprimentos iniciais e das hastes;
- O módulo de elasticidade do material das hastes;
- E as áreas e das seções transversais das hastes,
vamos poder usar a fórmula abaixo para encontrar as variações de comprimento e nas hastes:
Obs: Essa fórmula é aquela vem da união da Lei de Hooke com as fórmulas da tensão normal média e da deformação normal !
Sabendo as variações de comprimento e , vamos poder desenhar a nova configuração da barra e usar esse desenho para encontrar o ângulo de inclinação da barra, que é o que o exercício quer!
Passo 2
Começando pelo Diagrama de Corpo Livre da barra :
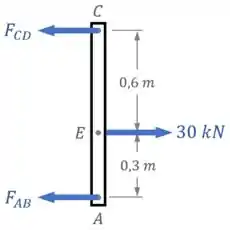
Duas condições de equilíbrio podem nos ajudar a relacionar essas forças aqui: o equilíbrio de momentos em relação a um ponto (vamos escolher o ponto ) e o equilíbrio de forças na horizontal:
Quanto ao somatório de momentos em relação ao ponto :
A força vai gerar um momento no sentido anti-horário () com um braço de .
Já a força de vai gerar um momento no sentido horário () com um braço de .
Sendo assim, o somatório de momentos fica assim:
Isolando , temos:
O que dá:
E quanto ao somatório de forças na horizontal, temos:
Isolando :
Encontramos que , então:
Por último, observando as hastes:
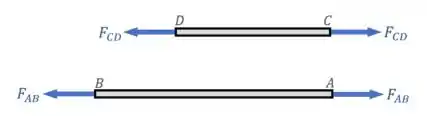
Vemos que elas estão sob tração pura, o que significa que a força interna normal em cada haste vai ser igual à força de tração em cada haste:
Passo 3
Agora que sabemos o valor das forças normais nas hastes, podemos aplicar a fórmula para encontras as variações de comprimento em cada haste.
Para a haste , temos:
Substituindo todos os valores:
, então as unidades e vão se cortar e o resultado disso tudo vai sair em metros ():
Fazendo tudo de novo para a haste , temos:
Passo 4
Determinadas as variações de comprimento de cada haste, podemos desenhar a nova configuração da barra .
Como os pontos e das hastes estão fixos, então toda a variação de comprimento das hastes implicou no deslocamento dos pontos e .
Na imagem abaixo, os pontos originais são e , os pontos deslocados são e , e as variações e são o deslocamento que houve entre esses pontos:
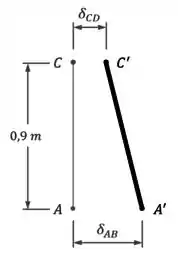
Agora, queremos saber o ângulo de inclinação da barra rígida em sua nova posição .
Então vamos definir o ângulo entre a inclinação antiga (vertical) e a inclinação nova como .
Esse ângulo vai fazer parte de um triângulo retângulo em que:
1. O cateto adjacente vai ser a distância vertical entre e , que vamos dizer que é igual à distância vertical de entre e ;
(Essa aproximação é aceita e necessária em exercícios desse tipo!)
& 2. O cateto oposto vai ser a diferença entre os deslocamentos de e , e .
Como mostra a imagem abaixo:
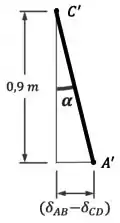
Desse desenho, conseguimos tirar que:
Substituindo e :
Isolando , temos:
O que dá: