Um vaso de pressão de 300mm de diâmetro externo é fabricado com chapa de aço de 6,35mm de espessura, que é soldada ao longo de uma hélice formando um ângulo de com a horizontal. Sabendo-se que a pressão no interior do vaso é de e que uma força axial P de é aplicado no centro da placa superior, determinar:
- A tensão normal perpendicular a solda;
- A tensão de cisalhamento paralela à solda.
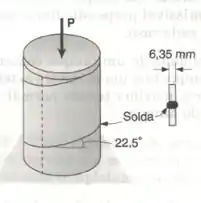
Passo 1
Então galera, essa questão pode parecer que foge da nossa realidade, mas muito pelo contrário, ela só vai acoplar um conceito novo ao nosso problema, e esse conceito é muito simples. Você lembra como era o nosso elemento infinitesimal quando o mesmo estava sujeito a um conjunto de tensões?
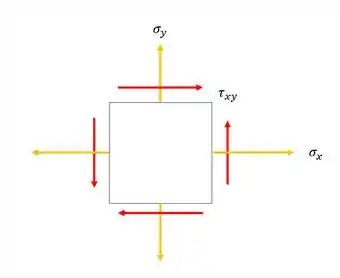
Porém, sempre que tratamos vasos de pressão, ou esferas de pressão, calculávamos um estado de tensões sem tensão de cisalhamento, ou seja, só tensões principais, que é exatamente isso aqui que calculamos:
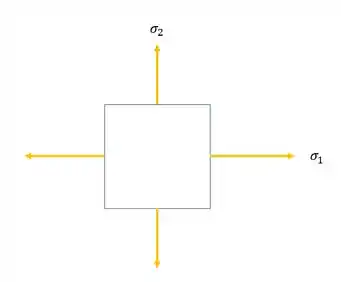
Agora pensa no seguinte, estamos colocando uma tensão normal vertical que comprime o nosso tanque na direção vertical, ou seja, sabemos que a tensão que ela causa é dada por:
Em que a A é dada por:
E essa tensão normal por ser uma compressão, vai diminuir a nossa tensão 2, sendo assim, teremos que:
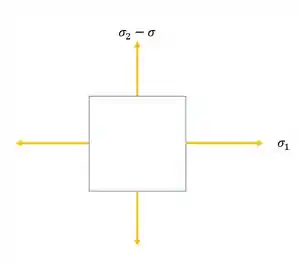
Onde as tensões normais são calculadas da seguinte maneira.
- Sabemos que a nossa tubulação é cilíndrica e não esférica, nesse caso, usaríamos as seguintes equações:
- Sabemos que o nosso diâmetro dado, é o diâmetro externo, ou seja, precisamos descontar a espessura, sendo assim temos que:
- E sabemos que é a espessura
- é a pressão que age na nossa estrutura
Até aqui tudo certo, certo? Mas ai entra uma coisa bem legal, lembra que agora queremos as tensões que agem na nossa solda, que está girada de um ângulo com relação ao estado plano de tensões principais.
Agora pensa comigo, sempre que eu tenho um estado plano de tensões, e giro esse estado plano de tensões, qual a nova fórmula que eu uso para isso???? EXATAMENTE as nossas três formulazinhas que usamos quando queremos girar a nossa seção, com isso teremos que:
Agora sim temos toda a matéria prima para resolver o nosso problema, vamos nessa??
Passo 2
Sabemos pelo enunciado que:
Calculando o raio, temos que:
Calculando a tensão, teremos que:
E agora só falta a tensão normal devido a carga aplicada, e para isso temos as seguintes equações:
Em que a A é dada por:
E assim o nosso elemento infinitesimal é dado por:
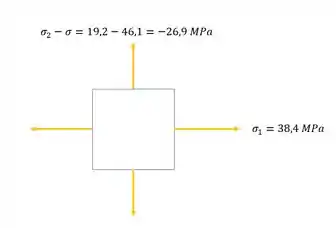
E assim resolvemos metade do nosso problema, agora vamos girar a nossa seção para encontrarmos as tensões na nossa solda. Fica tranquilo que já estamos no finalzinho, vamos dar um último gás.
Passo 3
Sabemos que:
Substituindo teremos que:
Começaremos com a tensão em x.
Vamos para a próxima tensão.
Agora vamos para a tensão em y.
Olhando o nosso elemento girado, temos que:
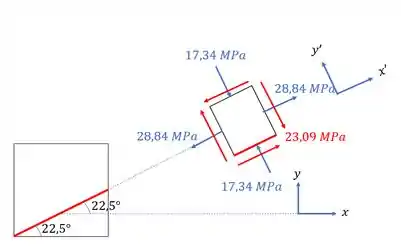
Assim temos que:
- Tensão normal perpendicular ao filete é dada pela .
- Tensão cisalhante na solda.