Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Propriedades Mecânicas e o Diagrama Tensão-Deformação

Ver Todos os Exercícios

Teoria

Opaaa, seja bem vindo ao Responde Aí! Bora conhecer o Gráfico Tensão de Deformação?!

Ensaio de Tração

Antes de qualquer coisa a gente precisa falar do Ensaio de Tração! Na Resistência dos Materiais, o nosso objetivo é descobrir em que condições as coisas falham. Para isso, precisamos calcular as tensões e deformações nas peças, além de conhecer como os materiais se comportam quando submetidos a essas tensões e deformações!

Um passo super importante nessa descoberta é o ensaio de tração.

Ensaio de Tração
Ensaio de Tração

Nele, um pequeno corpo de prova, feito do material que estiver sendo estudado, é colocado em uma máquina que vai gradualmente tracionando esse corpo, até ele quebrar, como podemos observar acima.

Mas o mais interessante é que a máquina em que é feito o ensaio de tração registra continuamente a força aplicada e a variação de comprimento correspondente no corpo de prova. E é com esses dados que a gente pode montar o gráfico Tensão x Deformação!

Diagrama Tensão-Deformação

O Diagrama Tensão-Deformação é um gráfico que relaciona a tensão na qual o material é submetido e a deformação sofrida . Na figura abaixo podemos ver a carinha dele:

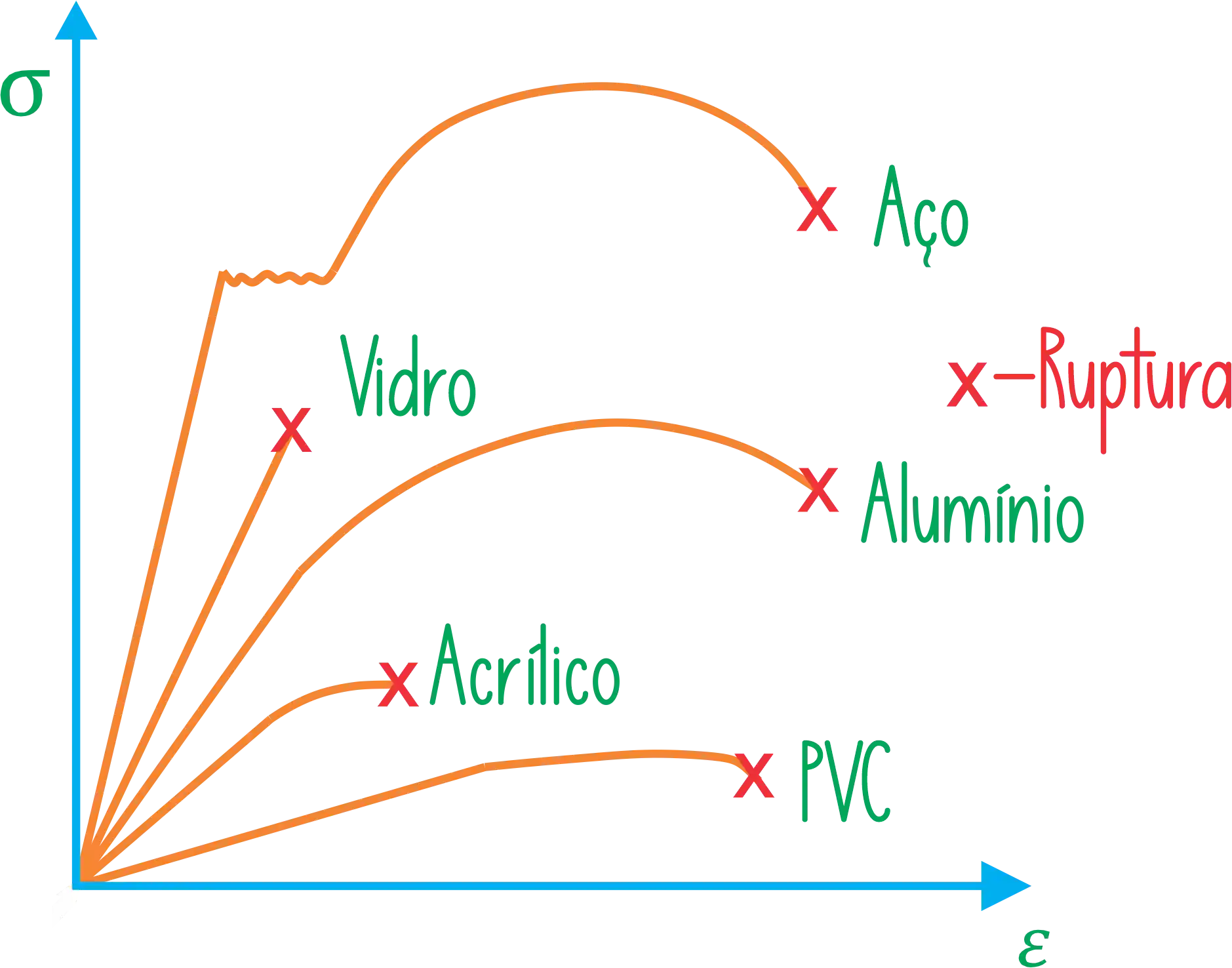
Gráfico Tensão de Deformação
Gráfico Tensão de Deformação

No gráfico acima a gente pode observar como se comporta vários materiais quando submetidos à tração… por enquanto essas curvas podem não fazer nenhum sentido pra você! Mas hoje a gente vai entender cada aspecto desse gráfico!

Ahh…a tensão do eixo é obtida dividindo força aplicada, ao corpo de prova, pela área da sua secção transversal!

Região Elástica e o Módulo de Elasticidade

A primeira coisa que conseguimos observar, é que todos os materiais mostrados no gráfico a cima tem uma região linear!

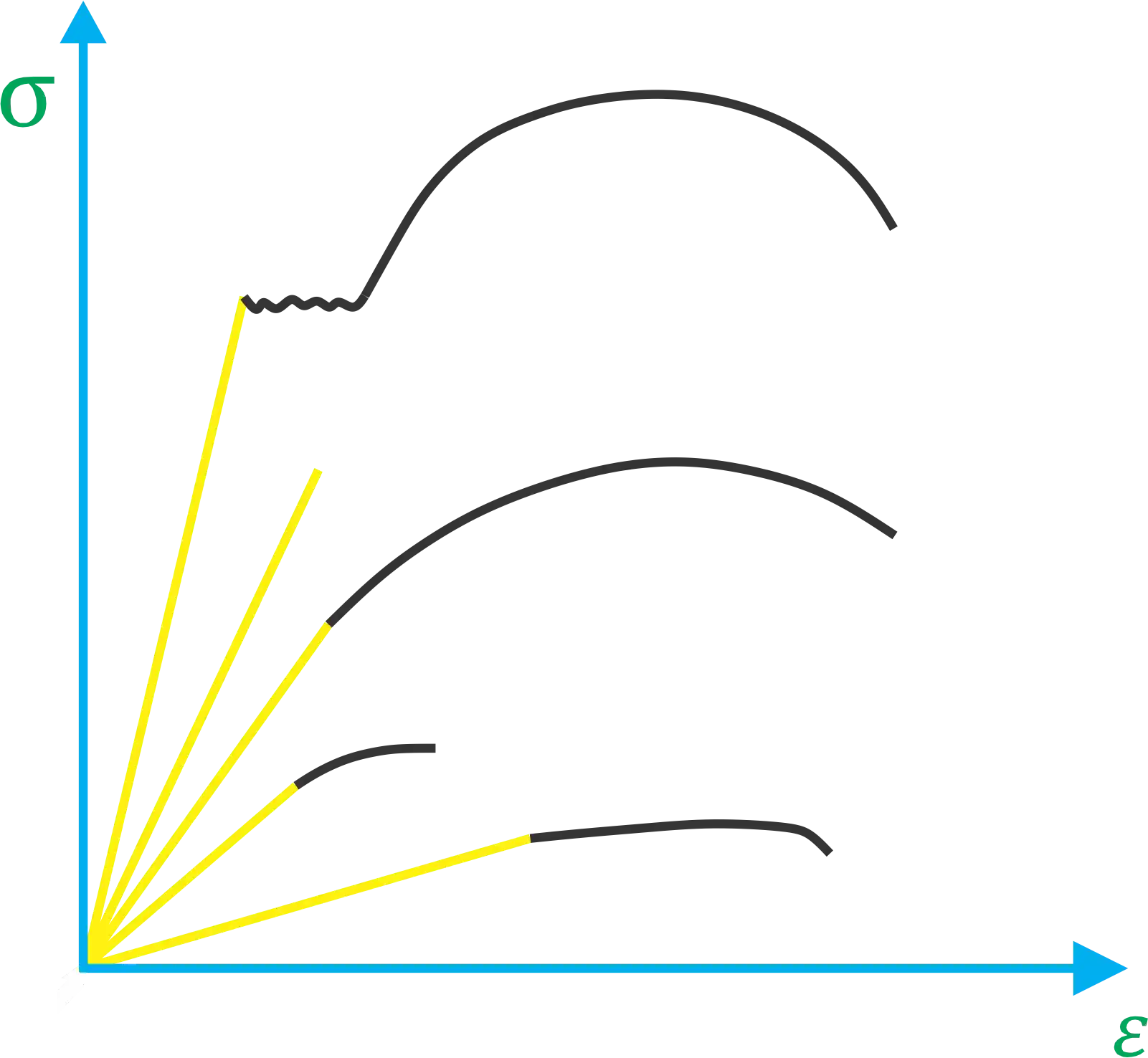
Região Elástica
Região Elástica

Essa região onde a deformação varia linearmente com a tensão aplicada é chamada de região elástica ou região linear-elástica. Nessa região, os materiais se comportam de acordo com a Lei de Hooke e as deformações são reversíveis, ou seja, a deformação some quando o material deixa de ser carregado!

O que faz total sentido, afinal quando a gente estica um elástico e solta, ele volta ao seu tamanho original! 😱 😉

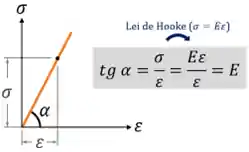
Nessa região, o módulo de elasticidade de um material vai ser igual à tangente do ângulo de inclinação da região elástica desse material:

Região Elástica
Região Elástica

Região Plástica

Após a região elástica, existe uma segunda região, chamada de região plástica! Se liga só:

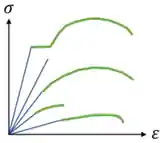
Região Plástica
Região Plástica

É bom a gente ter em mente que alguns materiais que só possuem região elástica ou só possuem região plástica. O vidro é um exemplo de material que só possui região elástica!

Na região elástica, as deformações:

  • Deixam de ser elásticas, ou seja, reversíveis e descritas pela Lei de Hooke;
  • E passam a ser plásticas, isso é irreversíveis, e são descritas somente pelo Diagrama Tensão-Deformação.

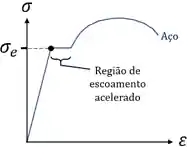
Resistência ao Escoamento

Quando os materiais se deformam irreversivelmente, a gente fala que eles escoaram. Como, em muitas situações, a gente quer evitar esse escoamento, precisamos definir a tensão máxima que pode ser atingida pelo material antes dele escoar. Essa tensão máxima é chamada de Resistência ao Escoamento, ou Tensão de Escoamento e é representada por :

Resistência ao Escoamento
Resistência ao Escoamento

Você também pode conferir esse conteúdo em vídeo:

Limite de Resistência a Tração

Às vezes, permitimos que os materiais se deformem plasticamente, mas ainda precisamos garantir que a tensão no material não vai superar a tensão máxima que ele consegue aguentar.
Essa tensão máxima é chamada de Limite de Resistência a Tração, é representada por á ou , e é dada pelo ponto mais alto de cada diagrama:

Limite de Resistência a Tração de diferentes materiais
Limite de Resistência a Tração de diferentes materiais

Estricção ou Necking

Alguns materiais tem uma queda de tensão no final de seus diagramas, indicada pela cor vermelha na figura abaixo:

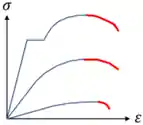
Gráfico Tensão de Deformação: Empescoçamento
Gráfico Tensão de Deformação: Empescoçamento

O que acontece é que esses materiais, ao passarem das suas tensões máximas σ_máx, sacrificam uma parte deles para se deformarem mais ainda:

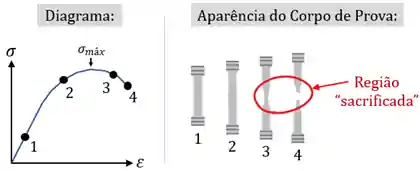
Empescoçamento
Empescoçamento

O nome correto desse efeito é estricção. Mas você pode entender ele como um “empescoçamento” (do inglês, necking). Quando esse efeito acontece, o pescoço da peça se deforma tanto que ele acaba aliviando a deformação no resto da peça, causando a queda de tensão. Apesar disso, a tensão no pescoço em si só aumenta a medida que ele fica mais fino, e, eventualmente, a peça se rompe.

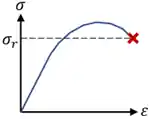
Tensão de Ruptura

Por fim, além de e á, existe um valor de tensão não muito usado, mas que ainda existe, que é a tensão de ruptura . Ela é a tensão no último ponto do diagrama tensão-deformação do material, que é o ponto em que o material se rompe de vez:

Tensão de Ruptura
Tensão de Ruptura

Materiais Dúcteis e Frágeis

Observando os exemplos que usamos, podemos classificar os materiais em dúcteis e frágeis!

Materiais Dúcteis

Os materiais dúcteis são capazes que sofrer grandes deformações antes de se romperem:

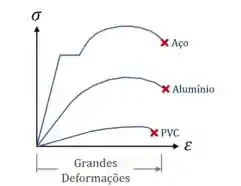
Diagrama de Materiais Dúcteis
Diagrama de Materiais Dúcteis

Esse nome vem da ductilidade, que é a propriedade que alguns desses materiais tem de poderem ser estirados no formato de um fio. Os materiais que sofrem estricção (“empescoçamento”) são sempre dúcteis.

Materiais Frágeis

Os materiais frágeis sofrem ruptura após pequenas deformações:

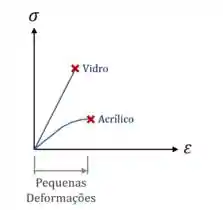
Gráfico Tensão de Deformação: Materiais frágeis
Gráfico Tensão de Deformação: Materiais frágeis

Nos materiais frágeis o Limite de Resistência a Tração á é igual à tensão de ruptura .
Apesar do nome, os materiais frágeis ainda podem ter uma resistência á alta, como é o caso de alguns materiais cerâmicos. Além disso, muitos materiais frágeis têm uma resistência à compressão bem maior que a sua resistência à tração, como é o caso do concreto.

Agora vamos praticar com exercícios?

Materiais Dúcteis e Frágeis

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

A imagem abaixo apresenta o diagrama tensão-deformação de um material dúctil fictício.

Identifique nessa imagem as seguintes propriedades desse material:

( a ) Módulo de Elasticidade E ;

( b ) Limite de Resistência ao Escoamento σ y ;

( c ) Limite de Resistência a Tração σ m á x ;

( d ) Tensão de Ruptura σ r .

Passo 1

Quanto ao item ( a ) :

O módulo de elasticidade E do nosso material pode ser calculado através da razão entre qualquer par de valores de tensão σ e deformação ε na região linear-elástica do material:

E = σ ε

Se a gente for observar o ângulo α de inclinação da região linear-elástica do material, vamos ver como a sua tangente vai ser igual a σ / ε = E :

Dessa forma, temos que o ângulo de inclinação da região linear-elástica vai ser igual a a r c t g   E .

Quanto ao item ( b ) :

Esse material tem uma região de aumento acelerado da deformação ε sem um aumento significativo da tensão σ :

Dessa forma, o Limite de Resistência ao Escoamento σ y desse material vai ser a tensão no ponto imediatamente anterior à essa região de escoamento inicial e acelerado.

Quanto aos itens ( c ) e ( d ) :

Por fim, temos que:

  • O Limite de Resistência a Tração σ m á x de um material é igual à tensão no ponto mais alto do Diagrama Tensão-Deformação;
  • E a tensão de ruptura σ r é igual à tensão no ponto final do diagrama.

Identificando todas essas propriedades na imagem, chegamos a nossa resposta:

Resposta

Exercício Resolvido #2

Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 83-3.40.

Ao ser submetido a um ensaio de tração, um corpo de prova de liga de cobre com comprimento de referência de 50   m m sofre uma deformação de 0,40   m m / m m quando a tensão é de 490   M P a . Se σ e   =   315   M P a quando ε e =   0,0025   m m / m m , determine a distância entre os pontos de referência quando a carga é aliviada.

Passo 1

O que está acontecendo?

Inicialmente, a distância entre os pontos de referência do corpo de prova possuía um comprimento L = 50   m m .

Em seguida, o corpo foi carregado até atingir uma deformação ε = 0,40   m m / m m e uma tensão σ = 490   M P a .

Como essa tensão σ = 490   M P a atingida no corpo é maior que a resistência ao escoamento σ e = 315   M P a , podemos afirmar com certeza que o corpo escoou (entrou na região plástica).

Com isso, a deformação total ε = 0,40   m m / m m atingida pelo corpo é igual a soma de uma deformação elástica ε e com uma deformação plástica ε p :

ε = ε e + ε p

Agora, quando a carga é aliviada, a deformação elástica ε e (que é reversível) é recuperada, enquanto que a deformação plástica ε p (que é irreversível) é mantida.

Dessa forma, a deformação final no corpo vai ser igual à deformação plástica:

ε p = ε - ε e

Como a recuperação da deformação elástica segue a Lei de Hooke, vamos ter que ε e = σ / E , de tal forma que:

ε p = ε - σ E

Onde:

  • ε e σ são a deformação e a tensão atingidas no corpo;
  • E E é o módulo de elasticidade do material, que pode ser calculando dividindo a resistência ao escoamento σ e = 315   M P a pela deformação correspondente ε e = 0,0025   m m / m m .

E o que é que o exercício quer?

Ele quer saber a distância final entre os pontos de referência do corpo de prova.

Ou seja, ele quer saber o comprimento final L ' dessa distância, que vai ser igual ao comprimento inicial L mais uma variação de comprimento δ :

L ' = L + δ

Agora, como a deformação final no corpo vai ser ε p , vamos ter que δ = L ε p , de tal forma que:

L ' = L + L ε p

⇓

L ' = L ( 1 + ε p )

Passo 2

Primeiro, vamos encontrar o módulo de elasticidade E do material!

Considerando que o material se comporta linear-elásticamente no ponto de escoamento e , o módulo de elasticidade E pode ser calculado a partir da Lei de Hooke nesse ponto:

σ e = E ε e

⇓

E = σ e ε e

Substituindo os valores de σ e e ε e fornecidos pelo enunciado, isso fica assim:

E = 315   M P a 0,0025   m m / m m

O que dá:

E = 126000   M P a

Passo 3

Com o módulo de elasticidade E calculado, agora podemos calcular a deformação final no corpo:

ε p = ε - σ E

Subsituindo os valores atingidos ε = 0,40   m m / m m e σ = 490   M P a e o módulo de elasticidade E = 126000   M P a , isso fica assim:

ε p = ( 0,40 ) - 490   M P a 126000   M P a

Calculando, isso dá:

ε p = 0,396 1 -   m m / m m

Passo 4

Finalmente, podemos calcular o comprimento final L ' entre os dois pontos de referência do corpo de prova:

L ' = L ( 1 + ε e )

Substituindo L = 50   m m e ε = 0,3961 1 -   m m / m m , temos:

L ' = 50   m m ( 1 + 0,396 1 - )

Calculando isso, encontramos nossa resposta:

Resposta

L = 69,806   m m

Exercício Resolvido #3

Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 70-3.11.

O diagrama tensão-deformação para o polietileno que é utilizado para revestir cabos coaxiais é determinado por um ensaio com um corpo de prova com comprimento de referência de 250   m m . Se uma carga P aplicada ao corpo de prova desenvolver uma deformação ε   =   0,024   m m / m m , determine o valor aproximado do comprimento do corpo de prova medido entre os pontos de referência quando a carga é removida. Considere que o corpo de prova se recupere elasticamente.

Passo 1

O que está acontecendo?

O corpo de prova tem um comprimento inicial L = 250   m m e foi carregado até atingir uma deformação ε = 0,024   m m / m m , o que corresponde a uma tensão σ = 26   M P a :

Ok!

Agora vamos pensar...

A deformação total ε no corpo é igual à soma das deformações elástica ε e (reversível) e plástica ε p (irreversível) que foram sofridas pelo corpo:

ε = ε e + ε p

Dessa forma, quando o corpo é descarregado, ele vai recuperar a deformação elástica ε e e a deformação final nele vai ser igual à deformação plástica ε p (que não é recuperada):

ε p = ε - ε e

E, como a recuperação da deformação elástica ε e sempre segue a Lei de Hooke, temos que:

ε e = σ E

Sendo assim, a deformação final no corpo vai ser:

ε p = ε - σ E

Onde ε é a deformação de 0,024   m m / m m e σ é a tensão de 26   M P a que foram atingidas pelo corpo.

E o que é que o exercício quer?

Ele quer saber qual é o comprimento final L ' do corpo de prova depois que carga é removida.

Esse comprimento final L ' vai ser igual ao comprimento inicial L do corpo mais a variação de comprimento δ sofrida:

L ' = L + δ

E a variação de comprimento δ vai ser igual ao comprimento inicial L multiplicado pela deformação final ε p , de tal forma que:

L ' = L + L ε p

⇓

L ' = L ( 1 + ε p )

Então como vamos resolver o exercício?

Primeiro, vamos ter que encontrar o módulo de elasticidade E do material do corpo de prova.

Feito isso, vamos poder encontrar a deformação final no corpo ε p = ε - σ / E , e, em seguida, encontrar o comprimento final L ' = L ( 1 + ε p ) .

Passo 2

Começando pela determinação do módulo de elasticidade E do material do corpo de prova!

Da Lei de Hooke σ = E ε , temos que:

E = σ ε

Sendo assim, podemos escolher um ponto da região do Diagrama Tensão-Deformação do material que segue a Lei de Hooke:

E utilizar os valores de σ e ε nesse ponto para calcular E :

E = ( 14   M P a ) ( 0,004   m m / m m )

⇓

E = 3500   M P a

Passo 3

Agora que sabemos o módulo de elasticidade E do material, já podemos calcular a deformação final ε p :

ε p = ε - σ E

Substituindo a deformação atingida ε = 0,024   m m / m m , a tensão atingida σ = 26   M P a e o módulo de elasticidade E = 3500   M P a , temos:

ε p = 0,024 - 26   M P a 3500   M P a

Calculando isso, encontramos que:

ε p = 0,0165714   m m / m m

Passo 4

Por fim, podemos calcular o comprimento final L ' do corpo de prova:

L ' = L ( 1 + ε p )

Substituindo os valores L = 250   m m e ε p = 0,0165714   m m / m m , isso fica assim:

L ' = ( 250   m m ) ( 1 + 0,0165714 )

O que dá:

Resposta

L ' = 254,143   m m

Exercício Resolvido #4

Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 72-3.21.

A figura apresenta o diagrama tensão-deformação para uma resina de poliéster. Se a viga for suportada por uma barra A B e um poste C D , ambos feitos desse material, e for submetida à carga P = 80   k N , determine o ângulo de inclinação da viga quando a carga for aplicada. O diâmetro da barra é 40   m m , e o diâmetro do poste é 80   m m .

Passo 1

O que está acontecendo?

A barra A B e o poste C D estão contribuindo para o equilíbrio da viga A C através de forças F A B e F C D :

Aplicando as condições de equilíbrio para essa viga, conseguimos encontrar as forças F A B e F C D em função da carga P = 80   k N .

Mas pelo princípio da ação e reação, se a barra e o poste fazem essas forças na viga, a viga var reagir com forças contrárias na barra e no poste:

A força F A B de tração na barra A B vai gerar nela uma força interna normal N A B = F A B , enquanto que a força F C D   de compressão no poste C D vai gerar nele uma força interna normal N C D = - F C D .

Pessoal, se lembrem que a normal é negativa quando há compressão e positiva quando há tração.

Como uma consequência desse carregamento, a barra e o poste vão sofrer, respectivamente, variações de comprimento δ A B e δ C D , que vão poder ser calculadas através da fórmula

δ = N L E A

Sendo que:

  • Os comprimentos dessas peças são L A B = 2   m , para a barra, e L C D = 0,5   m , para o poste;
  • As duas peças vão ter o mesmo módulo de elasticidade E , que pode ser encontrado a partir do Diagrama Tensão-Deformação fornecido;
  • E as áreas A das seções transversais dessas peças podem ser calculadas a partir de seus diâmetros, d A B = 40   m m e d C D = 80   m m , usando a fórmula A = π d 2 / 4 .

E o que é que o exercício quer?

Ele quer que a gente descubra qual vai ser o ângulo de inclinação que a viga A C vai ganhar por causa das deformações/variações de comprimento na barra e no poste.

Agora, para analisar esse ângulo, vamos ter que encontrar primeiro as variações de comprimento δ A B e δ C D .

Então vamos começar o exercício determinando os valores do módulo de elasticidade E e das forças normais N A B na barra e N C D no poste, para que depois a gente possa usar a fórmula δ = N L / E A .

Passo 2

Para encontrar o módulo de elasticidade E do material, vamos recorrer a Lei de Hooke:

σ = E ε

Isolando E , temos que:

E = σ ε

Então para calcular E , precisamos de um par de valores para a tensão σ e a deformação ε que sigam a Lei de Hooke, o que é seguir a lei de Hooke? Isso significa que esses dois valores devem estar dentro na porção reta do diagrama (onde há deformação elástica).

Olhando para o Diagrama Tensão-Deformação do material, um par de valores desses já está marcado:

Usando esses valores, vamos ter que:

E = ( 32,2   M P a ) ( 0,01   m m / m m )

O que dá:

E = 3220   M P a

Ou, se preferirmos:

E = 3,22   G P a

Passo 3

Já para encontrar as forças internas normais N na barra e no poste, vamos primeiro fazer o diagrama de corpo livre da viga para encontrar as forças F A B e F C D em função da carga P :

Aqui, podemos aplicar duas condições de equilíbrio: o equilíbrio de momentos e o equilíbrio de forças na vertical.

Pessoal, as forças F A B e F C D podem ser achadas por simetria e cada uma tem módulo igual à metade da força P :

F A B = F C D = P 2

Por fim, como vimos no primeiro passo, temos que N A B = F A B e que N C D = - F C D .

Dessa forma, encontramos que:

N A B = P 2       &       N C D = - P 2

Passo 4

Agora que já encontramos o módulo de elasticidade E e as forças normais N , já temos todas as informações necessárias para calcular as variações de comprimento δ na barra e no poste. Visualizando esse efeito vamos ter:

Aplicando a fórmula δ = N L / E A para a barra A B e para o poste C D , temos:

δ A B = N A B L A B E A A B       &       δ C D = N C D L C D E A C D

Podemos definir as áreas A de seção transversal da barra e do poste a partir de seus diâmetros d A B e d C D usando a fórmula A = π d 2 / 4 .

Além disso, temos que N A B = P / 2 e N C D = - P / 2 .

Fazendo essas substituições, temos que:

δ A B = P 2 L A B E π d A B 2 4       &       δ C D = - P 2 L C D E π d C D 2 4

Arrumando essas equações, elas ficam assim:

δ A B = 2 P L A B E π d A B 2       &       δ C D = - 2 P L C D E π d C D 2

Agora só falta substituir os valores de P = 80   k N e E = 3,22   G P a , além dos comprimentos e diâmetros da barra e do poste.

Fazendo essas substituições, temos:

δ A B = 2 80   k N 2   m 3,22   G P a π 40   m m 2       &       δ C D = - 2 80   k N 0,5   m 3,22   G P a π 80   m m 2

Para as duas contas, temos que G P a = k N / m m 2 , de tal forma que as unidades “ k N ” e “ m m 2 ” vão se cortar e o resultado final vai sair em m .

Calculando tudo, encontramos:

δ A B = 0,0197708   m       &       δ C D = - 0,0012357   m

Reescrevendo esses resultados em m m , temos:

δ A B = 19,7708   m m       &       δ C D = - 1,2357   m m

Passo 5

Pronto, agora que já conhecemos as variação de comprimento na barra e no poste, só nos resta avaliar a nova inclinação da viga A C .

De um lado, temos que a barra vai se esticar 19,7708   m m , de tal forma que o ponto A da viga vai descer essa distância.

Do outro, temos que o poste vai se comprimir 1,2357   m m , fazendo o ponto C da viga descer essa distância.

Dessa forma, a disposição final A ' C ' da viga vai ficar assim:

A tangente do ângulo α de inclinação vai ser igual ao cateto oposto (igual à diferença entre 19,7708   m m e 1,2357   m m ) dividido pelo adjacente (igual ao comprimento de 1500   m m da viga):

t g   α = 19,7708   m m - 1,2357   m m 1500   m m

O que dá:

t g   α = 0,0123567

Por fim, usando a função t g - 1 ou a r c t g da nossa calculadora, encontramos nossa resposta:

α = 0,708 °

Resposta

α = 0,708 °

Exercício Resolvido #5

Elaboração própria

Com base no gráfico de tensão e deformação dado abaixo, responda se as alternativas são falsas ou verdadeiras, justificando aquelas que são falsas.

  1. ( ) O modulo de elasticidade do material A é maior que o modulo de elasticidade do material B
  2. ( ) A resistência a tração do material B é maior que o de A
  3. ( ) Os gráficos parecem demonstrar que ambos os materiais são frágeis
  4. ( ) Os matérias A e B rompem na mesma deformação, apesar de possuírem tensões de rompimento diferentes.

Passo 1

Para fazer essa questão temos que analisar cada numa das alternativas cuidadosamente.

  1. ( ) O modulo de elasticidade do material A é maior que o modulo de elasticidade do material B

    2. Sabemos que o modulo de elasticidade é obtido dividindo-se a tensão pela deformação especifica, ou seja, é a inclinação do nosso gráfico. Como se trata da tangente, quanto maior a inclinação maior o modulo de elasticidade, analisando os gráficos teremos que

    A inclinação de A é maior que a de B, logo o modulo de elasticidade de A é maior que o de B. alternativa verdadeira.

    Passo 2

  2. ( ) A resistência a tração do material B é maior que o de A

    3. A resistência a tração é marcada pelo ponto máximo alcançado pelo gráfico, analisando então os gráficos teremos que

    Nesse caso vemos que a resistência a tração é maior no material A do que no B. logo, a alternativa é falsa.

    Passo 3

  3. ( ) Os gráficos parecem demonstrar que ambos os materiais são frágeis

    4. Matérias frágeis apresentam ruptura bruta, ou seja, geralmente não entram no regime plástico, passando do regime elástico diretamente para a ruptura. Analisando os gráficos teremos que

    Vemos marcados em azul os trechos de regime plástico que cada material entrou logo após sair o regime elástico, vindo logo após a ruptura. Ou seja, esses gráficos possuem maior probabilidade de representarem materiais dúcteis do que frágeis. Logo a alternativa é falsa.

    Passo 4

  4. ( ) Os matérias A e B rompem na mesma deformação, apesar de possuírem tensões de rompimento diferentes.

sabemos que o rompimento se trata da parte mais extrema do gráfico, no caso a alternativa diz que rompem na mesma deformação, porém em tensões diferentes.

Analisando o gráfico teremos que

De fato ambos os matérias rompem a tensões diferentes, mas a s deformações não são iguais, logo a alternativa também é falsa.

Resposta

  1. ( V ) O modulo de elasticidade do material A é maior que o modulo de elasticidade do material B
  2. ( F ) A resistência a tração do material B é maior que o de A
  3. ( F ) Os gráficos parecem demonstrar que ambos os materiais são frágeis
  4. ( F ) Os matérias A e B rompem na mesma deformação, apesar de possuírem tensões de rompimento diferentes.

Exercício Resolvido #6

Elaboração própria

Com base no gráfico de tensão e deformação dado abaixo, responda se as alternativas são falsas ou verdadeiras, justificando aquelas que são falsas.

  1. ( ) O modulo de elasticidade do material A é maior que o modulo de elasticidade do material B, porém é menor que o de C.
  2. ( ) O modulo de resistência a tração do material C é maior que o do material B
  3. ( ) O modulo tensão de ruptura de todos os matérias são iguais
  4. ( ) Os gráficos parecem demonstrar que os matérias C e B são dúcteis e o material A é frágil.
  5. ( ) Os matérias A, B e C rompem aproximadamente na mesma deformação, apesar de possuírem tensões de rompimento diferentes.

Passo 1

Para fazer essa questão temos que analisar cada numa das alternativas cuidadosamente.

  1. ( ) O modulo de elasticidade do material A é maior que o modulo de elasticidade do material B, porém é menor que o de C.

    2. Sabemos que o modulo de elasticidade é obtido dividindo-se a tensão pela deformação especifica, ou seja, é a inclinação do nosso gráfico. Como se trata da tangente, quanto maior a inclinação maior o modulo de elasticidade, analisando os gráficos teremos que

    Vemos que a maior inclinação é da curva B, logo em seguida da curva C e por fim da curva A, ou seja, a alternativa é falsa pois a curva A possui o menor modulo de elasticidade.

    Passo 2

  2. ( ) O modulo de resistência a tração do material C é maior que o do material B

    3. A resistência a tração é marcada pelo ponto máximo alcançado pelo gráfico, analisando então os gráficos teremos que

    Apesar da sutil diferença vemos que a reação a tração do material C é maior que a do material B, logo a alternativa é verdadeira.

    Passo 3

  3. ( ) O modulo tensão de ruptura de todos os matérias são iguais

    4. sabemos que o rompimento se trata da parte mais extrema do gráfico, no caso a alternativa diz que rompem na mesma tensão de ruptura.

    Analisando o gráfico teremos que

    Podemos ver que os matérias B e C possuem uma diferença sutil, mas o material A rompe em uma tensão completamente diferente, ou seja, alternativa falsa.

    Passo 4

  4. ( ) Os gráficos parecem demonstrar que os matérias C e B são dúcteis e o material A é frágil.

    5. Matérias frágeis apresentam ruptura bruta, ou seja, geralmente não entram no regime plástico, passando do regime elástico diretamente para a ruptura, matérias dúcteis apresentam região plástica bem definida antes da ruptura do material. Analisando os gráficos teremos que

    A região azul nos gráficos B e C representam uma região de transição entre o regime elástico e a ruptura, que é exatamente o regime plástico em que ocorre a estricção do material, características pertinentes aos matérias dúcteis. Já o material A apresenta uma ruptura brusca, sem a presença do regime plástico, de fato demonstrando as características de um material frágil. Logo a alternativa é verdadeira.

    Passo 5

  5. ( ) Os matérias A, B e C rompem aproximadamente na mesma deformação, apesar de possuírem tensões de rompimento diferentes.

sabemos que o rompimento se trata da parte mais extrema do gráfico, no caso a alternativa diz que rompem na mesma deformação, porém em tensões diferentes.

Analisando o gráfico teremos que

De fato os materiais A, B e C possuem deformações muito próximas quando estão na ruptura, apesar de cada material possuir tensões de ruptura diferentes entre si. Logo a alternativa também é verdadeira.

Resposta

  1. ( F ) O modulo de elasticidade do material A é maior que o modulo de elasticidade do material B, porém é menor que o de C.
  2. ( V ) O modulo de resistência a tração do material C é maior que o do material B
  3. ( F ) O modulo tensão de ruptura de todos os matérias são iguais
  4. ( V ) Os gráficos parecem demonstrar que os matérias C e B são dúcteis e o material A é frágil.
  5. ( V ) Os matérias A, B e C rompem aproximadamente na mesma deformação, apesar de possuírem tensões de rompimento diferentes.

Exercício Resolvido #7

Elaboração própria

Com base no gráfico de tensão e deformação dado abaixo, responda se as alternativas são falsas ou verdadeiras, justificando aquelas que são falsas.

  1. ( ) O material B apresenta deformações residuais
  2. ( ) Todos os materiais rompem na mesma tensão de ruptura
  3. ( ) Os gráficos parecem demonstrar que os materiais C e B são dúcteis e o material A e D são frágeis.
  4. ( ) O Modulo de elasticidade das curvas B e A são iguais.
  5. ( ) A zona de estricção é atingida primeiro pelo material D
  6. ( ) A tensão máxima é atingida primeiro pelo material B por apresentar maiores deformações
  7. ( ) Um desses gráfico poderia representar facilmente o comportamento do aço

Passo 1

Para fazer essa questão temos que analisar cada numa das alternativas cuidadosamente

  1. ( ) O material B apresenta deformações residuais

    2. Para sabermos se um material apresenta tensões residuais, precisamos analisar se o material apresenta deformações quando as tensões aplicadas sobre ele são zero. Se não apresentar significa que não há deformações residuais. Se apresentar significa que esse material já foi carregado uma vez, atingiu o regime plástico e foi descarregado, com esse descarregamento recuperou toda deformação elástica, mas a deformação plástica se tornou permanente, essa deformação permanente que chamaremos de deformação residual, analisando o gráfico teremos que

    Vemos que de fato o material B apresenta deformações residuais, logo a nossa alternativa é verdadeira.

    Passo 2

  2. ( ) Todos os materiais rompem na mesma tensão de ruptura

    3. sabemos que o rompimento se trata da parte mais extrema do gráfico, no caso a alternativa diz que rompem na mesma tensão de ruptura.

    Analisando o gráfico teremos que

    De fato todos os matérias rompem na mesma tensão de ruptura. Até mesmo o material B que possui tensões residuais e deformações maiores romperá na mesma tensão de rupruta dos outros matérias.

    Passo 3

  3. ( ) Os gráficos parecem demonstrar que os matérias C e B são dúcteis e o material A e D são frágeis.

    4. Matérias frágeis apresentam ruptura bruta, ou seja, geralmente não entram no regime plástico, passando do regime elástico diretamente para a ruptura, matérias dúcteis apresentam região plástica bem definida antes da ruptura do material. Analisando os gráficos teremos que

    Vemos pelos gráficos com cores azuis claras marcando a transição do regime elástico para a ruptura que se tratam de matérias dúcteis, exatamente por possuírem região de regimes plásticos. Vemos também que o material C apresenta ruptura brusca sem transição do regime elástico para a ruptura, caracterizando assim um material frágil. Logo vemos facilmente que a alternativa é falsa.

    Passo 4

  4. ( ) O Modulo de elasticidade das curvas B e A são iguais.

    5. Para que o modulo de elasticidade entre as curvas A e B sejam iguais, será necessário avaliar se as inclinações de ambos os gráficos são iguais, se a inclinação for igual por consequência o modulo de elasticidade também será, analisando o gráfico teremos que

    Como as curvas são praticamente paralelas e as suas inclinações são muito próximas, podemos dizer que de fato os módulos de elasticidade dos matérias A e B são iguais. Logo essa alternativa também está correta.

    Passo 5

  5. ( ) A zona de estricção é atingida primeiro pelo material D

    6. É importante entender que zona de estricção é a zona compreendida entre a resistência máxima a tração e a ruptura da peça, ou seja, se desejamos saber qual material atinge primeiro a zona de estricção, devemos descobrir qual material atinge primeiro o máximo da resistência a tração, analisando o gráfico vemos que

    Vemos que o material que primeiro atinge o máximo é o material D, logo ele atingira a zona de estricção primeiro que os outro materiais. Alternativa verdadeira.

    Passo 6

  6. ( ) A tensão máxima é atingida primeiro pelo material B por apresentar maiores deformações

    7. Usando a mesma análise feita anteriormente concluímos que o primeiro material a atingir a tensão máxima foi o material D. logo alternativa falsa.

    Passo 7

  7. ( ) Um desses gráfico poderia representar facilmente o comportamento do aço

Sabemos que o gráfico que melhor representa o comportamento do aço é

Comparando com os gráficos temos que

Nenhuma curva de fato se parece com o comportamento do aço, logo alternativa falsa.

Resposta

  1. ( V ) O material B apresenta deformações residuais
  2. ( V ) Todos os materiais rompem na mesma tensão de ruptura
  3. ( F ) Os gráficos parecem demonstrar que os matérias C e B são dúcteis e o material A e D são frágeis.
  4. ( V ) O Modulo de elasticidade das curvas B e A são iguais.
  5. ( V ) A zona de estricção é atingida primeiro pelo material D
  6. ( F ) A tensão máxima é atingida primeiro pelo material B por apresentar maiores deformações
  7. ( F ) Um desses gráfico poderia representar facilmente o comportamento do aço

Exercícios de Livros Relacionados

A figura apresenta o diagrama tensão-deformação para um aço-liga com 12m m de diâmetro original e comprimento de referência 50m m . Determine os valores aproximados do módulo de elasticidade para o ma
O diagrama tensão-deformação para o polietileno que é utilizado para revestir cabos coaxiais é determinado por um ensaio com um corpo de prova com comprimento de referência de 250m m . Se uma carga P
A figura apresenta o diagrama tensão-deformação para um aço-liga com 12m m de diâmetro original e 50m m de comprimento de referência. Determine os valores aproximados do módulo de resiliência e do mód
A figura mostra a porção elástica do diagrama tensão-deformação para uma liga de alumínio. O corpo de prova usado para o ensaio tem comprimento de referência de 50m m e 12,5m m de diâmetro. Quando a c
Um corpo de prova de aço com diâmetro original de 13m m e 50m m de comprimento de referência foi submetida a um ensaio de tração. Os dados resultantes são apresentados na tabela. Construa o gráfico do