Energia de Deformação
Produzido por Pablo RicardoTeoria
Introdução
Se lembra como, lá na física, uma mola deformada tinha uma certa energia potencial elástica?
Isso acontecia porque, para deformar a mola, você tinha que realizar um trabalho nela, e esse trabalho era absorvido na forma da energia elástica.
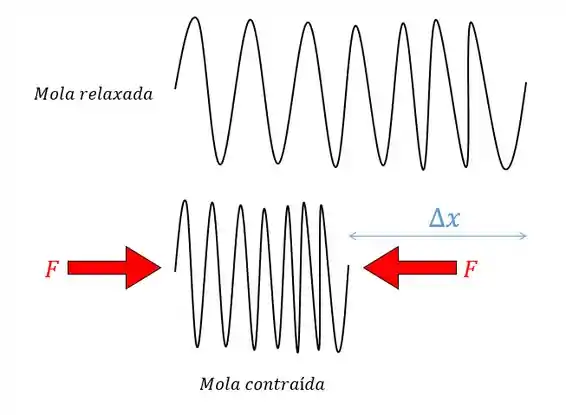
Então...
Da mesma forma, qualquer peça que estiver deformada elasticamente (de acordo com a Lei de Hooke) vai ter uma certa Energia de Deformação dada pela fórmula:
Onde é a tensão na peça, a deformação e é o volume inicial da peça. Observe que somente podemos utilizar esse conceito quando a deformação é elástica, ou seja, não causa deformação permanente na peça. Vamos fazer um exemplo prático desse cálculo.
Calcule a energia de deformação quando uma peça cilíndrica de diâmetro da base e altura sofre um alongamento de . Sabe-se que a força normal aplicada à essa peça vale .
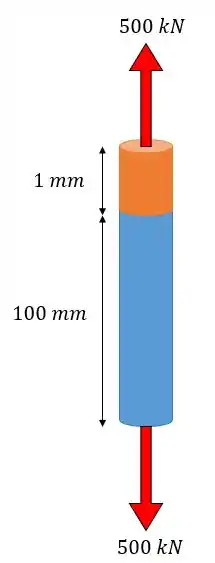
Resolução: Para resolver essa questão basta que achemos a tensão normal, a deformação e o volume da peça e substituir na fórmula.
A tensão é dada pela força sobre a área:
A deformação é um adimensional que é dado pelo alongamento sobre o tamanho inicial:
E o volume inicial da peça é dado por:
Agora é só substituir na equação:
Densidade da Energia de Deformação
Talvez, ao invés da energia de deformação , pode ser pedido para você calcular a densidade de energia de deformação em um material, que vai ser dada por:
Dessa forma, temos que a energia de deformação de uma peça vai ser a densidade multiplicada pelo volume da peça.
Então para o caso calculado anteriormente nós teríamos uma densidade da energia de deformação de:
Módulo de Resiliência
O que é resiliência para você? Essa palavra está muito em foco hoje em dia não é mesmo? Sempre escutamos falar da resiliência das pessoas. Resiliência é a capacidade que alguém tem de apanhar e apanhar e permanecer na luta, inalterado. O Rocky é um cara resiliente.

Para os materiais nós vamos ter mais ou menos a mesma coisa. Um material resiliente é aquele que se deforma muito e ainda volta ao normal. Isso acontece por exemplo com o arco do arqueiros, esse objeto tem que estar suscetível apenas à deformação elástica e não à plástica. Por exemplo o bambu, material dos arcos japoneses. Olha esse tiozinho testando a resiliência do bambu.

Legal né? Mas como vamos calcular de fato a resiliência? As fórmulas que vimos para e supõem que os materiais se deformaram de acordo com a Lei de Hooke.
Mas acontece que muitos materiais deixam de seguir a Lei de Hooke a partir de um certo nível de tensão, chamado de limite de proporcionalidade.
Daí que se a gente fosse calcular o valor máximo de que um material pode ter sem deixar de seguir a Lei de Hooke, esse valor seria o módulo de resiliência do material:
Perceba que trata-se da energia acumulada pelo material exatamente no ponto limite de proporcionalidade!
Onde e são os valores da tensão e da deformação no limite de proporcionalidade do material.
OBS: Limite de proporcionalidade não significa que saímos do regime elástico para o plástico, significa apenas que o nosso gráfico não é mais uma reta fica ligado nisso!
Além desse cálculo utilizando o limite de proporcionalidade, podemos calcular o módulo de resiliência de um material usando o Diagrama Tensão-Deformação desse material.
Nesse caso, vai ser igual a área triangular que está abaixo da parte do diagrama que segue a Lei de Hooke:
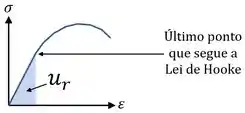
Olha como essa área é um triângulo e é igualzinha à nossa equação:
Módulo de Tenacidade
Já o módulo de tenacidade é a densidade de energia de deformação máxima que um material pode adquirir antes dele se romper.
Ele é igual a área debaixo de todo o Diagrama Tensão-Deformação do material e é calculado somando a área de trapézios, retângulos e triângulos que aproximem a curva do diagrama, ou fazendo a integral.
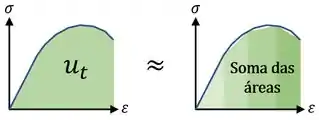
Mas pessoal, muito provavelmente vocês não vão realizar esses cálculos. O que será cobrado de vocês será comparar dois diagramas e dizer qual material é mais tenaz, por exemplo:
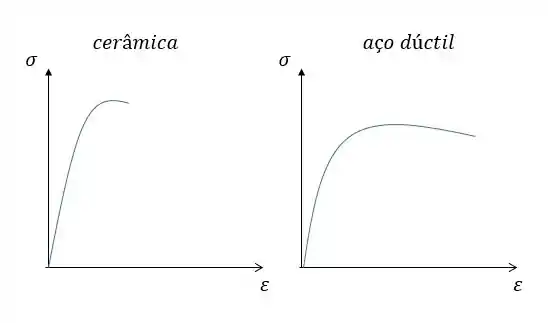
E aí, qual dos dois parece ser mais tenaz?
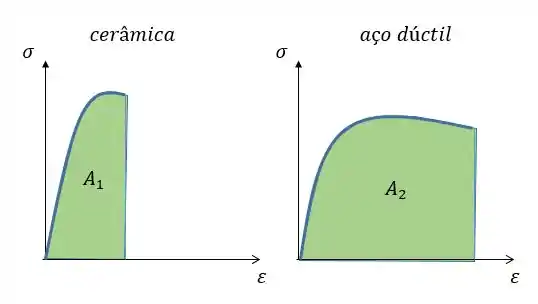
A área do aço dúctil parece ser bem maior não é mesmo? Então ele é mais tenaz!
Densidade da Energia de Deformação
Módulo de Resiliência
Módulo de Tenacidade
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Uma coluna de concreto com uma seção transversal de está submetida a uma compressão de .
Considerando que, nessas condições, o concreto possui um comportamento elástico-linear, determine a densidade de energia de deformação no concreto.
Dados:
Passo 1
A coluna de concreto possui uma área de seção transversal e um módulo e elasticidade .
Além disso, como a única força na coluna é a compressão de , vamos ter na coluna uma força interna normal .
E o que é que o exercício quer?
Ele quer saber a densidade de energia de deformação na coluna.
Como o concreto possui um comportamento elástico-linear (está seguindo a Lei de Hooke), temos que vai ser dado pela fórmula:
Nessa fórmula, podemos usar a Lei de Hooke para substituir a deformação e a fórmula da tensão normal média para substituir a tensão .
Dessa forma, vamos encontrar uma expressão para em função de valores que conhecemos!
Passo 2
Então, vamos começar aplicando a fórmula da densidade de energia de deformação para um material que está seguindo a Lei de Hooke:
Da Lei de Hooke , temos que .
Fazendo essa substituição, encontramos que:
Em seguida, aplicando a fórmula da tensão normal média, temos que:
E pronto! Temos uma expressão para em função de valores que conhecemos!
Passo 3
Substituindo os valores de , e na expressão anterior, temos:
A parte dessa equação que está elevada ao quadrado tem unidades , que é o mesmo que .
Dessa forma, vamos ter como unidade na parte superior da equação enquanto que já temos como unidade na parte inferior.
Sendo assim, o resultado da conta vai sair em !
Calculando tudo, encontramos que:
Esse número é bastante pequeno, então podemos reescrevê-lo em :
Passo 4
Poderiamos terminar o exercício por aqui.
Mas ainda temos uma coisa para fazer: como é uma medida de densidade de energia, queremos dar o resultado de em uma unidade de energia sobre volume.
(A unidade atual do nosso resultado para é , que é uma unidade de tensão!)
Então vamos pensar...
Multiplicando em cima e em baixo por , isso fica assim:
Mas é o mesmo que joule, então:
Sendo assim, podemos reescrever o nosso resultado, que está em , em :
E assim temos a nossa resposta:
Resposta
Exercício Resolvido #2
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 68-3.2.
Os dados obtidos em um ensaio de tensão-deformação para um material cerâmico são dados na tabela. A curva é linear entre a origem e o primeiro ponto. Represente o diagrama em gráfico e determine o módulo de elasticidade e o módulo de resiliência.
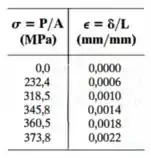
Passo 1
A primeira coisa que fazemos nesse exercício é desenhar o Diagrama Tensão-Deformação do material em um gráfico:
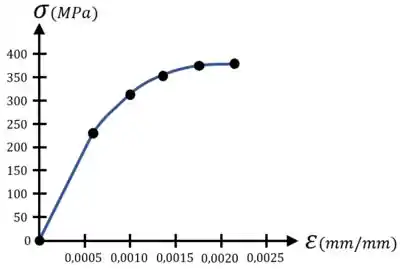
Em seguida, o exercício quer que a gente determine o módulo de elasticidade e o módulo de resiliência desse material.
Para tanto, vamos usar a informação de que a curva é linear entre a origem e o primeiro ponto.
O que isso significa é que o primeiro ponto é o limite de proporcionalidade do material (o último ponto do diagrama que segue a Lei de Hooke), de tal forma que:
Agora, lembra aí!
Para calcular o módulo de elasticidade de um material, podemos usar os valores de e de qualquer ponto do diagrama tensão-deformação que siga a Lei de Hooke .
Usando e , vamos ter que:
O que significa que:
E para calcular o módulo de resiliência do nosso material, podemos nos lembrar que ele é igual à área triangular debaixo da região linear do diagrama tensão-deformação:
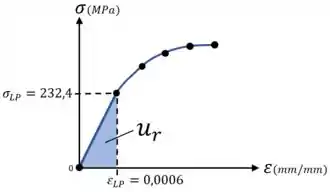
Ou podemos nos lembrar diretamente da fórmula para :
Passo 2
Agora que já desenhamos o Diagrama Tensão-Deformação do material e entendemos como encontrar os valores de e para o material, vamos calcular esses valores!
Para o módulo de elasticidade , temos que:
Substituindo os valores de e , encontramos que:
O que dá:
Como esse número é um pouco grande, o reescrevemos em :
E para o módulo de resiliência , temos que:
Substituindo os valores de e , encontramos:
Calculando, isso dá:
Passo 3
Poderiamos já terminar o exercício por aqui.
Mas temos mais uma coisa que podemos fazer: como é uma medida de densidade de energia, queremos dar o resultado de em uma unidade de energia sobre volume.
(A unidade atual do nosso resultado para é , que é uma unidade de tensão!)
Então vamos pensar...
Multiplicando em cima e em baixo por , isso fica assim:
Mas é o mesmo que joule, então:
Sendo assim, podemos reescrever o nosso resultado, que está em , em :
E assim, finalizamos o exercício:
Resposta
Exercício Resolvido #3
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 68-3.3.
Os dados obtidos em um ensaio de tensão-deformação para um material cerâmico são dados na tabela. A curva é linear entre a origem e o primeiro ponto. Represente o diagrama em gráfico e determine o valor aproximado do módulo de tenacidade. A tensão de ruptura é .
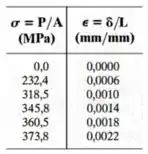
Dica do Expert: Se você fez o exercício passado, o gráfico é o mesmo!
Passo 1
O primeiro passo desse exercício é desenhar o gráfico, que vai ser o mesmo do exercício passado, caso você já tenha feito ele:
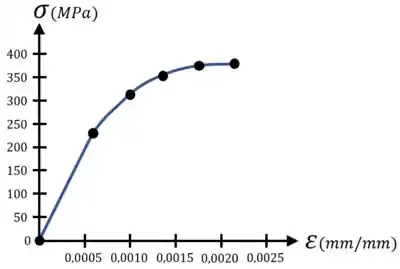
Passo 2
Agora, em seguida, o exercício quer que a gente calcule o módulo de tenacidade do material.
Lembra aí!
Para calcular isso, vamos ter que calcular a área debaixo de todo o gráfico do diagrama tensão-deformação desse material:
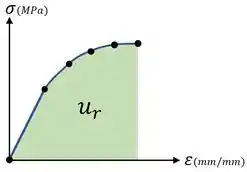
E, para calcular essa área, vamos ter que aproximar ela como a soma das áreas de uma série de triângulos, retângulos e trapézios que aproximam essa curva.
A gente pode escolher dividir essa área como quiser! Só devemos evitar ignorar algum pedaço grande de área.
Para obter o mesmo gabarito do livro, dividimos essa área assim:
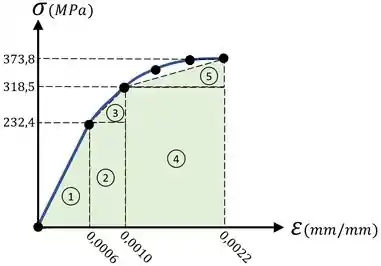
De tal forma que vai ser a soma das áreas das regiões a :
Observando o gráfico, calculamos essas áreas individuais assim:
Finalmente, calculando tudo isso, encontramos que:
Resposta
(O seu resultado pode ser maior ou menor, já que o cálculo de é aproximado.)
Exercício Resolvido #4
Elaboração Própria
Um eixo de aço de volume foi tracionado até uma tensão e uma deformação .
Considerando que o eixo está se comportando de forma linear-elástica, determine a energia de deformação nesse eixo.
Passo 1
A energia de deformação em uma peça que está seguindo a Lei de Hooke (ou seja, que está se comportando de forma linear-elástica), é dada pela fórmula:
Substituindo os valores de , e , temos que:
Como é o mesmo que , o resultado dessa conta vai sair em .
Calculando tudo, encontramos que:
Substituindo por , vamos ter que:
Finalmente, substituindo por joule (), encontramos nossa resposta:
Resposta
Exercício Resolvido #5
Elaboração Própria
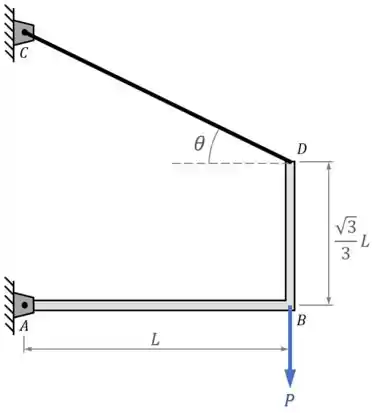
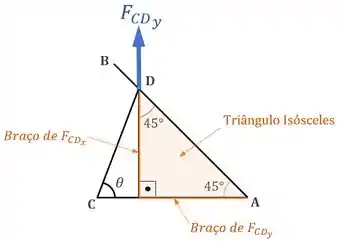
A estrutura abaixo suporta um peso em sua ponta e é sustentada pelo cabo de aço , que forma um ângulo com a horizontal. Considerando que o cabo de aço possuí uma área de seção transversal e que ele se comporta de acordo com a Lei de Hooke, possuindo um módulo de elasticidade , determine:
a força de tração no cabo em função do ângulo ;
o valor de para o qual a força é mínima;
& a densidade de energia de deformação no cabo quando é mínima.
Passo 1
O que está acontecendo?
A estrutura traciona o cabo de aço com uma força .
O cabo reage a essa tração fazendo uma força de mesma intensidade que contribui para o equilíbrio da estrutura, como mostra o Diagrama de Corpo Livre da estrutura:
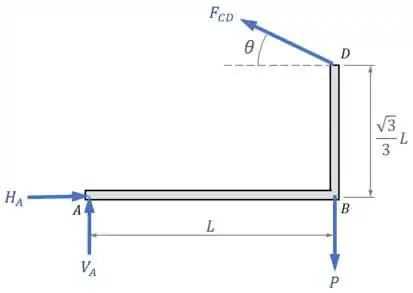
Aplicando as condições de equilíbrio nessa estrutura , é possível encontrar uma expressão para a força em função do peso e do ângulo , respondendo assim o item .
Em seguida, para responder o item , vamos ter que usar a propriedade que vimos em cálculo que diz que os máximos e mínimos de uma função ocorrem quando a sua derivada é igual a zero.
Por fim, para resolver o item , vamos ter que utilizar o valor encontrado para no item anterior para encontrar a força mínima.
Com isso, vamos poder calcular a tensão normal média no cabo de aço, e, em seguida, calcular a densidade de energia de deformação .
Passo 2
Começando pelo item :
Para encontrar a força em função do ângulo , vamos ter que observar o Diagrama de Corpo Livre da estrutura :
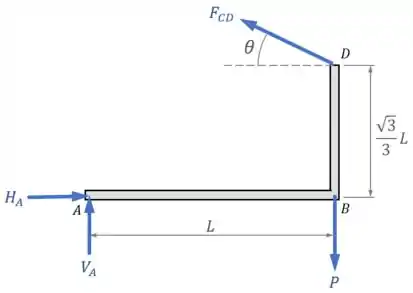
E aplicar as condições de equilíbrio para essa estrutura.
Então vamos pensar...
A condição de equilíbrio que nos permite encontrar sem que a gente tenha que se preocupar em calcular as reações no apoio em ( e ) vai ser o equilíbrio de momentos em relação ao ponto :
Em relação ao ponto , já conseguimos ver que o peso vai gerar um momento no sentido horário () com um braço .
Quanto a força , fica difícil visualizar o braço do momento que ela vai gerar uma vez que ela é uma força inclinada.
Para facilitar nossa vida, podemos decompor em uma componente horizontal e uma componente vertical :
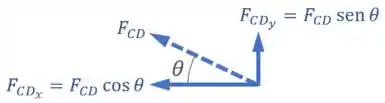
Pensando assim, vamos ter que, em relação ao ponto :
- A força vai gerar um momento no sentido anti-horário () com um braço ;
- E a força vai gerar outro momento no sentido anti-horário (), mas com um braço .
Agora que entendemos como vão ficar os momentos em relação ao ponto , podemos fazer o somatório de momentos, que fica assim:
Dividindo tudo por e passando para o outro lado, temos que:
Substituindo e :
Tirando em evidência:
Finalmente, isolando encontramos que:
E assim está resolvido o item !
Passo 3
Agora, no item , temos que analisar para qual valor de a força abaixo vai ser mínima:
Bom, essa força vai ser mínima quando a expressão “” que está dividindo ela for máxima.
Agora, lá em cálculo nós vimos que os máximos e mínimos das funções ocorrem quando as suas derivadas são iguais à zero.
Então vamos aplicar essa condição da derivada igual a zero aqui e descobrir qual é o valor de que satisfaz ela:
Sabendo que derivada de seno é cosseno e que derivada de cosseno é menos seno, essa derivada fica assim:
Passando para o outro lado, temos que:
Dividindo tudo por , encontramos que:
O que significa que:
O ângulo que possui tangente igual à é o ângulo de , então temos que:
Ou seja, podemos dizer que a força é mínima quando !
Passo 4
Finalmente, para o item , vamos precisar da tensão normal média no cabo de aço para podermos encontrar a densidade de energia de deformação .
Para encontrar , vamos primeiro encontrar o valor da força mínima, e, em seguida, encontrar a tensão normal média correspondente.
Aplicando a fórmula que encontramos para no item , temos que:
Substituindo :
Como e :
Simplificando essa expressão, ela fica assim:
Ou seja:
Simplificando mais uma vez, finalmente encontramos que:
Ou seja, a força mínima no cabo de aço ocorre quando e é igual a .
Além disso, como a força é a força de tração no cabo, vamos ter que a força interna normal no cabo vai ser igual a , ou seja:
E essa força normal vai gerar uma tensão normal média no cabo de aço:
Passo 5
Agora que conhecemos o valor da tensão normal média no cabo quando a força é mínima, podemos calcular a densidade de energia de deformação no cabo nesse caso.
Da fórmula da densidade de energia de deformação , temos que:
Nós não conhecemos a deformação no cabo, mas sabemos que o cabo está seguindo a Lei de Hooke , de tal forma que:
Fazendo essa substituição na fórmula de , encontramos que:
Substituindo o valor encontrado para a tensão normal média :
O que nos dá a resposta para o item :
Resposta
Exercício Resolvido #6
Prova 1 - 2016.1 - Prof. Roberto - Resistência dos Materiais 1 - UFRJ
Uma barra rígida de comprimento e peso é mantida a apoiada em uma escora de comprimento . A escora é posicionada de modo a receber a menor força de compressão possível. Desprezar o peso da escora e supor que , e funcionem como apoios simples. Calcular:
o ângulo para o qual a força na escora é mínima;
a força mínima;
a área da seção transversal da escora, sendo a tensão admissível do material da mesma;
o encurtamento da escora;
a energia de deformação acumulada.
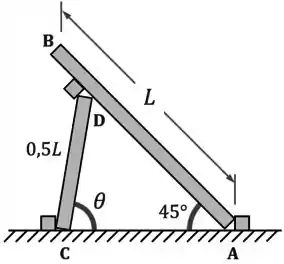
Dica do Expert: Em um momento desse exercício, pode ser útil lembrar que e que . (Essas duas fórmulas vêm das fórmulas para seno e cosseno de .)
Passo 1
O que está acontecendo?
O momento gerado pelo peso da barra rígida é equilibrado pelo momento gerado pela força que a escora faz na barra:
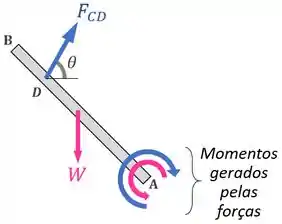
Daí que, pelo princípio da ação e reação, a barra vai reagir à força feita nela pela escora com uma força de compressão na escora de mesma intensidade :
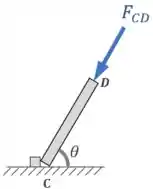
E o que é que o exercício quer?
Nos itens e , o exercício quer que a gente analise essa força , para que depois, a gente use ela para calcular outros valores nos itens , e .
Daí que o grande desafio desse exercício é encontrar uma expressão para a força .
Para fazer isso, vamos ter que aplicar as condições de equilíbrio na barra , o que vai nos dar um tanto de trabalho uma vez que o braço e a direção de dependem do ângulo .
Depois que tivermos uma expressão para , vamos poder prosseguir, item por item, fornecendo as respostas do exercício!
Passo 2
Então, vamos começar aplicando as condições de equilíbrio na barra !
Fazendo um diagrama de corpo livre dela, temos as seguintes forças:
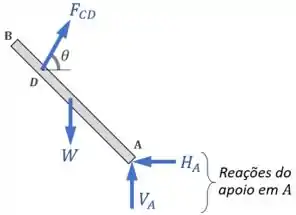
A condição de equilíbrio que vai nos permitir encontrar uma expressão para a força mais facilmente vai ser o equilíbrio de momentos em relação ao ponto :
Agora, calcular o momento da força inclinada é um tanto complicado, então vamos decompor ela em uma componente horizontal e uma componente vertical :
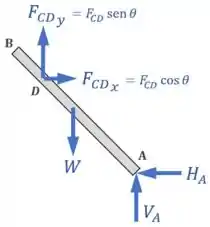
Em seguida, antes de podemos fazer o somatório de momentos , precisamos encontrar os braços das forças , e em relação ao ponto .
Então, vamos fazer uma pausa para olhar para os ângulos do exercício e encontrar os braços das forças!
O peso atua no meio da barra rígida de comprimento , mas a barra está com uma inclinação de , então temos que o braço do peso vai ser igual à , como mostra a figura:
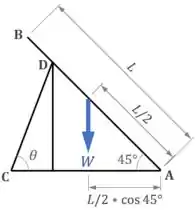
Já o braço da força vai ser igual à , como mostra a figura abaixo:
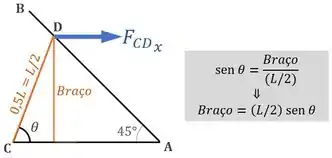
Por fim, o braço da força vai ser igual ao braço da força :
Passo 3
Agora que entendemos como são os braços das forças em relação ao ponto , podemos finalmente realizar o somatório de momentos:
As forças e vão realizar um momento no sentido anti-horário (), enquanto que a força vai realizar um momento no sentido horário ().
Dessa forma, o somatório de momentos fica assim:
Substituindo os valores encontrados para os braços, temos que:
Dividindo tudo por , isso fica assim:
Passando a parte que está subtraindo para o outro lado e depois substituindo e , encontramos que:
E, finalmente, isolando , encontramos uma expressão que descreve essa força:
Passo 4
Pronto! Agora que temos uma expressão que descreve a força , podemos passar a resolver os itens do exercício.
Começando pelo item : Calcular o ângulo para o qual a força na escora é mínima.
Bom, a força é dada por:
Essa expressão vai ser mínima quando a expressão “” que está dividindo ela for máxima.
Agora, se a gente se lembrar lá de cálculo, vamos nos lembrar que os máximos e mínimos das funções ocorrem quando as suas derivadas são iguais à zero.
Então vamos aplicar essa condição da derivada igual a zero aqui e descobrir qual é o valor de que satisfaz ela:
Usando a regra do produto , isso fica assim:
Lembrando que derivada de seno é cosseno e que derivada de cosseno é menos seno, conseguimos calcular essas derivadas:
E fazendo as multiplicações e arrumando tudo, isso fica assim:
Agora, eu não vou mentir: fiquei chateado/perdido com esse exercício quando cheguei aqui.
A gente quer isolar para descobrir o valor de que satisfaz a condição da derivada igual à zero, mas nessa expressão acima, não tem nenhum jeito fácil de isolar .

Aí eu fui dormir....
No dia seguinte, quando acordei, percebi que aquela expressão acima me lembrava das fórmulas do seno e cosseno de :
E pois não é que quando você usa que e , você encontra que:
Daí que, usando isso, você pode pegar a expressão que tinhamos encontrado:
E reescrever ela assim:
Passando pro outro lado, temos que:
Dividindo tudo por , isso fica assim:
E enquanto que o primeiro ângulo a ter uma tangente igual a é o ângulo de , o primeiro ângulo a ter uma tangente igual a é o ângulo de , de tal forma que:
Sendo assim, encontramos o ângulo para o qual a força vai ser mínima!
Felizmente, à partir daqui, o exercício fica mais tranquilo. 😊
Passo 5
Item resolvido, seguimos para o item : Calcular a força mínima.
Pegando a expressão que tinhamos encontrado para a força , temos que:
Como acabamos de ver que é mínima quando , a força mínima vai ser:
A gente pode deixar esse resultado em função dos senos e cossenos assim.
Ou a gente pode usar uma calculadora para encontrar o que todos esses senos e cossenos vão dar.
Usando a calculadora, encontramos que:
Passo 6
No próximo item, o item , queremos calcular a área da seção transversal da escora, sendo a tensão admissível do material da mesma.
Então vamos nos lembrar...
Se um material tem uma tensão admissível , isso significa que a tensão no material tem que ser menor ou igual que essa tensão admissível:
E a tensão normal na nossa escora pode ser dada pela fórmula da tensão normal média:
Agora, nós vimos lá no primeiro passo, quando entedemos o que estava acontecendo no exercício, que a escora está submetida a uma força de compressão .
Então a intensidade da força interna normal na nossa escora vai ser igual à intensidade dessa força , que calculamos como .
Fazendo essa substituição, a expressão anterior fica assim:
Isolando a área , que é o que queremos encontrar, obtemos que:
Ou seja, a área mínima da seção transversal da escora vai ser:
E assim finalizamos o item .
Passo 7
Para o item , queremos calcular o encurtamento da escora.
Esse encurtamento também pode ser entendido como a variação de comprimento que a escora sofre quando é comprimida e que é dada pela fórmula:
Sabemos que a escora possui uma força interna normal , e um comprimento .
E podemos considerar que ela possui um módulo de elasticidade e uma área igual a área mínima que ele pode ter, que foi encontrada no último item.
Fazendo isso, temos que:
Cortando em cima e em baixo e arrumando essa equação, ela fica assim:
Ou seja, o encurtamento na escora é:
Passo 8
Finalmente (!), chegamos ao item : Calcular a energia de deformação acumulada na escoa.
Se considerarmos que o material da escora está se comportando de forma linear-elástica/de acordo com a Lei de Hooke, vamos ter que a energia de deformação na escora vai ser dada por:
Onde:
- é a tensão na escora. Se considerarmos que a escora possui a menor área de seção transversal possível, vai ser igual a ;
- é a deformação na escora, que pode ser calculada pela Lei de Hooke . Considerando uma tensão , vamos ter que ;
- E é o volume da escora.
Fazendo essas considerações, a energia de deformação fica assim:
Arrumando, isso dá:
E, assim, finalizamos o exercício!
Resposta
Exercício Resolvido #7
Elaboração própria
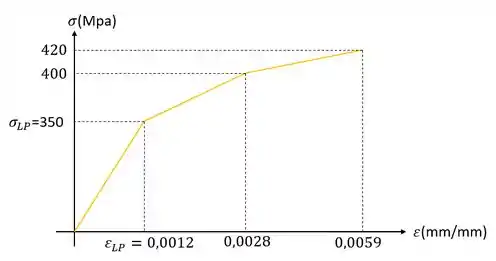
Com base no gráfico de tensão e deformação dado abaixo, determine o módulo de resiliência e de tenacidade desse material.
Passo 1
Para resolver esse exercício precisamos relembrar como determinar o modulo de resiliência e de tenacidade usando um gráfico de tensão por deformação. Vamos começar pelo modulo de resiliência.
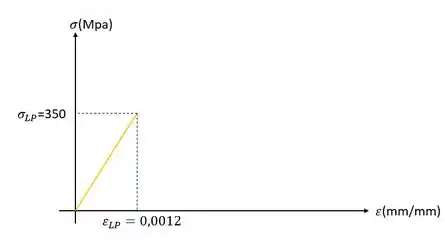
O modulo de resiliência é calculado pela fórmula
Em que são valores de tensão e deformação no limite de proporcionalidade. Se prestarmos atenção essa fórmula representa exatamente a área do primeiro triangulo que aparece na nossa figura, que representamos na imagem abaixo
Passo 2
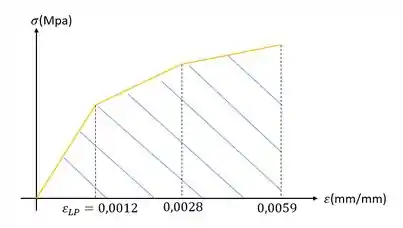
Já sabemos o que fazer com o modulo de resiliência, mas e o modulo de tenacidade?
O modulo de tenacidade é bem tranquilo, é só determinar a área abaixo do gráfico, como mostrado a seguir
Passo 3
Agora que já sabemos como calcular cada um desses valores, vamos determina-los.
Primeiro o modulo de resiliência.
Sabemos que
Como a fórmula é
Substituindo teremos que
Como queremos uma unidade de densidade de energia, multiplicaremos em cima e embaixo por metros, teremos então
Passo 4
Precisamos determinar também o modulo de tenacidade, e para isso precisamos calcular a área abaixo do nosso gráfico, vamos dividir então o nosso gráfico em três regiões de interesse.
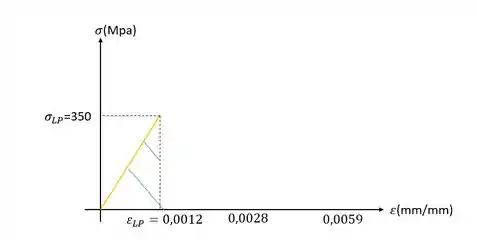
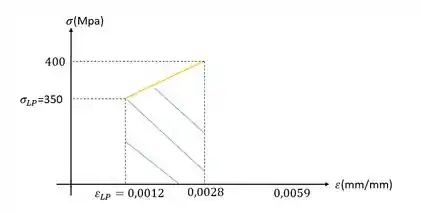
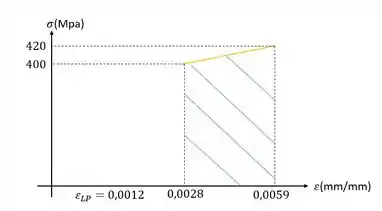
Agora basta calcularmos a soma dessas áreas para definirmos o modulo de tenacidade do nosso material.
Resposta
Exercício Resolvido #8
Elaboração própria
O pilar abaixo está submetido ao carregamento mostrado. Usando seus conhecimentos acerca de energia de deformação, determine o valor da energia de deformação dessa peça.
.
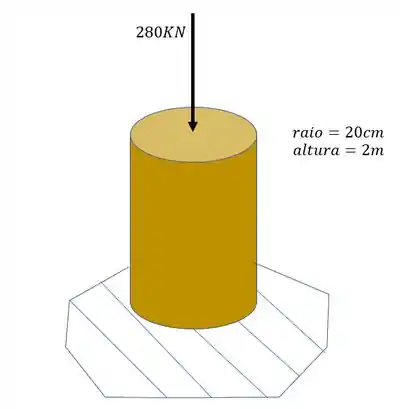
Passo 1
Esse exercício quer testar o nosso cuidado com unidades e aplicação de fórmula, então vamos tomar alguns cuidados nas nossas resoluções. Vamos primeiro determinar a fórmula que devemos usar.
Em que sabemos que podemos determinar cada termo dessa equação pelas fórmulas
Em que a área é
Sabemos também que podemos definir a deformação especifica pela lei de Hooke da seguinte maneira
E por fim sabemos que o volume nesse caso se trata do volume do cilindro que é dado por
Passo 2
Como já temos as nossas fórmulas, vamos substitui-las na equação principal.
Passo 3
Vamos agora substituir os valores que o enunciado nos dá e vamos determinar o valor da nossa energia
Calculando a energia teremos que