Método da seção de Richter Barras Secundarias
Produzido por Pablo RicardoTeoria
Introdução
Vimos na primeira parte como calculamos os normais pelo método da seção de Richter, agora iremos prosseguir com o cálculo, mas com a exceção de que agora calcularemos o normal inclinado, será exatamente esse o foco da segunda parte dessa aula. Bora lá então

- Passo 5: cálculo do normal
- Resumo
Como é uma força inclinada, vamos ter que decompor ele, mas não temos um ângulo, certo? Contudo temos os lados. Olhando a nossa seção com decomposto, teremos que.
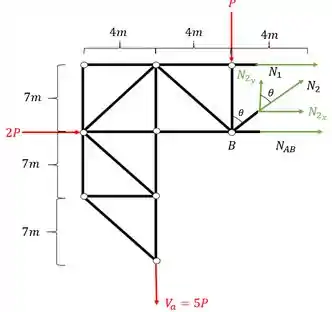
Decompondo a força teremos que
Se você olhar para o nosso exercício vai perceber que na horizontal temos a incógnita , então vamos fazer o equilíbrio na vertical que não tem nem e nem , fazendo o equilíbrio teremos
Logo
Mas quando vale o ângulo? Basta descobrimos o seu valor pela relação da nossa treliça em que
Então vamos fazer um resuminho do passo a passo
- Primeiro: calculamos as reações de apoio
- Segundo: definimos onde passar a seção e escolhemos qual dos lados da estrutura deveríamos usar para calcular
- Terceiro: equilibramos a nossa peça aplicando os normais correspondentes as barras que cortamos
- Quarto: calculamos o nosso normal através do somatório de momentos no nó que tiver mais incógnitas apontando para ele.
- Quinto: calculamos outra força normal através de outra equação de equilíbrio
Agora é só treinar com os exercícios que o 10 vem na certa!!!
Exercícios Resolvidos
Exercício Resolvido #1
Hibbeler – Exemplo 6.5
Determine a força nos elementos GE,GC e BC da treliça mostrada abaixo. Indique se os elementos estão sob tração ou compressão.
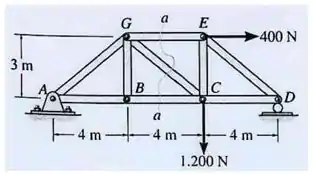
Passo 1
Bom, precisamos começar entendendo o enunciado,
De acordo com o enunciado, para esse exercício precisaremos calcular as reações nos elementos GE, GC e BC, a fim de entender quais elementos estão sobre tração e quais sobre compressão, mas dessa vez usando o método das seções. Bora lá?
Agora, precisamos entender quais são as reações nos apoios nessa treliça;
Temos dois apoios, um apoio de segundo gênero no ponto A e um apoio de primeiro gênero no ponto D.
No apoio do ponto A, existem uma reação Ax e uma reação Ay, visto que temos um apoio de segundo gênero.
Já no apoio do ponto D, existe apenas uma reação Dy, visto que temos um apoio de primeiro gênero.
O DCL do corpo ficará assim;
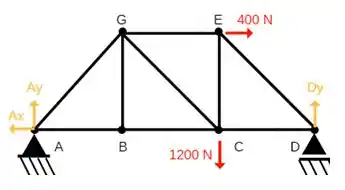
Passo 2
Agora, vamos escolher a melhor seção para dividir treliça!
Nesse exemplo cara, o enunciado facilitou um pouco a nossa vida, pois ele já deixou indicado que a melhor seção para cortarmos é a seção a-a.
Assim com o corte a treliça ficará dessa forma:
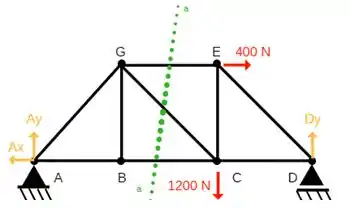
Mas porquê a melhor opção seria cortar a treliça nessa posição?
Essa posição foi escolhida, pois o corte nessa posição passa pelas três barras que precisamos determinar as reações. (Essa é uma dica muito importante, sempre corte as seções nos locais que seja possível pegar o maior número possível de barras que você deseja encontrar as reações)
Passo 3
Não me abandonou? Então continua aqui comigo...
Agora vamos determinar as reações externas em A e D, ou seja as reações dos apoios. Para isso precisamos aplicar as equações de equilíbrio, são elas:
Somatório das forças horizontais igual a zero:
Somatório dos momentos igual a zero:
Somatório das forças verticais igual a zero:
Passo 4
Vamos lá, já determinamos os valores de todas as reações externas, agora precisamos encontrar as reações nas barras desejadas! Para isso vamos isolar a seção da esquerda da treliça. (Super Dica: Tanto faz qual seção isolar, porém escolha sempre a que lhe parece ter contas mais fáceis, ou seja menos reações totais).
Vamos começar analisando a seção esquerda;
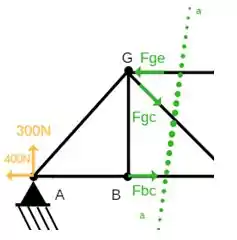
Somatório dos momentos em relação ao ponto G igual a zero: (Super Dica: escolha o ponto que tiver mais forças sendo aplicadas, para ser o referencial, para que elas sumam na conta)
(TRAÇÃO)
Da mesma forma, o somatório dos momentos em relação ao ponto C fornece uma solução direta para Fge;
(COMPRESSÃO)
Visto que Fbc e Fge não apresentam componentes verticais, o somatório das forças na direção vertical fornece diretamente Fgc, em outras palavras:
Somatório das forças verticais igual a zero:
(TRAÇÃO)
Resposta
(TRAÇÃO)
(COMPRESSÃO)
(TRAÇÃO)
Exercício Resolvido #2
Prova USP(Universidade de São Paulo )/PUC - Campinas - Professor José Luiz Arruda - Adaptado
Considere a treliça abaixo e determine as forças nas barras 4-6, 5-6 e 5-7. Para isso obrigatoriamente use o corte da seção definida por M-N. (Considere 0,8 t e 0,2 t como as forças realizadas pelos apoios)
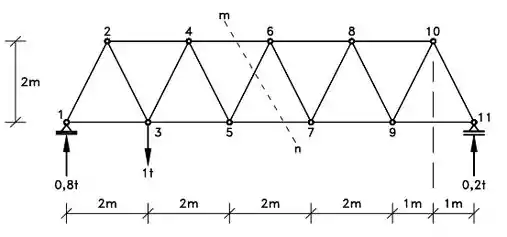
Passo 1
Faaala, nessa questão o professor, já especificou que precisaremos usar o corte M-N, para resolver a questão correto?
Significa então, que precisaremos utilizar o método das seções para poder determinar cada reação nas barras!
Nosso primeiro passo é escolher qual lado da treliça utilizar. Alguma ideia?
É isso mesmo que você está pensando... vamos utilizar o lado direito da treliça, pois o lado direito apresenta menos forças de reação do que o lado esquerdo, pelo falo de ter um apoio de primeiro gênero!
A princípio sempre é bom escolhermos o lado com menor número de reações.
Visto isso, teremos;
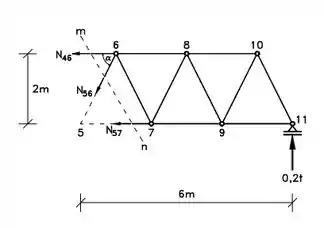
Passo 2
Agora com o lado da treliça escolhido, iremos aplicar as fórmulas de equilíbrio.
Importante (Vale lembrar que se a treliça toda está em equilíbrio, uma seção qualquer dela também está em equilíbrio)!Somatório dos momentos em relação ao Nó 5;
Somatório dos momentos em relação ao ponto 6;
Somatório das forças na vertical;
Agora temos um problema, como encontrar α?
Uma observação pontual pode resolver esse problema! Você reparou que podemos usar as propriedades de trigonometria e teremos que;
Retornando a conta da reação;
Resposta
As forças com sinal positivo são forças de tração, já as com sinal negativo são forças de compressão.
Exercício Resolvido #3
Elaboração Própria
Determinar as forças normais nas barras da treliça dada.
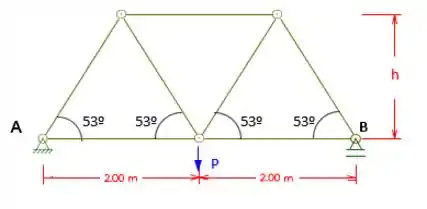
Passo 1
Vamos entender o enunciado... Bora lá?
De acordo com enunciado, precisamos encontrar todas as forças em todas as barras.
Porém antes, precisamos comentar duas coisas... a primeira é, você deve ter reparado que temos um h e um P que não estão identificados na questão correto?
Não se preocupe com isso, o h você vai ver comigo que vamos poder encontrar, porém o P é um valor incógnita, ou seja a resposta ficará em função de P. Você verá no final...
Agora vamos marcar as forças de reação na treliça em laranja, marca aí...
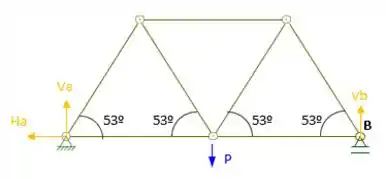
Não se esqueça, quando temos um apoio de primeiro gênero como o do ponto B, temos apenas esforço na vertical e quando temos um apoio de segundo gênero como o do ponto B, teremos esforço na horizontal e na vertical!Mais uma dica importante, você pode arbitrar a o sentido das forças como achar melhor ou até mais bonitinho, rs!
Pois caso você escolha uma direção e ela esteja errada, você vai encontrar no final o resultado com uma resposta negativa, e na mecânica resultados negativos caracterizam, que a direção é ao contrário do que arbitrou inicialmente!
Passo 2
Boa, agora que já marcamos as reações dos apoios, podemos descobrir outras informações sobre a treliça... Tô muito curioso para descobrir o valor de h, você não? Então vamor lá...
A altura h ela pode ser encontrada de diversas formas, porém a mais fácil e visual é através da aproximação a tangente, assim:
Cara, existe mais uma coisa que pode facilitar nossa vida, se você reparar devido à simetria da estrutura e do carregamento, podemos afirmar que:
Passo 3
Agora, para determinar a carga axial nas barras 1 e 2, aplica-se o corte AA e BB como na figura abaixo.
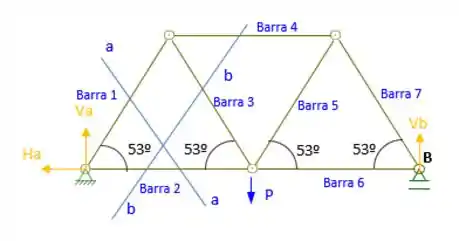
Para a parte esquerda do corte AA podemos obter:
Somatório das forças verticais igual a zero:
(Barra Comprimida)
Somatório das forças horizontais igual a zero:
(Barra Tracionada)
Para o corte BB podemos obter as forças nas barras 3 e 4:
Somatório dos momentos em relação ao ponto E:
(Barra Comprimida)
Somatório das forças verticais igual a zero:
(Barra Tracionada)
Super Dica: Como a treliça é simétrica, podemos concluir que:
Resposta
(Barra Comprimida) (Barra Tracionada) (Barra Tracionada) (Barra Comprimida) (Barra Tracionada) (Barra Tracionada) (Barra Comprimida)
Exercício Resolvido #4
Prova UFSC – Professor João Dirceu
Resolva a treliça abaixo pelo método das seções e determine as reações nas barras 1, 3 e 4.
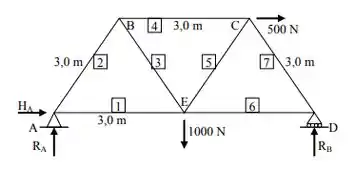
Passo 1
E aíii, beleza? Vamos ver mais essa questão juntos?
Bom como pudemos observar, o enunciado foi bem claro, deixou bem especificado que ele deseja utilizar o método das seções, para achar as forças de reação nas barras 1,3 e 4.
Para utilizar o método, primeiro precisamos verificar quais são os valores das reações dos apoios! Bora lá?

No nó A tempos um apoio de segundo gênero, dessa forma teremos uma força na horizontal e uma na vertical (Ha e Ra) e no nó D temos um apoio de primeiro gênero, com uma única reação na vertical (Rd).Dessa forma, podemos agora determinar o valor das reações.
Pera, pera, antes precisamos descobrir os ângulos entre as barras e a altura h , presente na treliça, não podemos esquecer disso!
Vamos observar a seção triangular composta pelas barras 1, 2 e 3.Como podemos perceber, ela tem uma seção triangular de lado igual a 3 metros, o que significa que teremos um triângulo equilátero, por consequência o ângulo α° = 60°, e a altura vai originar da fórmula da altura de um triângulo equilátero lá do ensino médio, que é:
Agoraaa sim, podemos voltar para o equilíbrio da treliça, então teremos;
Somatório dos momentos em relação ao ponto A:
Somatório das forças verticais iguais a zero
Somatório das forças horizontais iguais a zero:
Passo 2
Agora é a hora de separar as seções!
Eu pensei em dois possívei cortes, vou colocar eles aqui e aí você me ajuda a decidir qual é o melhor pode ser?
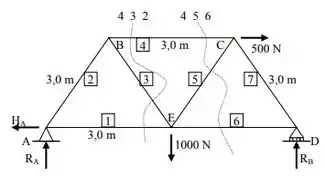
Não sei se faço o corte 4,3,2 ou o 4,5,6! Tá difícil a escolha....
Sabe porquê essa escolha se torna difícil?
Pois a princípio são cortes muito similiares, devido a treliça ter seções triangulares semelhantes, mas como nosso objetivo é descobrir as reações nas barras 1, 3 e 4, seria melhor se fizermos o corte 4,3,2 pois ele passa por mais elementos que desejamos encontrar.
Assim se fizermos um DCL desse corte teremos;
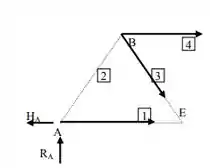
Agora vamos calcular o equilíbrio dos momenos em relação ao ponto B, vamos chamar de F1 a força realizada na barra 1;
Agora vamos calcular o equilíbrio dos momenos em relação ao ponto E, vamos chamar de F4 a força realizada na barra 4;
Agora vamos calcular o equilíbrio dos momenos em relação ao ponto A, vamos chamar de F3 a força realizada na barra 3;
Resposta
As forças com sinal positivo são forças de tração, já as com sinal negativo são forças de compressão.
Exercício Resolvido #5
PUC RIO – Professor Luciano – Questão 7
Determinar as forças normais nas barras da treliça dada
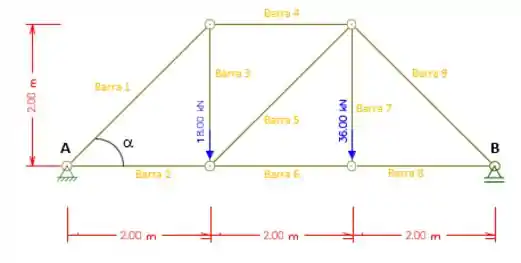
Passo 1
Cara, o enunciado diz para gente que precisamos determinar todas as reações de cada barra da treliça.
Se você percebeu , o único dado que não recebeu nenhum valor numérico foi o ângulo α.
Mas, como eu acho o ângulo α, já que ele não foi dado? Vem comigo que eu te mostro...
Se a gente observar bem, temos um triângulo retângulo isósceles, visto que a Barra 3 e a Barra 2 são perpendiculares entre si e ambas medem 2 m. Dessa forma conseguimos provar que o ângulo α = 45°. Ahh, mas eu não consegui ver o motivo de ser 45°, vamos lá fazer a conta então.
Passo 2
Agora podemos calcular as reações de apoio, porém para isso precisamo representar as forças na treliça, dessa forma iremos pintar de rosa as reações de apoio;
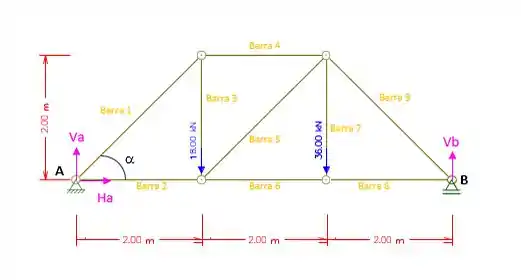
Somatório dos momentos em relação ao ponto A:
Somatório das forças horizontais iguais a zero:
Passo 3
Agora vamos fazer um corte AA representado pela figura abaixo, para determinar as formas nas barras 1 e 2.
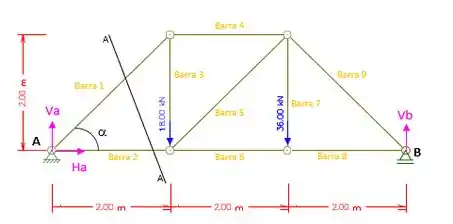
Somatório das forças verticais iguais a zero:
(Barra Comprimida)
Somatório das forças horizontais iguais a zero:
(Barra Tracionada)
Passo 4
Agora vamos fazer um corte BB representado pela figura abaixo, para determinar as formas nas barras 3 e 4.
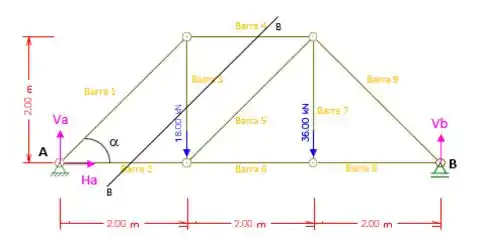
Somatório das forças verticais iguais a zero:
(Barra Tracionada)
Somatório dos Momentos em D igual a zero:
(Barra Comprimida)
Passo 5
Agora vamos fazer um corte CC representado pela figura abaixo, para determinar as formas nas barras 5 e 6.
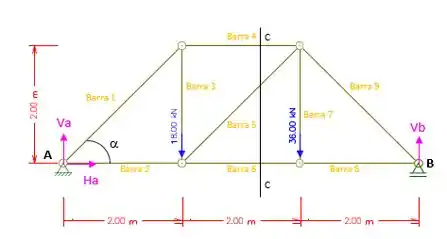
Somatório das forças verticais iguais a zero:
(Barra Comprimida)
Somatório dos Momentos em E igual a zero:
30 KN (Barra Tracionada)
Passo 6
Agora vamos fazer um corte DD representado pela figura abaixo, para determinar as formas nas barras 7 e 8. (Super Dica: As vezes fazer seções curvas pode facilitar muito as contas para isolar uma seção especial)
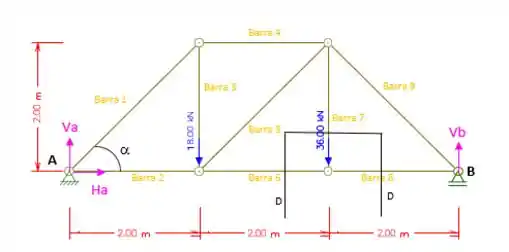
Somatório das forças verticais iguais a zero:
(Barra Tracionada)
Somatório das forças horizontais iguais a zero:
30 KN (Barra Tracionada)
Resposta
Agora vamos fazer um corte EE representado pela figura abaixo, para determinar a forma na barra 9.
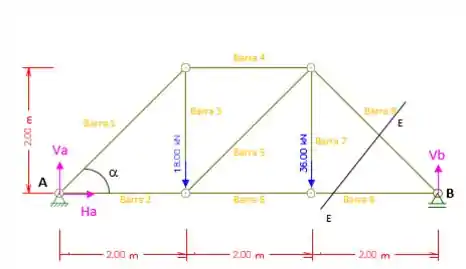
Somatório das forças verticais iguais a zero:
(Barra Comprimida)
Resposta
(Barra Comprimida)
(Barra Tracionada) (Barra Tracionada) (Barra Comprimida)
(Barra Comprimida)
30 KN (Barra Tracionada)
(Barra Tracionada) 30 KN (Barra Tracionada)
(Barra Comprimida)
Exercício Resolvido #6
Prova USP – Professor Valério
Determine os esforços normais nas barras CD, ID e IJ e comprove pelos dois lados da treliça o resultado encontrado. Justifique o motivo do resultado encontrado.
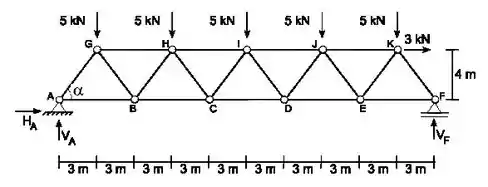
Passo 1
Fala pessoal, vamos ver mais essa questão sobre método das seções!
Vale ressaltar que dessa vez o enunciado quer que a gente comprove o nosso resultado pelos dois lados da treliça, ou seja vamo precisar realizar os cálculos tanto na seção esquerda quanto na seção direita do corte! Boraaaa?Primeiro precisamos verificar quais são os valores das reações dos apoios! Partiu???
Somatório dos momentos em relação ao ponto A:
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 2
Vamos escolher um corte que passe pelas três barras que desejamos determinar as reações.
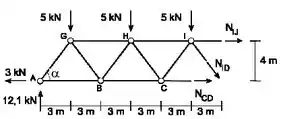
Agora que temos o corte definido vamos precisar analisar os dois lados, para determinar o que pede o enunciado.
Vamos começar pelo lado esquerdo da treliça;
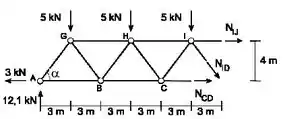
Podemos observar que temos um ângulo α°, e precisamos determinar ele certo?
Usando as regras da trigonometria do ensino médio vamos obter;
Assim;
Agora podemos fazer o somatório das forças verticais igual a zero;
Somatório dos momentos em relação ao ponto I igual a zero;
Somatório dos momentos em relação ao ponto D igual a zero;
Passo 3
Agora vamos refazer todos os cálculos só que tendo como referencial a seção direita da treliça;
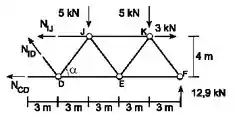
Agora podemos fazer o somatório das forças verticais igual a zero;
O valor de Nid, bateu com a resposta anterior encontrada.
Somatório dos momentos em relação ao ponto I igual a zero;
O valor de Ncd, bateu com a resposta anterior encontrada.
Estamos quase láaa! Desiste não...
Somatório dos momentos em relação ao ponto D igual a zero;
O valor de Fcd, bateu com a resposta anterior encontrada.
Resposta
As forças com sinal positivo são forças de tração, já as com sinal negativo são forças de compressão.
A resposta pode ser justifica, pelo fato de que toda vez que um corpo está em equilíbrio, é correto considerar que qualquer parte do mesmo também estará em equilíbrio, ou seja , independente de qual parte da treliça estudarmos, ambas vão estar em equilíbrio e manter suas respectivas reações de compressão ou tração. Por isso independe o caminho ou o lado que iremos escolher para achar os resultados.
Exercício Resolvido #7
Prova USP - Adaptado
Determine atráves do método das seções, as forças normais nas barras 3, 5 e 6.
Passo 1
Como o nosso enunciado já diz, precisaremos determinas as forças nas barras 3, 5 e 6! Certo?Para isso vamos precisar pensar quais seções vamos precisar separar para podermos calcular as forças nas barrras acima descritas?Para isso temos que pensar na forma que a treliça ocupa! Ela é completamente simétrica entã seria vantajoso cortar a treliça em maior partes iguais para justificar simetrias! Pescou?
Assim, nossa primeira seção vai ser limitada por um corte que passa pelas barras 5,3,4 e 8. Como na figura abaixo!
Assim, iremos analisar então a parte superior ao corte e poderemos calcular as reações;
Somatório dos momentos em relação ao ponto D:
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 2
Agora é a hora de separar novas seções que ainda possam nos ajudar!Como só achamos o falor de F5, ainda precisamos encontrar F3 e F6. Então nosso próximo passo vai ser cortar as barras em 5, 6, 7 e 8.
Assim, iremos analisar então a parte superior ao corte e poderemos calcular as reações;Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 3
Por último temos que encontrar ainda a força em 3, para isso vamos cortar a treliça passando pelas barras 2, 3 e 5.
Assim, iremos analisar o último corte!
Somatório dos momentos para um lado superiror da seção!
Resposta
Exercício Resolvido #8
Prova USP – Professor Valério
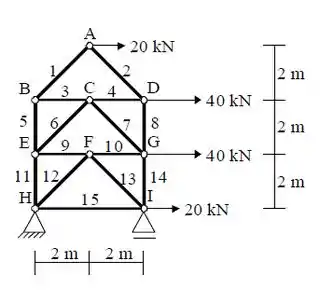
Empregando necessariamente o processo das seções, determinar as forças normais nas barras 9, 10, 11 e 12 da treliça da figura, indicando claramente se essas forças são de tração ou de compressão. No final, escreva essas normais obtidas no espaço indicado.
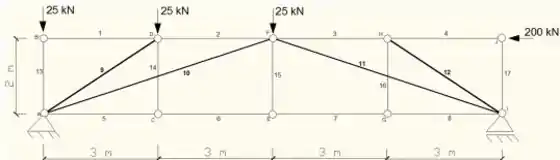
Passo 1
Fala pessoal, vamos ver mais essa questão sobre método das seções!Primeiro precisamos verificar quais são os valores das reações dos apoios! Bora lá?No nó A tempos um apoio de segundo gênero, dessa forma teremos uma força na horizontal e uma na vertical (Ax e Ay) e no nó I temos um apoio de um gênero, com uma única reação na vertical (Iy).Dessa forma, podemos agora determinar o valor das reações.
Somatório dos momentos em relação ao ponto A:
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 2
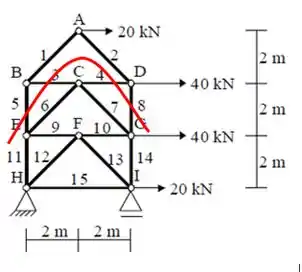
Agora é a hora de separar novas seções que ainda possam nos ajudar!Como ainda precisamos encontrar N10, então nosso próximo passo vai ser realizar um corte passando nas barras em 2,10 e 6. Para facilitar nossas contas.
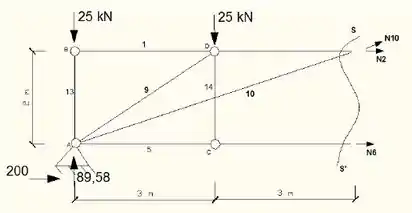
Assim, iremos analisar então a parte superior ao corte e poderemos calcular as reações;Somatório das forças verticais iguais a zero: (Super Dica, para encontrar o ângulo(Ѳ) que é o ângulo de encontro com a barra 10 e a barra 5 precisamos realizar trigonometria para triângulos retângulos
(Super Dica, para encontrar o ângulo(Ѳ), que é o ângulo de encontro entre as barras 10 e 5 precisamos realizar trigonometria para triângulos retângulo)
Logo,
87
Passo 3
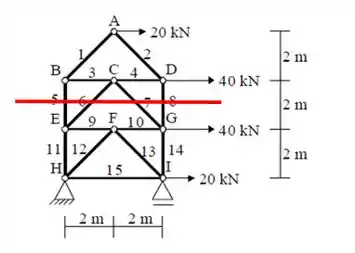
Agora vamos aproximando o corte do nó B, para facilitar na identificação das forças, ajudando principalmente a encontrar o valor de força exercida na barra 9. Bora lá?
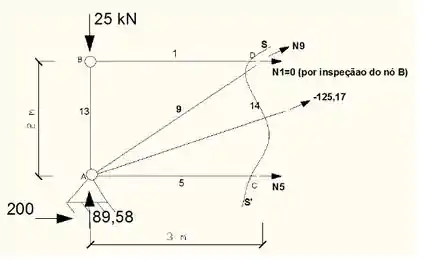
Somatório dos momentos em relação ao ponto C;
(Super Dica, para encontrar o ângulo(Ѳ), que é o ângulo de encontro entre as barras 10 e 5 precisamos realizar trigonometria para triângulos retângulo)
Logo,
Passo 4
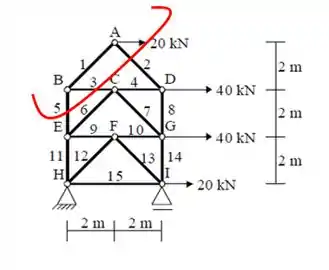
Agora vamos olhar para o lado direito da treliça, para encontrar o valor de força exercida na barra 11. Vamos? Não desanima não!
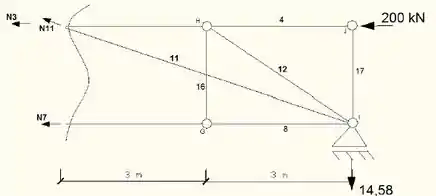
Somatório das forças verticais igual a zero;
Passo 5
Agora vamos aproximar mais o corte para direita, para encontrar o valor de força exercida na barra 12. Partiu?
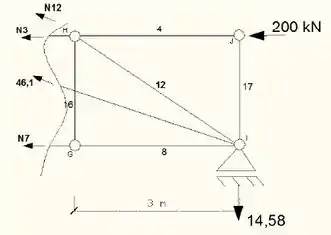
Somatório das forças verticais igual a zero;
Resposta
As forças com sinal positivo são forças de tração, já as com sinal negativo são forças de compressão.