Método do Equilíbrio de Nós Secundários
Produzido por Pablo RicardoTeoria
Introdução
Na parte anterior, aprendemos a fazer os cálculos do equilíbrio do nó A. agora nessa aula, aprenderemos a escolher os próximos nós de cálculo, assim como aprenderemos a calcula-los, vamos nessa então!!

Equilíbrio do nó B
Vimos que sempre a melhor opção de escolha são dos nós que possuem 2 barras chegando ou saindo deles, nesse caso os melhores nós para escolhermos são o nó A e B
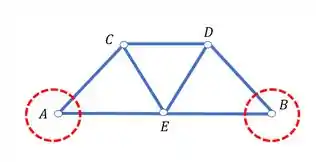
Ou seja, o processo de cálculo para o nó B é idêntico ao do nó A, maaaas, tome muito cuidado, apesar da treliça ser simétrica, as cargas não são, logo, o valor dos normais também não são iguais por simetria, no caso para o nó B teremos
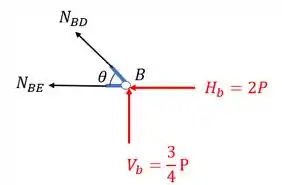
Fazendo a decomposição
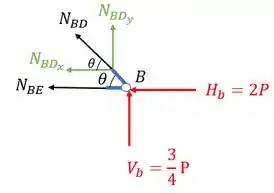
Sabemos que
E o ângulo continua sendo
Fazendo o equilíbrio teremos que
- O nó C tem 3 barras, mas uma delas é conhecida, ou seja, só tem duas barras desconhecidas, como os nós A e B, ou seja, resolvemos da mesma maneira de sempre.
- O nó D possui 3 barras, mas olha só, tem uma conhecida, logo, só tem 2 desconhecidas, então também dá pra resolver.
- Por fim o nó E tem 4 barras, agora não dá, certo? Errado, dá sim, são 4 barras, com 2 conhecidas, logo, sobram duas desconhecidas também, o que torna todos os nós possíveis de serem calculados.
Mas já determinamos cada um desses termos, substituindo
Como já temos os valores de basta que façamos a substituição
Escolha e equilíbrio dos próximos nós
Beleza, já solucionamos os nós com duas barras, e agora?

Agora é simples, marca na treliça todas as barras que você já calculou e os nós que faltam.
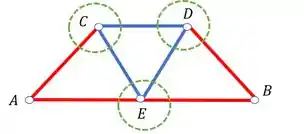
Perceba que
Vamos então ver o equilíbrio dos nós C e D.
Equilíbrio do nó C
Já sabemos que temos que cortar nossas barras, então vamos lá
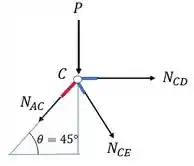
Não esquecer o carregamento P, as vezes nos distraímos na prova e acabamos esquecendo que no equilíbrio de nós o carregamento entra
Aqui precisamos adaptar o ângulo que estávamos usando antes, para podermos decompor o vetor , dessa forma teremos que
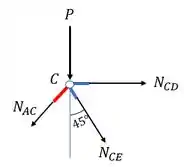
Decompondo teremos
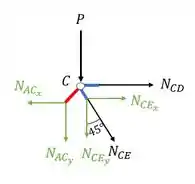
Aqui vale relembrar que a decomposição do vetor já foi feita antes, então aqui apenas usaremos o que já foi calculado. Decompondo teremos
Fazendo o equilíbrio teremos que
Mas já determinamos cada um desses termos, substituindo
Sabemos que
Substituindo
Equilíbrio do nó D
Agora vamos direto para o equilíbrio do nó, pois veja que o processo é exatamente igual tomando os devidos cuidados para cada um dos nós.
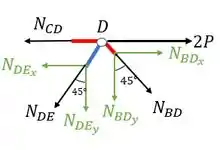
Fazendo o equilíbrio teremos que
Mas já determinamos cada um desses termos, substituindo
Como já determinamos o valor do normal da última barra não é necessário calcular o equilíbrio em x, logo, os normais na nossa barra são
Agora vamos exercitar pra ficarmos craque nesses cálculos!!!
Escolha e equilíbrio dos próximos nós
Equilíbrio do nó C
Equilíbrio do nó D
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
A treliça abaixo pode ser considerada uma treliça simples. Usando seus conhecimentos sobre treliças determine
- Quais os 2 primeiros nós que devemos resolver
- Qual a ordem de nós a serem resolvidos
- O valor do normal em todas as barras da treliça
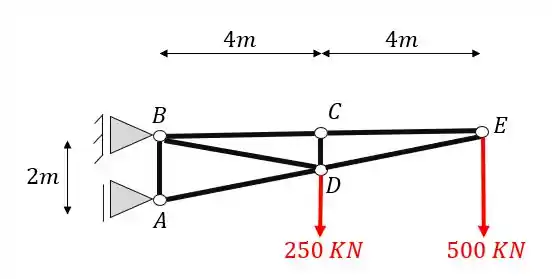
Passo 1
Para resolver os problemas sobre treliças precisamos seguir uma sequência de passos que facilita a resolução, em que temos que respeitar o seguinte
- Primeiro devemos calcular as reações de apoios da nossa treliça, que será calculada levando em consideração dois fatores
- A segunda coisa que devemos analisar nesse exercício é o melhor nó, e para isso temos que lembrar que no equilíbrio de nós sempre iremos usar as seguintes equações
- A terceira coisa que devemos ver é que sempre que resolvemos uma barra, tiramos uma incógnita do nosso problema, ou seja, se tivermos nós que compartilhem a mesma barra, pro nó ainda a ser resolvido, a barra compartilhada com ele o ajudará a calcular as desconhecidas, sempre, é claro, respeitando a regra de duas barras desconhecidas por nó, como vimos na teoria.
As reações

E as equações de equilíbrio
Ou seja, se temos duas equações, só podemos ter duas incógnitas para resolver o nosso nó.
Como cada barra representa uma incógnita, e que pelo passo anterior já teremos calculado as reações de apoio, sabemos que as únicas incógnitas serão as barras, e lembre-se, se cada barra é uma incógnita, e eu só posso ter duas incógnitas por nó, os melhores nós para iniciarmos serão aqueles que tem duas barras.
Se seguirmos esse último passo ao pé da letra, conseguiremos resolver tranquilamente todas as barras de uma treliça.
Agora que já conhecemos os três passos da nossa solução, vamos aplicar eles ao nosso problema.
Passo 2
A primeira coisa que devemos fazer como vimos no nosso passo a passo é definir as reações de apoio. Para isso devemos primeiro determinar os vetores reações de apoio e lembrar que sempre consideramos a nossa treliça como um elemento solido e único que usamos para determinar essas reações, com isso teremos que o nosso diagrama de corpo livre será
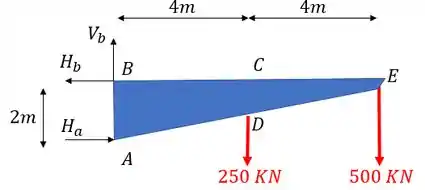
Definido os vetores reações de apoio já podemos usar as fórmulas de equilíbrio
Substituindo
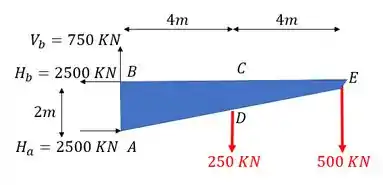
Assim já cumprimos a primeira parte do nosso passo a passo.
Passo 3
Agora que já cumprimos a primeira parte, precisamos fazer a segunda parte, que consiste em definir os melhores nós a serem calculados, e o valor do normal nas barras desses nós.
Como vimos anteriormente, os melhores nós para iniciarmos são aqueles que possuem somente duas barras, já que como vimos, cada nó só pode ter duas barras desconhecidas.
Com isso a nossa barra tem que os melhores nós que ela possui para iniciarmos os cálculos são
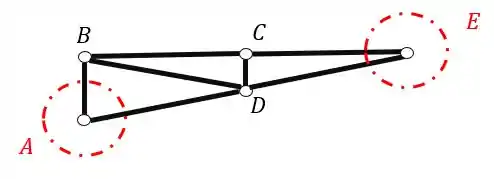
Pois são os únicos nós que possuem somente duas barras, logo, são os melhores para iniciarmos.
Passo 4
Agora precisamos fazer o equilíbrio dos nós, vamos começar pelo nó A.
Sabemos que a primeira coisa que devemos fazer é isolar o nó como vemos abaixo

A segunda coisa que devemos fazer é colocar os normais saindo das barras cortadas
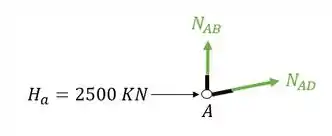
A terceira coisa que devemos fazer é definir o seno e o cosseno do ângulo entre as barras, pra isso usaremos as medidas dadas na nossa treliça
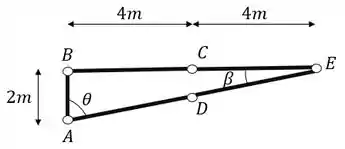
Sabemos que podemos calcular o nosso ângulo pela tangente, dessa forma teremos
Qual ângulo tem tangente igual a 4?
Agora já conseguimos decompor os nossos normais, já que já temos os ângulos, vamos calcula-los então.
Passo 5
Vamos lá então, decompondo os nossos normais teremos que
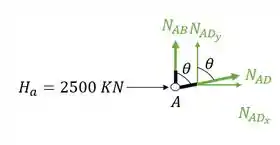
Fazendo a decomposição teremos que
Substituindo e fazendo o equilíbrio teremos que
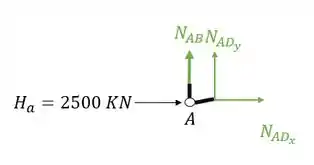
Sabemos que , substituindo teremos que
Logo
Substituindo no segundo sistema teremos
Então já calculamos os normais das barras do nó A.
Passo 6
Vamos agora calcular os normais do segundo nó, o nó E, sabemos que a primeira coisa que devemos fazer é isolar o nó como vemos abaixo
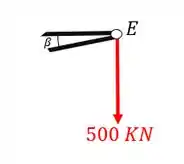
A segunda coisa que devemos fazer é colocar os normais saindo das barras cortadas
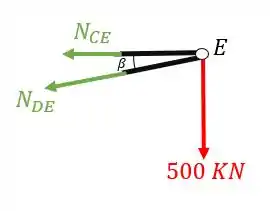
Agora já conseguimos decompor os nossos normais, já que já temos os ângulos, vamos calcula-los então.
Passo 7
Vamos lá então, decompondo os nossos normais teremos que
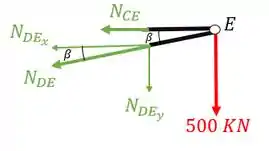
Fazendo a decomposição teremos que
Substituindo e fazendo o equilíbrio teremos que
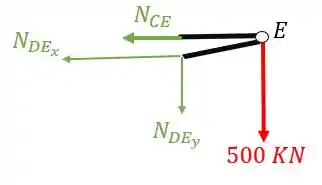
Sabemos que , substituindo teremos que
Logo
Substituindo no segundo sistema teremos
Então já calculamos os normais das barras do nó E.
Passo 8
Marcando de vermelho na nossa treliça as barras calculadas, teremos que
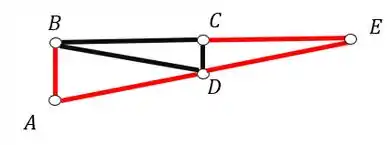
Perceba que o próximo nó a ser escolhido, só pode no máximo ter 2 barras desconhecidas, caso contrário, não conseguiremos calcular essas barras, porém, se prestarmos bem a atenção, veremos que todos os nós que faltam(B, C e D) possuem apenas duas barras desconhecidas (barras pretas), dessa forma podemos escolher qualquer um desses nós que faltam para fazermos o equilíbrio.
Como o nó C é composto apenas de barras perpendiculares, irei escolher esse nó para prosseguirmos o cálculo.
Passo 9
Sabemos que a primeira coisa que devemos fazer é isolar o nó como vemos abaixo
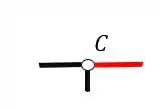
A segunda coisa que devemos fazer é colocar os normais saindo das barras cortadas
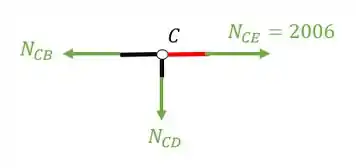
Substituindo e fazendo o equilíbrio teremos que
Então já calculamos os normais das barras do nó C.
Passo 10
Agora falta apenas a barra BD, vamos fazer o equilíbrio do nó B
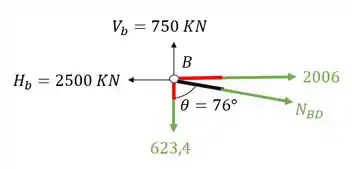
Decompondo os nossos normais teremos que
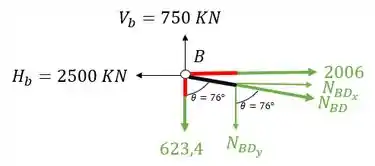
Fazendo a decomposição teremos que
Substituindo e fazendo o equilíbrio teremos que
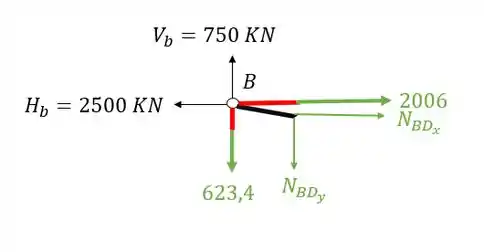
Substituindo teremos que
Logo
Com isso calculamos o normal de todas as barras que precisávamos, resolvendo assim a questão.
Resposta
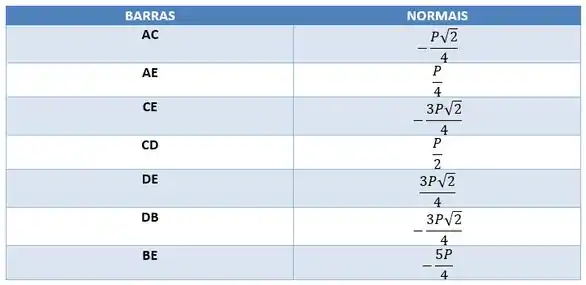
Os Normais são
Exercício Resolvido #2
PUC RIO – Professor Luciano – Questão 4
Determine as forças normais nas barras na treliça dada:
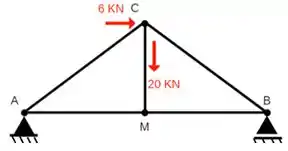
Dados : AB = 4 m, M é ponto Médio, MC = 1,5 m e Ângulo(cab) = Ângulo(abc) = α °
Passo 1
Vamos entender o enunciado...
De acordo com enunciado, precisamos encontrar todas as forças em todas as barras.
Porém para isso, precisamos descobrir o valor do ângulo α°, pois precisaremos dele para fazer projeções das forças normais nas barras AC e BC.

Para isso iremos precisar lembrar de nossas fórmulas de ensino médio... mais conhecidos como bons tempos!
Usaremos relações métricas no triângulo retângulo ACM:
Passo 2
Agora precisamos determinar, quais são as reações existentes na treliça! Vaaaamos?
Começamos, desenhando em rosa todas as reações existentes que são realizadas pelos apoios.
São elas:
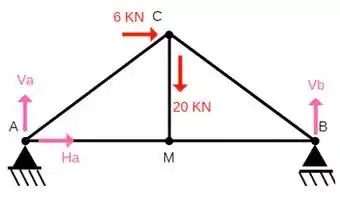
Super Dica: Precisamos sempre lembrar que quando temos um apoio de primeiro gênero como o do ponto B, temos apenas esforço na vertical, e quando temos um apoio de segundo gênero como o do ponto A, teremos esforço na horizontal e outro na vertical!Vale lembrar também que, você pode arbitrar a o sentido das forças como você preferir, caso você escolha uma direção e ela esteja errada, você vai encontrar no final o resultado com uma resposta negativa!
Na mecânica resultados negativos caracterizam, que a direção é ao contrário do que arbitrou inicialmente!
Agora, podemos verificar a Isostática da treliça, segundo a fórmula:
Onde n = 4 pois temos os nós A,B ,C e M;
b = 5, pois temos cinco barras;
v = 3, pois temos três reações nos apoios.
Assim,
Passo 3
Agora que provamos que a treliça é isostática, é a hora calcular as reações de apoio.
Vamos usar as condições para a treliça estar em equilíbrio, lembrando são elas;
Somatório dos momentos em relação ao ponto A igual a zero! (Aqui nós iremos arbitrar como ;positivo os momentos que seguirem no sentindo horário em relação ao relógio). Assim.
-
Somatório das forças verticais igual a zero!
Somatório das forças Horizontais igual a zero!
Passo 4
Agora iremos Anlisar cada Nó da treliça.
Vamos começar analisando o nó A;
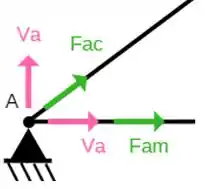
Somatório das forças verticais igual a zero!
Somatório das forças Horizontais igual a zero!
Agora escolhemos o ponto B por ter menos reações:
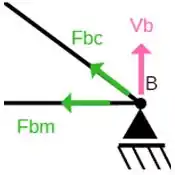
Somatório das forças Verticais igual a zero!
Somatório das forças Horizontais igual a zero!
Agora podemos observar que
Resposta
Exercício Resolvido #3
UFF – Professora Salete - Número 5
Calcule as reações de apoio e as forças normais nas barras através do Método dos Nós. Dado: Ângulo(cae) = ângulo(cde) = 26,57°
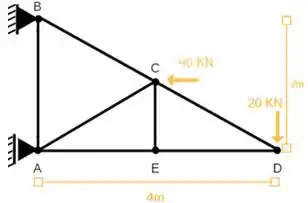
Passo 1
Nosso primeiro passo vai ser entender o enunciado, de acordo com enunciado, precisamos encontrar todas as forças normais em todas as barras. Para isso agora precisamos determinar, quais são as reações existentes na treliça! Vamos lá?
Começamos, desenhando em vermelho todas as reações existentes que são realizadas pelos apoios. São elas:
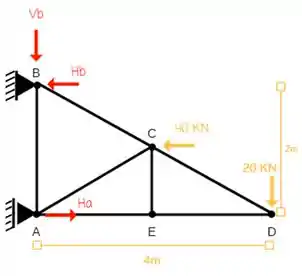
Não se esqueça, quando temos um apoio de primeiro gênero como o do ponto A, temos apenas esforço na vertical e quando temos um apoio de segundo gênero como o do ponto B, teremos esforço na horizontal e na vertical!Mais uma dica importante, você pode arbitrar a o sentido das forças como achar melhor ou até mais bonitinho, rs!
Pois caso você escolha uma direção e ela esteja errada, você vai encontrar no final o resultado com uma resposta negativa, e na mecânica resultados negativos caracterizam, que a direção é ao contrário do que arbitrou inicialmente!
Agora, podemos verificar a Isostática da treliça, segundo a fórmula:
Onde n = 5 pois temos os nós A,B,C,D e E;
b = 7, pois temos sete barras;
v = 3 , pois temos três reações nos apoios.
Assim,
Passo 2
Agora é a hora calcular as reações de apoio.
Vamos usar as condições para a treliça estar em equilíbrio, lembrando são elas;
Somatório dos momentos em relação a um ponto igual a zero!
Somatório das forças verticais igual a zero!
Somatório das forças Horizontais igual a zero!
Mais uma dica importante,
Passo 3
Agora iremos Anlisar cada Nó da treliça.
Vamos começar analisando o nó B;
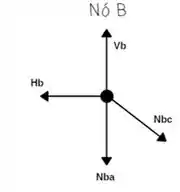
Somatório das forças Horizontais igual a zero!
Somatório das forças verticais igual a zero!
;
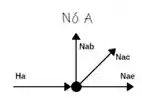
Somatório das forças verticais igual a zero!
Somatório das forças Horizontais igual a zero!
Agora vamos analisar o nó E;
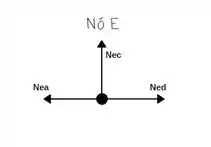
Somatório das forças Horizontais igual a zero!
Somatório das forças verticais igual a zero!
Agora vamos analisar o nó C;
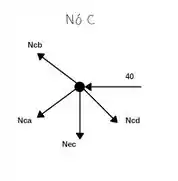
Somatório das forças Horizontais igual a zero!
(Dica importante, quando começarmos a chegar em equações que destinem como igualdade 0 = 0, significa que estamos próximos de já conhecer todas as reações existentes na treliça)
Somatório das forças verticais igual a zero!
Agora vamos analisar o nó D;
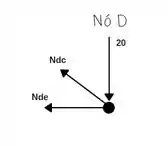
Somatório das forças Horizontais igual a zero!
Somatório das forças verticais igual a zero!
Resposta
Exercício Resolvido #4
Prova USP – Professor Valério
Para a treliça a seguir, determinar seus esforços em cada barra. Indique as barras que estão tracionadas ou comprimidas.
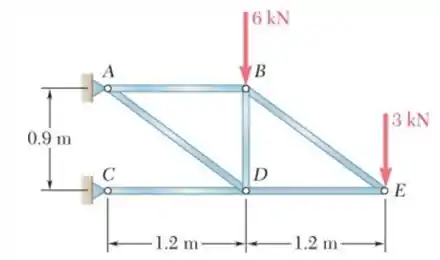
Passo 1
Nosso primeiro passo é entender o enunciado e pensar na melhor maneira de solucionar a questão!!
Como o nosso enunciado já diz, precisaremos determinar os esforços em cada barra! Certo?Para isso vamos precisar pensar qual seria o melhor método para resolver a questão... Pensou nisso também? É isso mesmo, iremos usar o método dos nós, isolar os nós para poder descobrir cada uma das forças, uma dica muito irada é que quase sempre que precisarmos encontrar todas as reações em cada barra, precisaremos usar o método dos nós.
Então bora lá usar o método dos nós...
Uma boa observação, é você perceber que a princípio as reações do apoio não vão influenciar nas contas para encontrar as reações das barras! Por isso iremos começar isolando o ponto oposto aos apoios!
Passo 2
Vamos isolar então o ponto E da treliça;
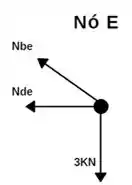
Um detalhe importante, como podemos ver a força Nbe não está alinhada nos eixos, por isso vamos precisar decompor ela!Para isso precisamos saber o seno e o cosseno do ângulo entre Nbe e Nde.
Vamos chamar esse ângulo de Ѳ, assim podemos afirmar que atráves das medidas das barras;Assim,
Temos , agora partiu aplicar as fórmula de equilíbrio???
Vamos lá...
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 3
Próximo nó que podemos isolar é o nó B;
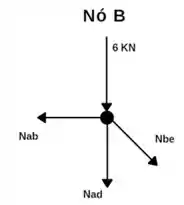
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 4
Próximo nó que podemos isolar é o nó D;
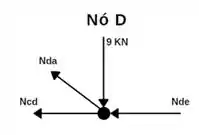
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Resposta
Todas as forças positivas são forças de tração e todas as forças negativas são forças de compressão.
Exercício Resolvido #5
Prova UFSC – Questão 3
a) Determine as forças normais nas barras da treliça da figura abaixo.
b) Sabendo que as barras desta treliça se rompem para forças de compressão de 100 KN e para forças de tração de 200 KN, determinar o valor de P que levaria essa treliça a ruptura.
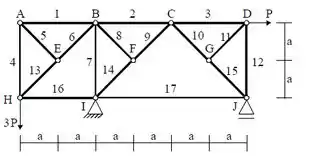
Passo 1
Esse exercício é separado em duas partes, então vamos começar resolvendo a letra (a) e depois vamos para (b), de forma a ficar mais claro, como resolver!
Bom na letra (a), precisamos usar o método dos nós para poder encontrar todas as reações presentes nas barras da treliça.
Vamos começar marcando as reações dos apoios, são elas:
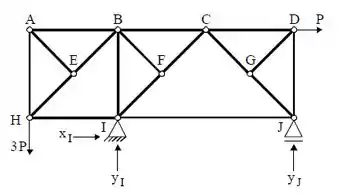
Agora vamos utilizar o equilíbrio da treliça;
Somatório dos momentos em relação ao ponto I:
Somatório das forças horizontais igual a zero:
Somatório das forças verticais igual a zero:
Passo 2
Para esse tipo de exercício, podemos utilizar um macete para facilitar nossas contas, como pudemos perceber as treliças estão meio que todas com a mesma inclinação, podemos tentar rotacionar nosso eixo de referencial para facilitar as contas!
Seguindo essa linha de pensamento, podemos começar pelo Nó E, que é um nó central ao quadrado ABIH, e aí poderemos observar que:
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Seguindo essa mesma linha de raciocínio, teremos no Nó F;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Seguindo essa mesma linha de raciocínio, teremos no Nó G;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Seguindo essa mesma linha de raciocínio, teremos no Nó A;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Seguindo essa mesma linha de raciocínio, teremos no Nó D;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 3
Agora, iremos observar nós um pouco mais complexos, como o Nó H;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Agora o nó B;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Agora o nó I;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Agora o nó J;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 4
Resolvendo a letra (b)
Precisamos entender o seguinte, a treliça se rompe em duas condições:
A primeira, é se as barras sofrerem uma compressão de no máximo 100 KN e a segunda se tração for de no máximo 200 KN.
Então precisamos pensar no seguinte!
De todas as barras que sofrem compressão (+), qual é a maior? Concorda comigo que é são as barras 7 ou 16. Assim,
De todas as barras que sofrem compressão (+), qual é a maior? Concorda comigo que é são as barras 6 ou 13. Assim,
32P=100P=47,14 K
Dessa forma, podemos concluir que a treliça se rompe para P = 33,33 K
Resposta
(a)
N1 = 0 KN
N2 = 3P KN
N3 = P KN
N4 = 0 KN
N5 = 0 KNN6 = 3P KN
N7 = -3P KN
N8 = 0 KN
N9 = -P KNN10 = P KNN11 = 0 KNN12 = 0 KNN13 = 3P KNN14 = -P KNN15 = P KNN16 = -3P KNN17 = -P KN
(b) A barra se rompe para P = 33,33 KN