Método do Equilíbrio de Nós
Produzido por Pablo RicardoTeoria
Nesse tópico vamos ver o seguinte:
- Determinação das reações de apoio de uma treliça
- Cálculo dos esforços internos de cada barra a partir do equilíbrio dos nós
- Determinação se o normal é de compressão ou de tração
- Como escolher o nó correto para inicia e os nós posteriores ao primeiro
- Para fazermos o equilíbrio em um nó teremos a ajuda de duas equações, sendo elas
- Como só temos duas equações para nos ajudar, quando formos escolher o nó teremos que escolher um número de incógnitas compatíveis, ou seja, se só temos duas equações, em cada nó só poderemos ter duas incógnitas. Como já determinamos as reações de apoio, as únicas incógnitas são as barras. Agora vem o pulo do gato.
- Se estiver saindo da barra e for positivo o resultado, então o nosso normal traciona a barra.
- Se estiver saindo da barra e for negativo o resultado, então o nosso normal está comprimindo a barra.
Com isso conseguimos resolver qualquer problema de treliças pelo método do equilíbrio de nós, então vamos lá?

Situação
Para entendermos o passo a passo da solução de uma treliça precisamos antes de tudo de uma situação que nos permita fazer esse cálculo, com isso imagine que o enunciado da prova peça para você determinar o valor dos esforços normais em todos as barras da treliça dada abaixo:
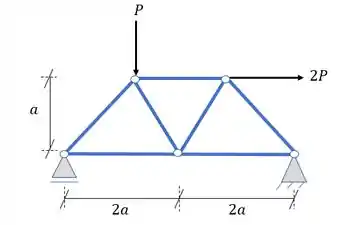
Como seu professor é muito bonzinho ele não coloca nenhum número, só letra, e agora, como fugir dessa maldição?

Ai que vamos aprender a mágica para resolver esse problema.
Reações dos apoios
Para determinar as reações de apoio em uma treliça basta que pensemos nela como um copo rígido inteiro, ou seja, ao invés de olharmos para ela como varias barras, olhamos para ela como um grande sólido, como mostra a figura abaixo
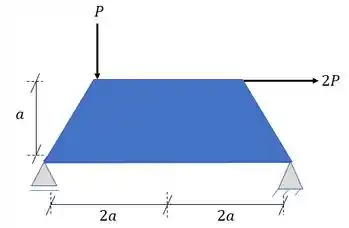
Sabemos que o próximo passo é trocar os apoios pelas reações de apoio, dessa forma teremos que
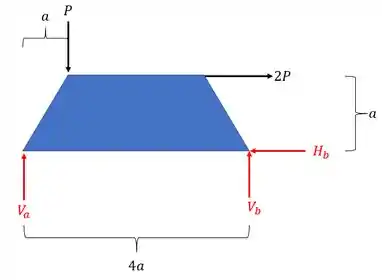
Para acharmos as reações basta que façamos o uso das equações de equilíbrio
Substituindo
Escolha dos nós
Agora que já determinamos as reações dos apoios temos que escolher o melhor nó para começarmos. Para isso temos que pensar da seguinte forma:
Não temos o auxilio da equação do momento pois estamos avaliando um nó por vez, ou seja, as forças sempre estarão concentradas no nó, então sempre que formos calcular o momento no nó ele dará zero, o que não nos ajuda em absolutamente nada.

O melhor nó a ser escolhido em primeiro lugar é aquele que só tiver duas barras nele, ou seja, no nosso exemplo, os únicos nós com apenas duas barras são os nós dos apoios, logo, são eles as melhores opções para começarmos. Vamos nomear os nós para facilitar o processo.
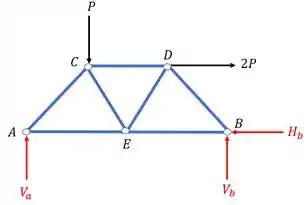
Equilíbrio do nó A
Para fazermos o equilíbrio do nó, devemos cortar as barras que saem dele e trocarmos elas por esforços. Como já sabemos, os esforços que agem nas barras são os esforços normais, por conveniência, sempre fazemos eles saindo das barras, porque fazemos assim? Só pelo seguinte
Vamos ver isso na pratica.
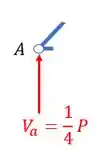
Como podemos ver, quando partimos as barras do ponto A temos a configuração mostrada acima, porém trocamos as barras por esforços, logo teremos.
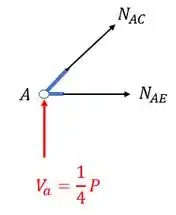
Perceba que o nome que demos aos normais são os nomes das barras, assim fica mais fácil identificar quem é quem. Agora vem a parte complicada das treliças. Sempre teremos barras inclinadas, e essas barras terão forças inclinadas, e para equilibra-las temos que decompor essas forças, pra isso precisamos dos ângulos dessas barras, então vamos determinar os ângulos.
Determinação do ângulo
Sabemos que olhando as dimensões da nossa seção teremos
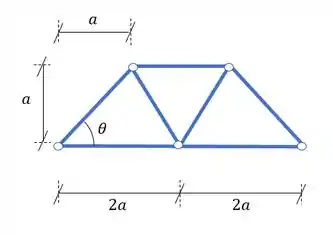
Veja que podemos determinar um triangulo retângulo no interior da treliça, agora fica fácil determinar ou o valor do ângulo ou o valor de seno e cosseno e até tangente.
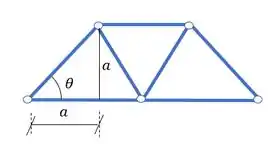
Como nesse caso temos cateto oposto e cateto adjacente iguais, sabemos que
Então nesse caso é mais fácil determinar o ângulo, que nesse caso é 45°. Em alguns casos é mais fácil determinar o seno e o cosseno, mas nesse caso é bem mais simples determinar o ângulo. Agora vamos voltar para o equilíbrio do nosso nó A.
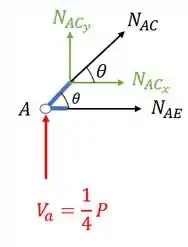
Agora que já temos o ângulo podemos decompor o nosso normal nas componentes e , dessa forma podemos escrever os nossos vetores decompostos como
Dessa forma teremos que fazer o equilíbrio da seguinte figura
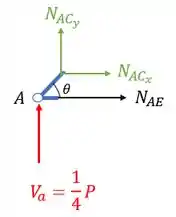
Você pode estar se perguntando, “poxa, e não estão alinhados, não deveria ter um momento nesse caso?”
Não, pois no caso isso é só uma representação para ficar mais fácil saber para onde cada normal está apontando, mas sempre se lembre que o equilíbrio é feito no nó, ou seja, exatamente em cima do nó, não há momento então. Agora chega de ladainha e vamos ao equilíbrio.
Mas já determinamos cada um desses termos, substituindo
Como já temos os valores de basta que façamos a substituição
E olha que interessante
E até aqui, aprendemos a fazer o nosso equilíbrio do nó A, para a parte 2 dessa aula, aprenderemos a fazer o equilíbrio do resto dos nós, assim como, aprenderemos a escolher o próximo nó de cálculo, vamos nessa?

Determinação do ângulo
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Abaixo foi dada uma treliça simples composta por 7 barras. Usando seus conhecimentos determine quais os melhores nós a serem iniciados e determine o valor dos normais das barras que compõem esses nós.
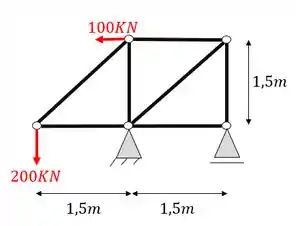
Passo 1
Para resolver os problemas sobre treliças precisamos seguir uma sequência de passos que facilita a resolução, em que temos que respeitar o seguinte
- Primeiro devemos calcular as reações de apoios da nossa treliça, que será calculada levando em consideração dois fatores
- A segunda coisa que devemos analisar nesse exercício é o melhor nó, e para isso temos que lembrar que no equilíbrio de nós sempre iremos usar as seguintes equações
- A terceira coisa que devemos ver é que sempre que resolvemos uma barra, tiramos uma incógnita do nosso problema, ou seja, se tivermos nós que compartilhem a mesma barra, pro nó ainda a ser resolvido, a barra compartilhada com ele o ajudará a calcular as desconhecidas, sempre, é claro, respeitando a regra de duas barras desconhecidas por nó, como vimos na teoria.
As reações

E as equações de equilíbrio
Ou seja, se temos duas equações, só podemos ter duas incógnitas para resolver o nosso nó.
Como cada barra representa uma incógnita, e que pelo passo anterior já teremos calculado as reações de apoio, sabemos que as únicas incógnitas serão as barras, e lembre-se, se cada barra é uma incógnita, e eu só posso ter duas incógnitas por nó, os melhores nós para iniciarmos serão aqueles que tem duas barras.
Se seguirmos esse último passo ao pé da letra, conseguiremos resolver tranquilamente todas as barras de uma treliça.
Agora que já conhecemos os três passos da nossa solução, vamos aplicar eles ao nosso problema.
Passo 2
A primeira coisa que devemos fazer como vimos no nosso passo a passo é definir as reações de apoio. Para isso devemos primeiro determinar os vetores reações de apoio e lembrar que sempre consideramos a nossa treliça como um elemento solido e único que usamos para determinar essas reações, com isso teremos que o nosso diagrama de corpo livre será
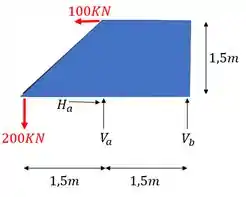
Definido os vetores reações de apoio já podemos usar as fórmulas de equilíbrio
Substituindo
Como deu negativo, sabemos que só significa que a direção do vetor que escolhemos está equivocada, ou seja, basta mudarmos a direção do vetor para ficarmos com a direção correta e assim podermos usar o sinal positivo ao invés do negativo
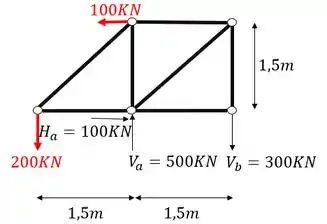
Assim já cumprimos a primeira parte do nosso passo a passo.
Passo 3
Agora que já cumprimos a primeira parte, precisamos fazer a segunda parte, que consiste em definir os melhores nós a serem calculados, e o valor do normal nas barras desses nós.
Como vimos anteriormente, os melhores nós para iniciarmos são aqueles que possuem somente duas barras, já que como vimos, cada nó só pode ter duas barras desconhecidas.
Com isso a nossa barra tem que os melhores nós que ela possui para iniciarmos os cálculos são
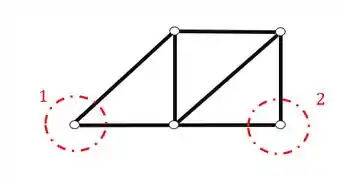
Pois são os únicos nós que possuem somente duas barras, logo, são os melhores para iniciarmos.
Passo 4
Agora precisamos fazer o equilíbrio dos nós, vamos começar pelo nó 1.
Sabemos que a primeira coisa que devemos fazer é isolar o nó como vemos abaixo

A segunda coisa que devemos fazer é colocar os normais saindo das barras cortadas
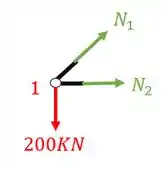
A terceira coisa que devemos fazer é definir o seno e o cosseno do ângulo entre as barras, pra isso usaremos as medidas dadas na nossa treliça
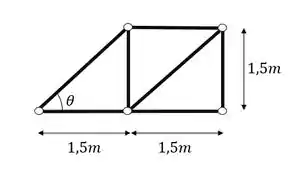
Sabemos que podemos calcular o nosso ângulo pela tangente, dessa forma teremos
Qual ângulo tem tangente igual a 1? Isso mesmo
Agora já conseguimos decompor os nossos normais, já que já temos o ângulo, vamos calcula-los então.
Passo 5
Vamos lá então, decompondo os nossos normais teremos que
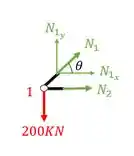
Fazendo a decomposição teremos que
Substituindo e fazendo o equilíbrio teremos que
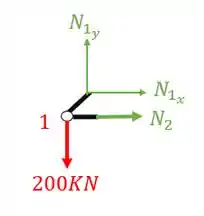
Sabemos que , substituindo teremos que
Logo
Substituindo no segundo sistema teremos
Então já calculamos os normais das barras do primeiro nó.
Passo 6
Vamos agora calcular os normais do segundo nó, sabemos que a primeira coisa que devemos fazer é isolar o nó como vemos abaixo
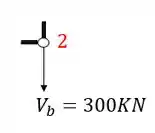
A segunda coisa que devemos fazer é colocar os normais saindo das barras cortadas
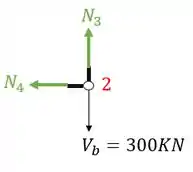
Fazendo o equilíbrio teremos que
Resposta
Os Normais são
Exercício Resolvido #2
Elaboração própria
Determine o valor do normal da barra AB e AC da treliça simples dada abaixo.
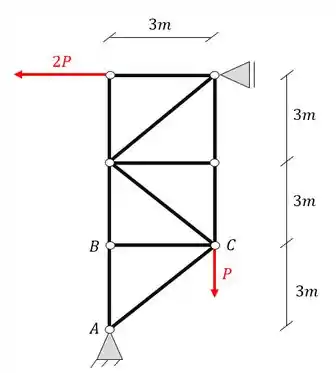
Passo 1
Para resolver os problemas sobre treliças precisamos seguir uma sequência de passos que facilita a resolução, em que temos que respeitar o seguinte
- Primeiro devemos calcular as reações de apoios da nossa treliça, que será calculada levando em consideração dois fatores
- A segunda coisa que devemos analisar nesse exercício é o melhor nó, e para isso temos que lembrar que no equilíbrio de nós sempre iremos usar as seguintes equações
- A terceira coisa que devemos ver é que sempre que resolvemos uma barra, tiramos uma incógnita do nosso problema, ou seja, se tivermos nós que compartilhem a mesma barra, pro nó ainda a ser resolvido, a barra compartilhada com ele o ajudará a calcular as desconhecidas, sempre, é claro, respeitando a regra de duas barras desconhecidas por nó, como vimos na teoria.
As reações

E as equações de equilíbrio
Ou seja, se temos duas equações, só podemos ter duas incógnitas para resolver o nosso nó.
Como cada barra representa uma incógnita, e que pelo passo anterior já teremos calculado as reações de apoio, sabemos que as únicas incógnitas serão as barras, e lembre-se, se cada barra é uma incógnita, e eu só posso ter duas incógnitas por nó, os melhores nós para iniciarmos serão aqueles que tem duas barras.
Se seguirmos esse último passo ao pé da letra, conseguiremos resolver tranquilamente todas as barras de uma treliça.
Agora que já conhecemos os três passos da nossa solução, vamos aplicar eles ao nosso problema.
Passo 2
A primeira coisa que devemos fazer como vimos no nosso passo a passo é definir as reações de apoio. Para isso devemos primeiro determinar os vetores reações de apoio e lembrar que sempre consideramos a nossa treliça como um elemento solido e único que usamos para determinar essas reações, com isso teremos que o nosso diagrama de corpo livre será
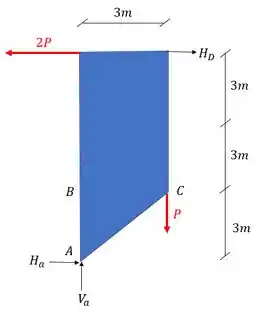
Definido os vetores reações de apoio já podemos usar as fórmulas de equilíbrio
Substituindo
Assim já cumprimos a primeira parte do nosso passo a passo.
Passo 3
Agora que já cumprimos a primeira parte, precisamos fazer a segunda parte, que consiste em definir os melhores nós a serem calculados, e o valor do normal de cada barra até que calculemos as barras pedidas no enunciado.
Como vimos anteriormente, os melhores nós para iniciarmos são aqueles que possuem somente duas barras, já que como vimos, cada nó só pode ter duas barras desconhecidas.
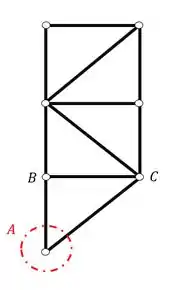
Mas perceba que o único nó que possui duas barras é exatamente o nó com as barras que precisamos calcular
Passo 4
Agora precisamos fazer o equilíbrio dos nós, vamos começar.
Sabemos que a primeira coisa que devemos fazer é isolar o nó como vemos abaixo
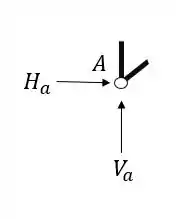
A segunda coisa que devemos fazer é colocar os normais saindo das barras cortadas
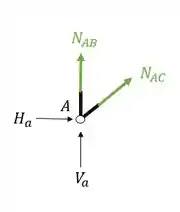
A terceira coisa que devemos fazer é definir o seno e o cosseno do ângulo entre as barras, pra isso usaremos as medidas dadas na nossa treliça
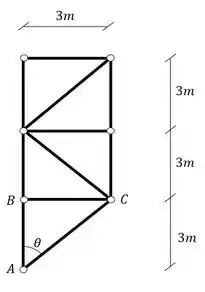
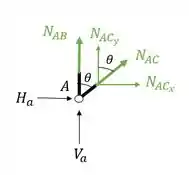
Sabemos que podemos calcular o nosso ângulo pela tangente, dessa forma teremos
Qual ângulo tem tangente igual a 1? Isso mesmo
Agora já conseguimos decompor os nossos normais, já que já temos o ângulo, vamos calcula-los então.
Passo 5
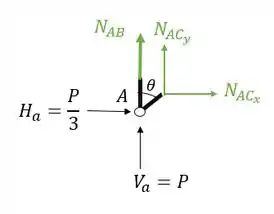
Vamos lá então, decompondo os nossos normais teremos que
Fazendo a decomposição teremos que
Substituindo e fazendo o equilíbrio teremos que
Sabemos que , substituindo teremos que
Logo
Substituindo no segundo sistema teremos
Então já calculamos os normais nas barras AB e AC
Resposta
Os Normais são
Exercício Resolvido #3
Elaboração própria
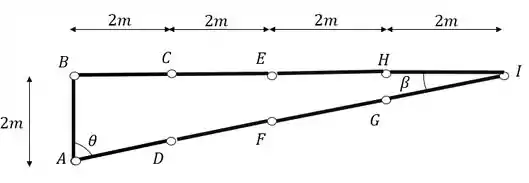
A treliça abaixo foi sujeita ao carregamento mostrado. Determine o valor do normal nas barras AB, AD, GI e HI.
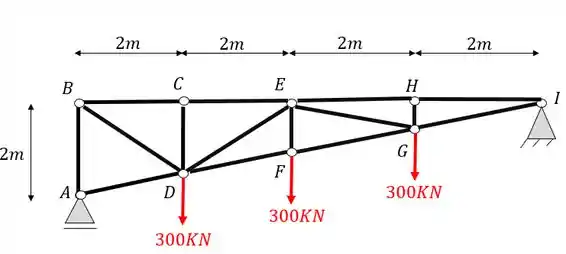
Passo 1
Para resolver os problemas sobre treliças precisamos seguir uma sequência de passos que facilita a resolução, em que temos que respeitar o seguinte
- Primeiro devemos calcular as reações de apoios da nossa treliça, que será calculada levando em consideração dois fatores
- A segunda coisa que devemos analisar nesse exercício é o melhor nó, e para isso temos que lembrar que no equilíbrio de nós sempre iremos usar as seguintes equações
- A terceira coisa que devemos ver é que sempre que resolvemos uma barra, tiramos uma incógnita do nosso problema, ou seja, se tivermos nós que compartilhem a mesma barra, pro nó ainda a ser resolvido, a barra compartilhada com ele o ajudará a calcular as desconhecidas, sempre, é claro, respeitando a regra de duas barras desconhecidas por nó, como vimos na teoria.
As reações

E as equações de equilíbrio
Ou seja, se temos duas equações, só podemos ter duas incógnitas para resolver o nosso nó.
Como cada barra representa uma incógnita, e que pelo passo anterior já teremos calculado as reações de apoio, sabemos que as únicas incógnitas serão as barras, e lembre-se, se cada barra é uma incógnita, e eu só posso ter duas incógnitas por nó, os melhores nós para iniciarmos serão aqueles que tem duas barras.
Se seguirmos esse último passo ao pé da letra, conseguiremos resolver tranquilamente todas as barras de uma treliça.
Agora que já conhecemos os três passos da nossa solução, vamos aplicar eles ao nosso problema.
Passo 2
A primeira coisa que devemos fazer como vimos no nosso passo a passo é definir as reações de apoio. Para isso devemos primeiro determinar os vetores reações de apoio e lembrar que sempre consideramos a nossa treliça como um elemento solido e único que usamos para determinar essas reações, com isso teremos que o nosso diagrama de corpo livre será
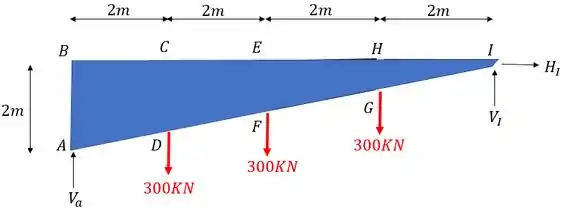
Definido os vetores reações de apoio já podemos usar as fórmulas de equilíbrio
Substituindo
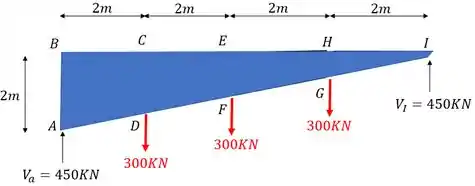
Assim já cumprimos a primeira parte do nosso passo a passo.
Passo 3
Agora que já cumprimos a primeira parte, precisamos fazer a segunda parte, que consiste em definir os melhores nós a serem calculados, e o valor do normal nas barras desses nós.
Como vimos anteriormente, os melhores nós para iniciarmos são aqueles que possuem somente duas barras, já que como vimos, cada nó só pode ter duas barras desconhecidas.
Com isso a nossa barra tem que os melhores nós que ela possui para iniciarmos os cálculos são
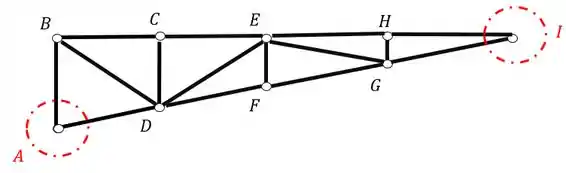
Pois são os únicos nós que possuem somente duas barras, logo, são os melhores para iniciarmos, e perceba o seguinte, esses dois nós possuem exatamente as barras que precisamos calcular, ou seja, fazer o equilíbrio deles nós permitirá calcular exatamente as barras que são pedidas no problema. Vamos calcula-las então.
Passo 4
Agora precisamos fazer o equilíbrio dos nós, vamos começar pelo nó A.
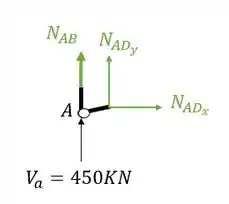
Sabemos que a primeira coisa que devemos fazer é isolar o nó como vemos abaixo
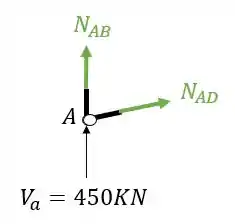
A segunda coisa que devemos fazer é colocar os normais saindo das barras cortadas
A terceira coisa que devemos fazer é definir o seno e o cosseno do ângulo entre as barras, pra isso usaremos as medidas dadas na nossa treliça
Sabemos que podemos calcular o nosso ângulo pela tangente, dessa forma teremos
Qual ângulo tem tangente igual a 4?
Agora já conseguimos decompor os nossos normais, já que já temos os ângulos, vamos calcula-los então.
Passo 5
Vamos lá então, decompondo os nossos normais teremos que
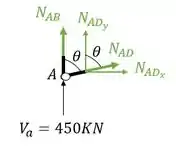
Fazendo a decomposição teremos que
Substituindo e fazendo o equilíbrio teremos que
Sabemos que , substituindo teremos que
Logo
Substituindo no segundo sistema teremos
Então já calculamos os normais das barras do nó A.
Passo 6
Vamos agora calcular os normais do segundo nó, o nó I , sabemos que a primeira coisa que devemos fazer é isolar o nó como vemos abaixo
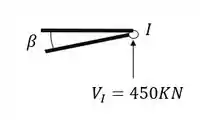
A segunda coisa que devemos fazer é colocar os normais saindo das barras cortadas
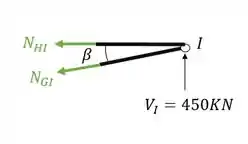
Agora já conseguimos decompor os nossos normais, já que já temos os ângulos, vamos calcula-los então.
Passo 7
Vamos lá então, decompondo os nossos normais teremos que
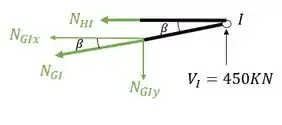
Fazendo a decomposição teremos que
Substituindo e fazendo o equilíbrio teremos que
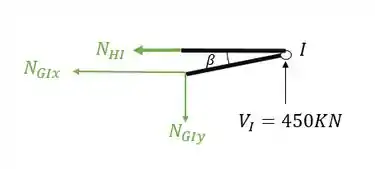
Sabemos que , substituindo teremos que
Logo
Substituindo no segundo sistema teremos
Então já calculamos os normais das barras do nó I.
Resposta
Os Normais são
Exercício Resolvido #4
PUC Minas – Atividade 12
Verifique os valores das trações, compressões e reações de apoio na treliça abaixo e preencha a tabela.
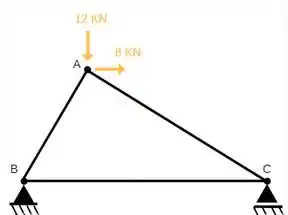
Dados : AB = 3 m, BC = 6 m e Ângulo(abc) = 60°
Passo 1
Vamos entender o enunciado...
De acordo com enunciado, precisamos encontrar todas as forças em todas as barras.
Para isso agora precisamos determinar, quais são as reações existentes na treliça! Boraaa?
Começamos, desenhando em vermelho todas as reações existentes que são realizadas pelos apoios. São elas:
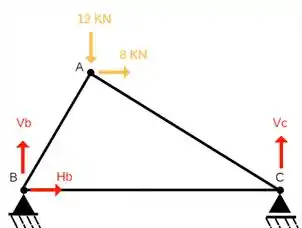
Não se esqueça, quando temos um apoio de primeiro gênero como o do ponto C, temos apenas esforço na vertical e quando temos um apoio de segundo gênero como o do ponto B, teremos esforço na horizontal e na vertical!Mais uma dica importante, você pode arbitrar a o sentido das forças como achar melhor ou até mais bonitinho, rs!
Pois caso você escolha uma direção e ela esteja errada, você vai encontrar no final o resultado com uma resposta negativa, e na mecânica resultados negativos caracterizam, que a direção é ao contrário do que arbitrou inicialmente!
Agora, podemos verificar a Isostática da treliça, segundo a fórmula:
Onde n = 3 pois temos os nós A,B e C;
b = 3, pois temos três barras;
v = 3, pois temos três reações nos apoios.
Assim,
Passo 2
Agora é a hora calcular as reações de apoio.
Vamos usar as condições para a treliça estar em equilíbrio, lembrando são elas;
Antes, podemos observar que essa treliça tem o formato de um triângulo retângulo de 30°, 60° e 90°, pois AB é a metade de BC com um ângulo de 60° entre eles. Essa dica pode facilitar as contas pois agora sabemos que a medida de AC:
Utilize a ideia também que como esse triângulo é retângulo, a altura A até a barra BC, tem medida , e que a distância horizontal desde mesmo ponto é . Essa conta será utilizada para o cálculo no somatório dos momentos.
Somatório dos momentos em relação ao ponto B igual a zero!
-
Somatório das forças verticais igual a zero!
Somatório das forças Horizontais igual a zero!
Passo 3
Agora iremos Anlisar cada Nó da treliça.
Vamos começar analisando o nó A;
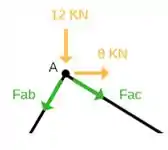
Somatório das forças Horizontais igual a zero!
Somatório das forças verticais igual a zero!
Podemos isolar Fab na primeira expressão:
Substituindo na segunda expressão:
Assim,
Agora basta escolhermos um dos nós para encontrar todas as forças!
Escolhemos o ponto C por ter menos reações:
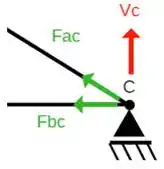
Somatório das forças Horizontais igual a zero!
Assim conseguimos encontrar todos os resultados das forças nas barras!
Resposta
Exercício Resolvido #5
UFF – Professora Salete - Número 3
Determine a força em cada elemento da treliça mostrada na Figura abaixo. Indique se os elementos estão sobre tração ou compressão.
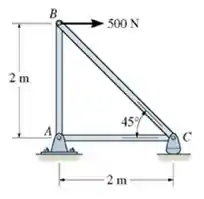
Passo 1
Bom, precisamos começar entendendo o enunciado,
Para esse exercício precisaremos calcular todas as reações a fim de entender quais elementos estão sobre tração e quais sobre compressão. Além disso, precisamos entender quais são as reações nos apoios.
No apoio no ponto A existem uma reação Ax e uma reação Ay, visto que temos um apoio de segundo gênero.
Já no apoio no ponto C existe apenas uma reação Cy, visto que temos um apoio de primeiro gênero.
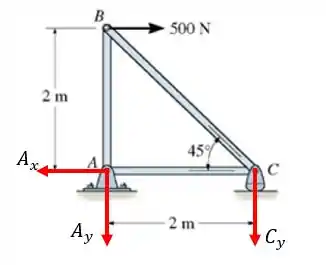
Passo 2
Agora é a hora calcular as reações de apoio.

Vamos usar as condições para a treliça estar em equilíbrio, são elas;
Somatório dos momentos em relação ao ponto C igual a zero. Aqui vamos fazer o somatório dos momentos em relação à para podermos eliminar tanto o termo quanto o termo .
Somatório das forças verticais igual a zero:
Somatório das forças horizontais igual a zero:
Passo 3
Agora podemos analisar cada Nó da treliça.
Vamos começar analisando o nó A;
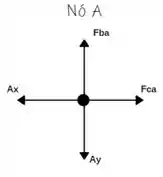
Somatório das forças horizontais igual a zero:
Somatório das forças verticais igual a zero:
;
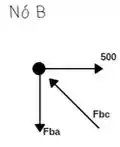
Somatório das forças horizontais igual a zero:
Somatório das forças verticais igual a zero:
Agora vamos analisar o nó C;
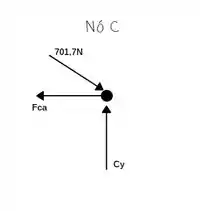
Somatório das forças horizontais igual a zero:
Somatório das forças verticais igual a zero:
Com todas as reações computadas, chegamos a seguinte resposta:
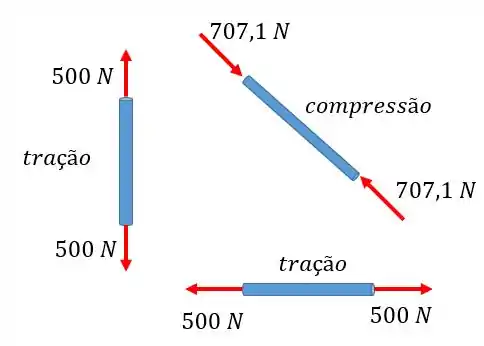
Resposta
Barra AC (Tração)Barra AB (Tração)Barra BC (Compressão)
Exercício Resolvido #6
Prova UNEMAT (Universidade do Estado do Mato Grosso) - Professor Cassio Simioni – Questão 5
Considere a treliça abaixo como isostática. Calcule o valor dos esforços normais de todas as barras, utilizando o método dos nós, indicando o correspondente em KN para cada barra. Na questão, para cada realização do DCL dos nós, será descontada uma pontuação de 0,2.
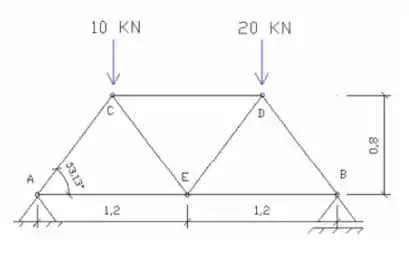
Passo 1
Como o nosso enunciado já diz, precisaremos determinar os esforços em cada barra! Certo?Mais ou menos né... Pois, dessa vez o professor foi um pouco mais maldoso!
Nessa prova o intuito dele, era testar se os alunos conseguiriam realizar a separação de cada nó sem o auxílio dos desenhos, ou seja sem o DCL (Diagrama de Corpo Livre)!
Só que ele não contava com a gente, rs e vamos ver que é possível fazer o exercício sem os DCL’s.Então bora lá usar o método dos nós sem os DCL’s , tenho certeza que a gente consegue...

Primeiro precisamos vamos verificar quais são os valores das reações dos apoios! Antes vamos estipular o seguinte, só entre nós, se as forças estiverem para esquerda ou para baixo elas vão ganhar um sinal negativo, se as forças estiverem para direita ou para cima , vão ganhar um sinal positivo ok? Isso vai salvar muito nossa vida!No nó A tempos um apoio de segundo gênero, dessa forma teremos uma força na horizontal e uma na vertical (Ax e Ay) e no nó B temos um apoio de primeiro gênero, com uma única reação na vertical (By).Dessa forma, podemos agora determinar o valor das reações.
Somatório dos momentos em relação ao ponto A:
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 2
Vamos pensar no isolamento do ponto A na treliça;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 3
Próximo nó que podemos isolar é o nó C;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 4
Próximo nó que podemos isolar é o nó E;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 5
Próximo nó que podemos isolar é o nó D;
Somatório das forças horizontais iguais a zero:
Passo 6
Próximo nó que podemos isolar é o nó B;
Somatório das forças horizontais iguais a zero:
Resposta
Todas as forças positivas são forças de tração e todas as forças negativas são forças de compressão.