Exercícios Resolvidos de Medidas de Centralidade e Dispersão para Dados Agrupados
Ver TeoriaEnunciado
Considerando os dados abaixo:
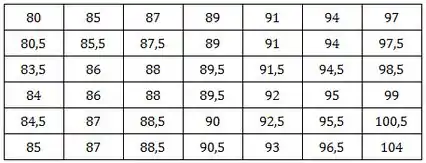
- Construa a distribuição de frequência para dados grupados (utilizando Sturges);
- Encontre a amplitude total;
- Calcule a média;
- Calcule a mediana;
- Calcule a moda;
- Calcule a variância;
- Calcule o desvio padrão;
- Calcule o coeficiente de variação.
Passo 1
(a)
Aqui nós montaremos uma tabelinha de distribuição de frequência assim como fazíamos para os dados, a diferença é que aqui agruparemos os dados para montar!
Então, a primeira coisa que faremos como queremos dados agrupados, é dividir os valores em classes.
O exercício pede pra usarmos a regra da Sturges. Como vimos lá na teoria, a fórmula para essa regra é:
Onde é o número de elementos da nossa amostra e a quantidade de classe que vamos ter! Se a gente tem 42 valores na amostra:
Arredondando isso aí, vamos ter então 6 classes.
Passo 2
(b) Agora precisamos calcular a amplitude da nossa amostra.
Reparem que a nossa tabela já tá em ordem crescente! A diferença aqui é que tá crescendo “pra baixo”, no sentido das colunas, e não das linhas.
Então podemos ver de cara que o maior valor que temos é 104 e o menor é 80.
A amplitude total da amostra é então:
Com isso, cada classe vai ter uma amplitude igual a:
Ou seja vamos ter classes de 4 em 4, começando por 80.
Passo 3
Para construir a distribuição de frequência vamos montar uma tabela com as seguintes colunas:
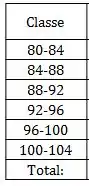
Vamos ver como fica para a nossa primeira classe, que vai começar em e como , vai terminar em . Nossos valores entre e são:
Lembrem que nunca contamos o valor que “fecha” o intervalo, no nosso caso o .
Vamos calcular as informações dessa primeira classe então. Começando pelo valor médio . Se a classe vai de a , o valor médio é:
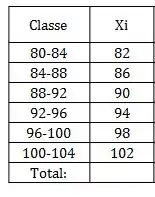
Agora a frequência absoluta da classe, ou seja, quantos elementos temos dentro dela. Por exemplo,
Só ir somando as anteriores;
No primeiro caso
Por quê? Porque essa é nossa primeira classe, então não temos nenhuma frequência acumulada para somar a ela, por que não há classes antes dela!
No caso
E vamos seguir esse mesmo processo pro restante! Ficaremos com
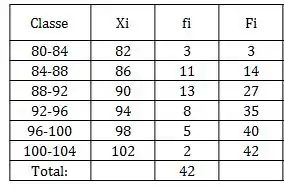
Que é dividir pelo total de valores que no caso são 42;
Por exemplo, na primeira classe a frequência relativa vai ficar:
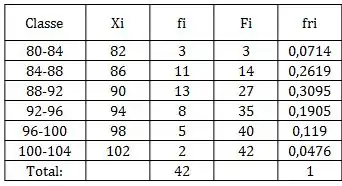
Que é dividir pelo total de valores (42). Para a primeira classe, teriamos
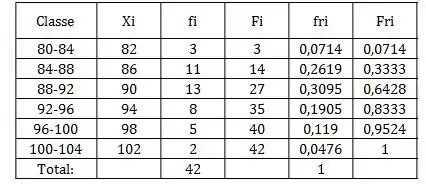
Passo 4
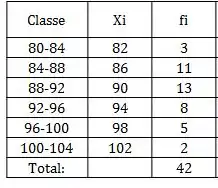
Repetindo esse passo a passo para todas as classes, ficaria algo assim:
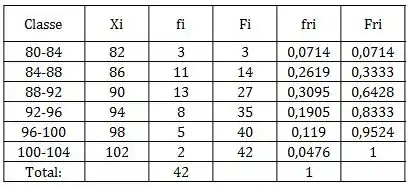
Passo 5
(c)
Para dados grupados calculamos a média usando:
Passo 6
(d)
Pra calcular a mediana, temos primeiro que identificar a classe da mediana.
Para isso calculamos o valor de que será .
Agora, olhando para os valores de procuramos em qual classe estará o valor 21. Percebemos que a classe tem . Como queremos 21 não usaremos essa e sim a seguinte.
No nosso caso a classe da mediana será .
Ai usamos a fórmula:
Onde
limite inferior da classe que contém a mediana.
frequência acumulada anterior à classe que contém a mediana.
frequência dessa classe.
amplitude da classe
Assim,
Passo 7
(e)
Para calcular a moda, temos primeiro que achar a classe modal que é a classe com a maior frequência absoluta.
No casso é a classe que tem .
Aí usamos a fórmula:
Onde
limite inferior da classe modal
frequência da classe modal menos a da classe anterior
frequência da classe modal menos a da classe posterior
amplitude da classe
Passo 8
(f)
Para a variância vamos usar a fórmula:
Passo 9
(g)
Desvio padrão:
Passo 10
(h)
Coef. De variação:
Resposta
Ei, a resposta está no passo a passo :)