Exercícios Resolvidos de Medidas de Centralidade e Dispersão para Dados Agrupados
Ver TeoriaEnunciado
A distribuição de frequências do número de apreensões de valores (em milhões R$) realizadas pela Polícia Federal, em determinado período, é conforme a seguir:
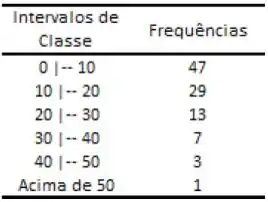
Assim sendo, é correto afirmar que:
A) o último Decil está na penúltima classe;
B) a mediana da distribuição está na 2ª classe;
C) a média da distribuição está na 3ª classe;
D) a distribuição é assimétrica à esquerda.
Passo 1
Nessa questão, vamos avaliar cada um dos itens e ver qual é o verdadeiro e quais são falsos!
A letra A), diz que o último Decil está na penúltima classe. Vamos encontrar então quem é o nosso último Decil.
O Decil nada mais é do que o elemento que divide os nossos dados em grupos de , por isso, o primeiro Decil é o dado que representa o valor na posição de 10%, o segundo Decil o valor na posição de 20%, o quinto Decil, por exemplo, é o valor na posição de 50% que é o mesmo valor que a mediana!Nós temos um total de nove decis, e o último decil é o elemento que representaria a posição de 90%.
Somando todos as frequências, temos um total de:
Opa! Aí tá fácil né, como temos 100 dados, o último decil vai ser exatamente o dado da posição 90.
Fazendo a frequência acumulada por classes, vemos que:
A classe 1 vai do dado 1 até o dado 47.
A classe 2 vai do dado 48 até o dado ().
A classe 3 vai do dado 77 até o dado ().
Opa, o nosso último decil então está na classe 3, que não é a penúltima classe, logo essa está errada.
Passo 2
A letra b), diz que a mediana se encontra na segunda classe.
A mediana acontece na posição de que nesse caso aonde temos 100 dados, será o dado de número .
E essa posição acontece justamente ali na 2ª classe, certo? Já que a frequência acumulada da 2ª classe é , e a primeira classe tem itens, todos os dados entre e vão pertencer a 2ª classe!
Então a resposta é a letra B).
Passo 3
A letra c), diz que a média da distribuição está na terceira classe.
Média aritmética
Para dados agrupados usaremos:
Ou seja,
E podemos ver que a segunda classe tem um intervalo de valores entre e , por isso a média está na segunda classe e não na terceira, por isso está errada.
Passo 4
Na letra D), diz que a distribuição é assimétrica a esquerda.
Isso vai ocorrer quando a moda for maior que a mediana.
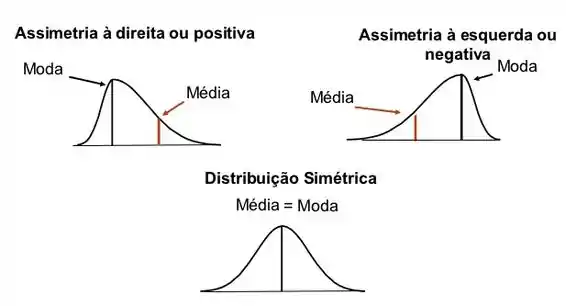
(Se a moda for igual a mediana, a distribuição é simétrica e se for menor é assimétrica a direita.)
Vamos encontrar aonde está nossa moda, então!
Temos que a classe com maior frequência é a primeira classe, logo a moda ocorre nessa classe e por isso é menor que a média (que ocorre na segunda classe).
Sendo assim, essa é uma distribuição assimétrica à direita e não à esquerda e essa alternativa D) está errada.
Por fim, a única alternativa correta é a letra B).
Resposta
Letra B)