Considere a curva de reação a uma perturbação degrau unitário mostrada abaixo. 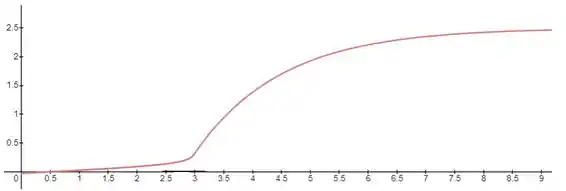
Para esse processo, sintonize um controlador P, PI e PID utilizando as correlações de Cohen-Coon.
Passo 1
Primeiramente, vamso tentar achar a função de primeira ordem com tempo morto aproximada que melhor descreve o processo da figura. Essa função, terá o seguinte formato:
Então precisamos determinar os parâmetros , e através do gráfico da curva de reação. A forma de se obter esses valores está mostrada no exemplo genérico abaixo:
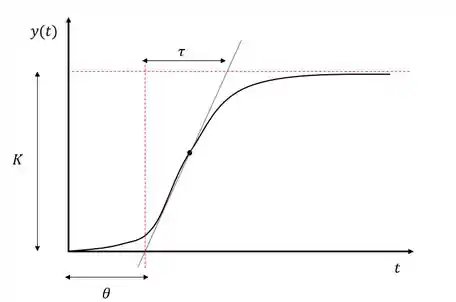
Passo 2
Para facilitar a nossa visualização, vamos fazer alguns traços para ficar mais fácis de enxergar os pontos que precisamos.
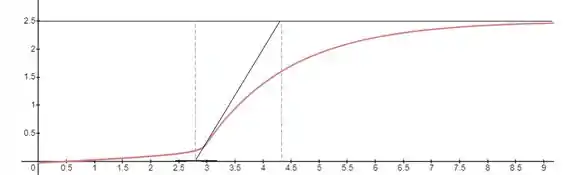
Agora a gente já pode estimar as nossas constantes para conseguir fazer a sintonização:
E a função FOPDT ficará:
Antes de sintonizar os três controladores, precisamos primeiro verificar se realmente o método de Cohen-Coon é apropriado para o sistema do exercício.
O método de Cohen- Coon é indicado para a seguinte faixa:
Para o nosso processo temos:
Logo, está dentro da faixa, e pode ser sintonizado por Cohen-Coon
Passo 3
Agora só nos resta aplicar as correlações propostas por Cohen-Coon que estão na tabela abaixo:

Primeiramente, vamos fazer a sintoniza para um controlador puramente proporcional:
Pela tabela:
Portanto, o controlador P terá função de transferência:
Passo 4
Para sintonizar um controlador PI, usaremos as fórmulas da segunda linha da tabela. O controlador PI tem a seguinte função de transferência padrão:
Aplicando as correlações de Cohen-Coon:
Sendo assim, teremos a seguinte FT para um controlador PI:
Passo 5
Por fim, vamos sintonizar um controlador PID para o processo:
Usando as correlações da última linha da tabela:
Portanto, o nosso controlador PID ficará com a seguinte FT:
Resposta
Controlador P:
Controlador PI:
Controlador PID: