Para o sistema representado pela curva de reação ao degrau abaixo, utiliza o método de Cohen-Coon para sintonizar um controlador PI.
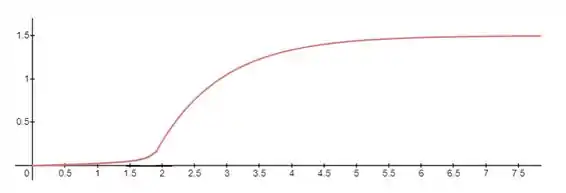
Passo 1
Para aplicar o método de Cohen-Coon, devemos aproximar o processo a uma função de transferência de primeira ordem com tempo morto (FOPDT), conforme o modelo abaixo:
Para isso, devemos conseguir os parâmetros , e da imagem utilizando o método ma máxima tangente. A forma de se obter esses valores está mostrada no exemplo genérico abaixo:
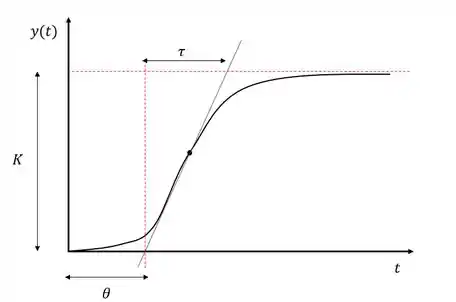
Passo 2
Vamos aplicar o método no nosso processo então:
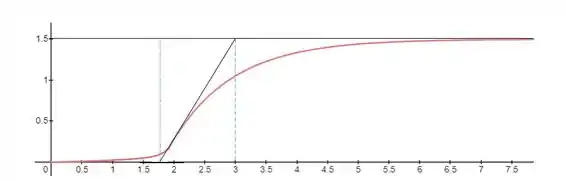
Com esse esboço, podemos estimar nossas constantes como:
E a função FOPDT ficará:
Antes de fazer a sintonização, vamos checar se o processo pode ser sintonizado pelo método de Cohen-Coon.
O método de Cohen- Coon é indicado para a seguinte faixa:
Para o nosso processo temos:
Logo, está dentro da faixa, e pode ser sintonizado por Cohen-Coon
Passo 3
Agora só nos resta aplicar as correlações propostas por Cohen-Coon que estão na tabela abaixo:

Como queremos um controlador PI, vamos utilizar as fórmulas da segunda linha:
Portanto, o nosso controlador terá função de transferência: