Dada a curva de reação para um distpurbio degrau no setpoint mostrada abaixo, sintonize um controlador PID pelo método de Cohen-Coon e pelo método de IAE mínimo.
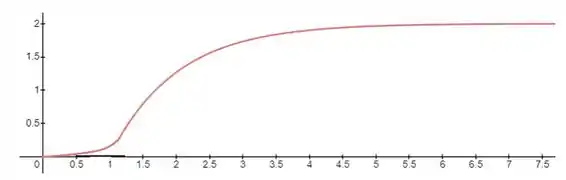
Passo 1
O primeiro passo, será definir os parâmetros da função FOPDT que melhor aproxima o sistema:
Como foi nos dados a curva de reação do sistema, nós podemos definir os parâmetros da função FOPDT como mostrado no exemplo abaixo:
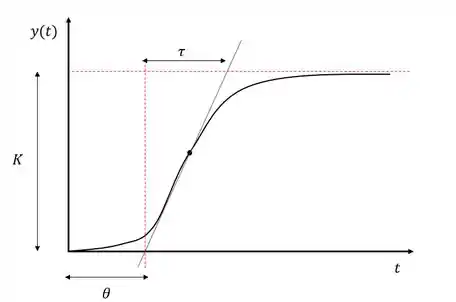
Passo 2
Vamos então encontrar as nossas três constantes:
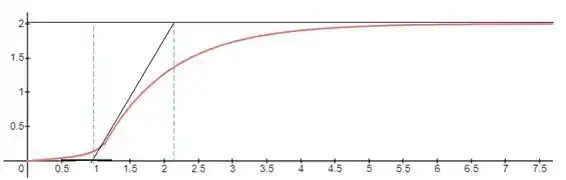
O ganho, , é a variação total da resposta, nesse caso, teremos:
O tempo morto, ou atraso, , é o ponto onde a tangente com maior inclinação cruza o valor da resposta inicia, pelo gráfico podemos ver que:
E a constantate de tempo, , é a diferença entre o ponto que a tangente de maior inclinação cruza o valor final e o ponto em que ela cruza o valor inicial, nesse caso:
A função FOPDT que aproxima o processo será:
Vamos agora, conferir se os parâmetros estão dentro da faixa que precisamos.
O método de Cohen-Coon é indicado para processos com atraso considerável, mais precisamente, a faixa inidaca é:
Já o método IAE é indicado para a seguinte faixa:
Para o nosso processo temos:
Portanto, atende às especificações de ambos os métodos. Vamos então fazer as sintonizações.
Passo 3
Primeiramente, vamos fazer para o método de Cohen-Coon utilizando as correlações da tabela abaixo:

Como queremos um PID, usaremos as correlações da terceira linha.
E a função de transferência do controlador será:
Passo 4
Vamos agora aplicar as correlações do método IAE para perturbações no setpoint.

Como queremos um controlador PID, vamos usar a última linha da tabela:
Portanto:
Passo 5
Resposta
Para o método de Cohen-Coon:
Para o método de IAE mínimo: