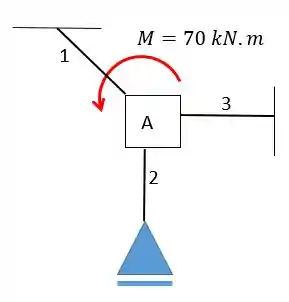
Para o nó abaixo determine o momento em cada uma das barras utilizando o método de distribuição de momentos sabendo que um momento externo atua sobre o nó A. Considere e os comprimentos das barras iguais a , e .

Passo 1
Essa questão pede para acharmos os momentos distribuídos nas barras 1,2 e 3. Todas conectadas ao nó . Para isso vamos considerar o nó um ponto de engaste, essa é a primeira coisa a ser feita.
Depois vamos utilizar a tabela de grandezas auxiliares para barras com inércia constante para achar as constantes de rigidez de cada barra. Com essas constantes vamos achar o coeficiente de distribuição. Lembrando que o coeficiente de distribuição é igual à constante de rigidez da barra sobre a soma das constantes:
Com o coeficiente de distribuição vamos achar os momentos distribuídos pelas barras =D
Passo 2
Vamos transformar então o nó num engaste, representamos isso por um simples quadrado:
Agora vamos olhar a tabela a qual o problema se refere:
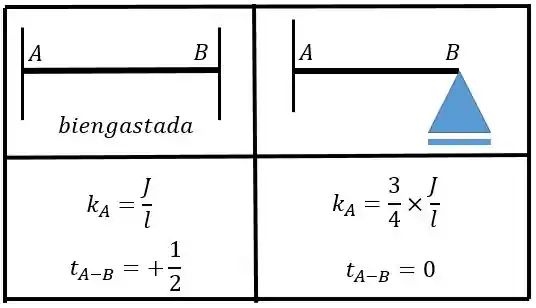
Perceba que quando temos ambos os lados engastados temos que a rigidez relativa vale:
E quando um lado é engastado e outro rotulado:
Comoas barras 1 e 3 são engastadas vamos ter:
E para a barra 2 vamos ter um lado rotulado e outro engastado então temos:
Passo 3
Com os coeficientes de rigidez relativa vamos poder calcular os coeficientes de distribuição, que é a parte mais essencial desse problema! Lembrando que:
Temos de fazer isso para cada nó envolvido, como há apenas um nó:
obs: Aqui aproximamos para duas casas decimais beleza, pessoal?
Repare que a soma de todos esses valores da 1. Isso sempre vai acontecer dentro um nó, porque o momento deve ser distribuído entre todos eles e não pode faltar nem sobrar nada.
Agora vamos representar esses termos em cada nó da seguinte forma:
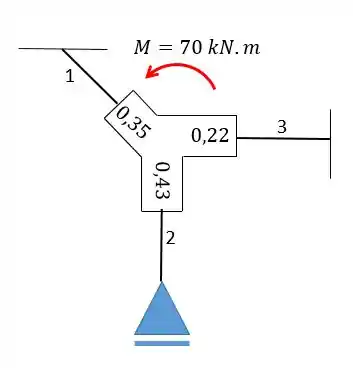
Passo 4
Finalmente vamos pegar o momento e fazer a distribuição.
Assim vamos calcular para a barra 1:
Para a barra 2:
Para a barra 3:
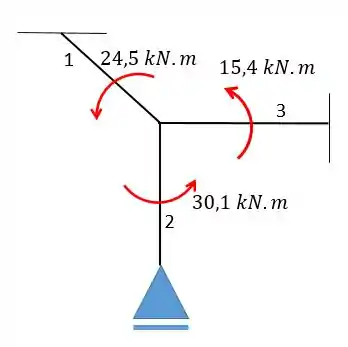
Representando num esquema:

Perceba que mantivemos o mesmo sentido do momento original e o seu módulo, já que a soma de todos esses momentos distribuídos vale .
Fim da questão =D
Resposta