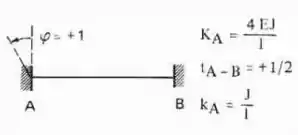
Para o carregamento e a estrutura abaixo encontre os momentos atuantes nos pontos A, B, C e D utilizando o método de Cross.
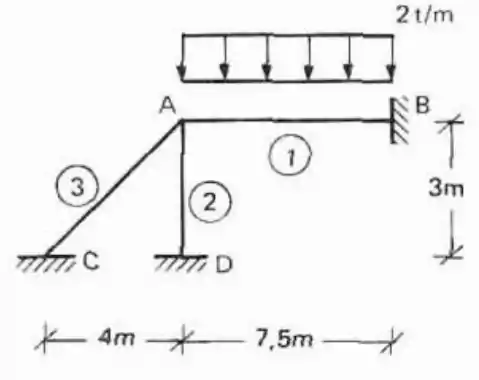
Passo 1
Essa questão pede para acharmos os momentos autantes nas barras, mais precisamente nos pontos dados.
Ao analisar a estrutra nós percebemos que se trata de uma estrutura hiperestática, ou seja, não pode ser resolvida utilizando aquelas equações da estática (somatório das forças e momentos).
Para resolver o exercício pelo método de Cross a gente vai fazer o seguinte passo a passo:
- Substituir o nó por um sistema engastado e com auxílio da tabela de momentos especificar o momento aplicado na barra , sujeita à carga.
- Calcular os coeficientes de distribuição entorno do nó.
- Aplicar o somatório dos momentos em relação ao ponto A “liberando” esse ponto, observando que o momento depende de fatores geométricos e materiais das barras.
- Calcular os momentos de cada barra segundo os fatores acima apresentados.
Passo 2
A primeira coisa que a gnete faz é a substituição do nó pelo sistema engastado, como se todas três barras estivessm biengastadas mesmo! Podemos representar isso por um quadrado em :
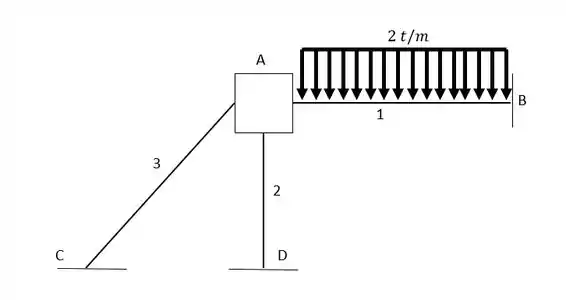
Vamos então olhar na tabela de “Grandezas auxiliares para battas com inércia constante J” e achar o momento. Como temos o caso de uma viga biengastada vamos ter:
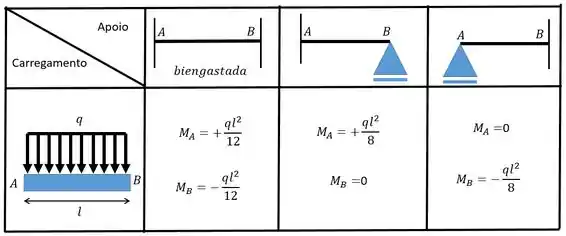
Logo o momento atuante na barra 1 será igual a :
Substituindo os valores:
Perceba então que a barra exerce um momento de sobre o ponto .
Passo 3
Os coeficientes de distribuição são os coeficientes que dizem quanto da carga-momento é aplicada em cada barra e são calculados como:
Onde é a rigidez relativa de cada barra. Esse valor da rigidez relativa também é encontrado numa tabela de “Grandezas auxiliares para barras com inércia constante ”. Retirando o caso da viga biengastada da tabela temos:
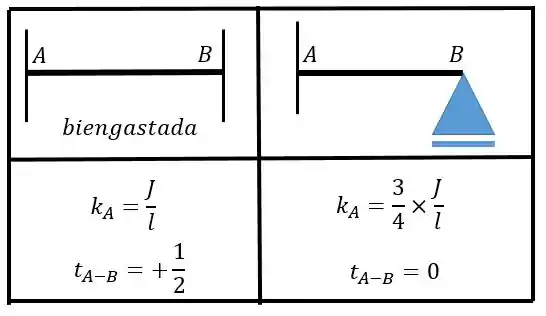
Observe que necessitamos apenas do termo . Agora vamos calcular a rigidez relativa de cada barra (lembrando que todas estão biengastadas), o valor de foi dado no problema e é o comprimento da barra:
(Para esse última caso achamos por meio de pitágoras, ok)!?
Então como temos todos os agora podemos achar o termo de cada barra:
Agora a gente coloca esses dados em conjunto com os momentos e no nosso desenho da seguinte forma:
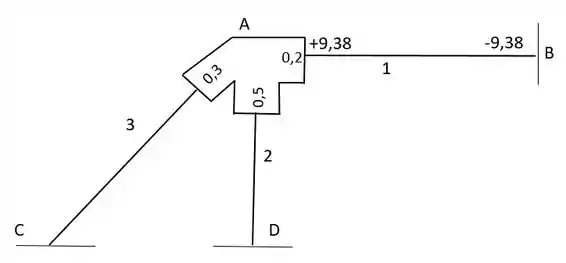
Passo 4
Agora vamos “liberar” o ponto do engaste e ao fazermos isso o momento se tornará uma carga-momento aplicado em e cada barra aplicará um momento e . Vai ficar mais ou menos assim:
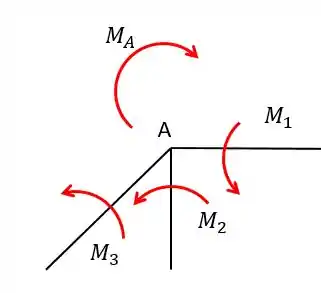
obs: Repare bem nos sentidos! O sentido horário é positivo e o anti-horário é negativo, isso é muito importante porque as tabelas que utilizamos utilizam as mesmas convenções de sentido!
Agora nós vamos aplicar a relação entre os momentos das barras , e ; essa relação é da seguinte forma:
Onde é a carga-momento (nesse caso igual a ) e é um fator que diz quanto de será aplicado numa barra . Como já calculamos o ficar fácil achar os momentos:
Pronto! Agora temos os momentos que atuam em cada barra! Repare que os valores são negativos porque estão no sentido anti-horário!
Passo 5
Mas a gente achou diversos momentos que atuam nos pontos, o importante na análise do problema é achar o momento fletor resultante. Para isso a gente vai deduzir algumas parcelas, perceba que que para as barras e não precisamos fazer isso, apenas para a barra AB, que vamos ter:
Assim vamos obter o seguinte:
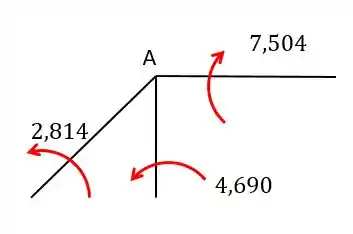
Esses são os momentos imediatamente próximos do ponto , nós precisamos também dos momentos relacionados aos pontos , e . Que são achados utilizando novamente a tabela de “Grandezas auxiliares para barras com inércia constante ”. Retirando o caso da viga biengastada da tabela temos:
Olha para o termo esse termo é chamado de coeficiente de transferência e é o termo que diz quanto do momento em vai ser transferido para . No nosso caso todos são iguais a então para as barras e basta dividir por :
Para a barra precisamos considerar também o momento que vem do engaste
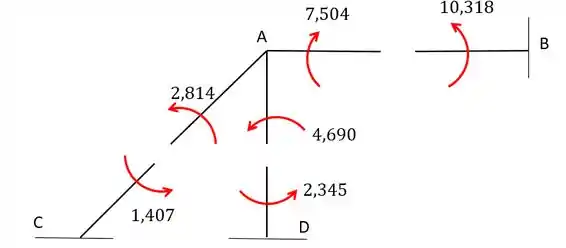
Colocando no diagrama vamos ter:
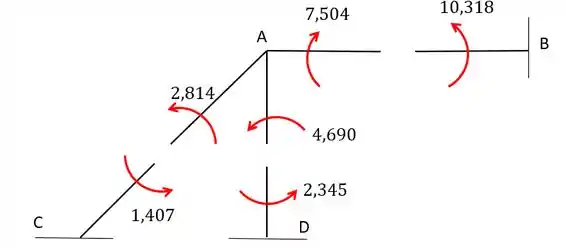
Resposta