Para o sistema abaixo encontre o valor dos momentos nos pontos B, C e D. Considere e os comprimentos das barras iguais a , e .
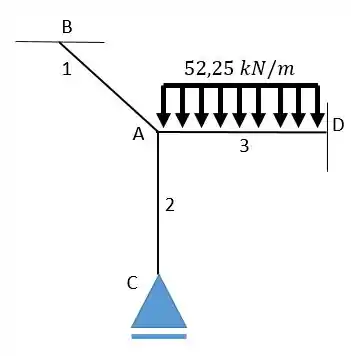
Passo 1
Essa questão pede para acharmos os momentos nos pontos A, B e C; ou seja, os pontos de apoio do sistema. Para isso vamos considerar o nó um ponto de engaste, essa é a primeira coisa a ser feita. Em seguida vamos utilizar a tabela de engastamento perfeito para saber qual será o momento gerado por esse carregamento.
Depois vamos utilizar a tabela de grandezas auxiliares para barras com inércia constante para achar as constantes de rigidez de cada barra. Com essas constantes vamos achar o coeficiente de distribuição. Lembrando que o coeficiente de distribuição é igual à constante de rigidez da barra sobre a soma das constantes:
Com o coeficiente de distribuição vamos achar os momentos distribuídos pelas barras =D
Por fim vamos aplicar o coeficiente de transmissão que nos motrará qual será o momento efetivo nos apoios!
Passo 2
Vamos transformar então o nó num engaste, representamos isso por um simples quadrado:
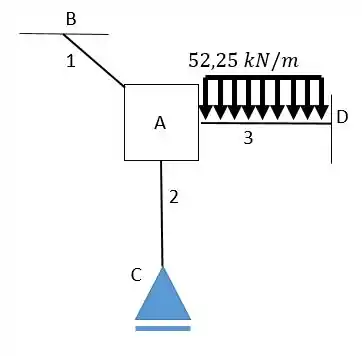
Agora vamos descobrir quanto de momento essa carga irá gerar, através da tabela de engastamento perfeito:

Perceba que temos o caso de biengastamento então vamos ter para :
E para
Calculando esses valores:
E para :
Ou seja podemos transformar esse problema em um análogo:
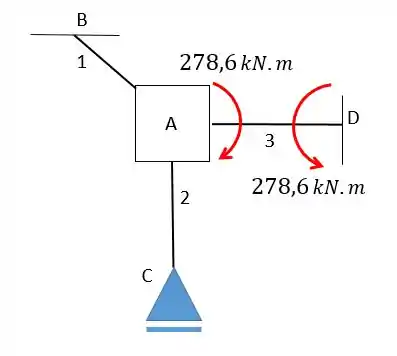
Reparem que quando temos um valor negativo de momento o sentido fica anti-horário!
Passo 3
Pessoal, esse problema ficou muito parecido com o problema da questão 1 não é mesmo? Então vamos prosseguir da mesma maneira, a única coisa que vai mudar é o sentido do momento.
Agora vamos olhar a tabela de grandezas auxiliares para barras com inércia constante afim de poder calcular o coeficiente de distribuição:
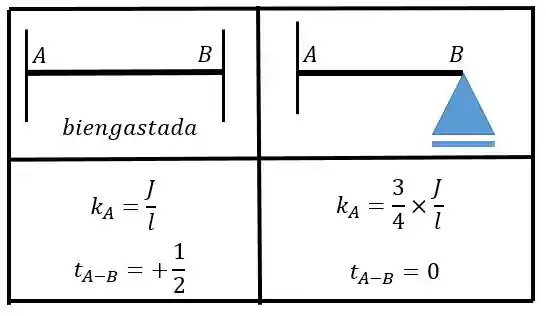
Perceba que quando temos ambos os lados engastados temos que a rigidez relativa vale:
E quando um lado é engastado e outro rotulado:
Comoas barras 1 e 3 são engastadas vamos ter:
E para a barra 2 vamos ter um lado rotulado e outro engastado então temos:
Passo 4
Com os coeficientes de rigidez relativa vamos poder calcular os coeficientes de distribuição, que é a parte mais essencial desse problema! Lembrando que:
Temos de fazer isso para cada nó envolvido, como há apenas um nó:
obs: Aqui aproximamos para duas casas decimais beleza, pessoal?
Repare que a soma de todos esses valores da 1. Isso sempre vai acontecer dentro um nó, porque o momento deve ser distribuído entre todos eles e não pode faltar nem sobrar nada.
Agora vamos representar esses termos em cada nó da seguinte forma:
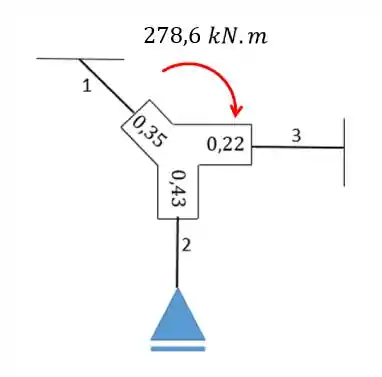
Passo 5
Finalmente vamos pegar o momento e fazer a distribuição.
Assim vamos calcular para a barra 1:
Para a barra 2:
Para a barra 3:
Representando num esquema:
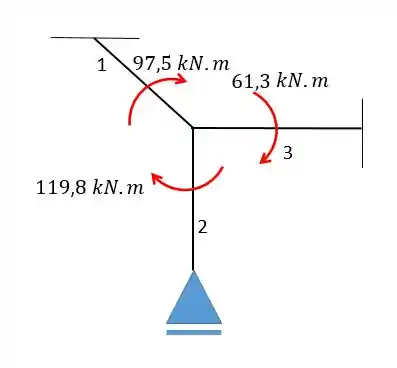
Perceba que mantivemos o mesmo sentido do momento original e o seu módulo, já que a soma de todos esses momentos distribuídos vale .
Até aqui foi bem parecido com o problema anterior. Mas além da carga distribuída vamos olhar como esses momentos em torno do nó serão distribuídos para os apoios.
Passo 6
Para achar o coeficiente de distribuição vamos ter que olhar novamente na tabela de grandezas auxiliares para barras com inércia constante:
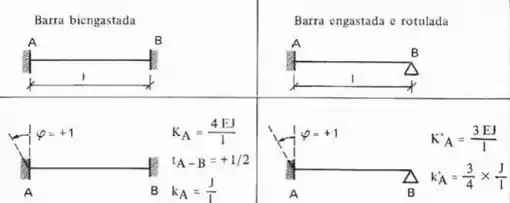
Ta vendo o termo esse é o termo de transmissão e vai valer para vigas biengastadas e será nulo para vigas rotuladas (exatamente porque a rótula permite rotação).
Sendo assim a transmissão para e será igual à metade do valor em :
E será nula para já que é rotulado (coitadinho.. não rotulem seus amigos kkk)
Assim vamos ter:

Esses são os momentos transmitidos maaaasss a gente quer os momentos nos apoios e não os momentos transmitidos de fato. Se lembra que em também exisitia um momento proveniente da carga? Esse momento valia:
Então temos de somar esse momento ao momento transmitido ao ponto :
Assim o resultado final será:
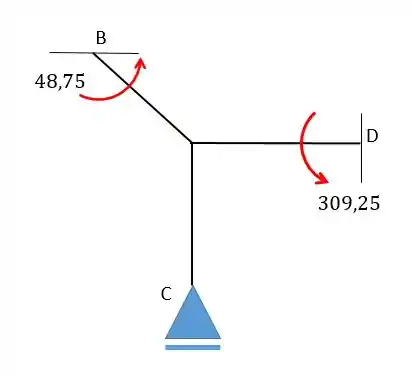
Resposta
