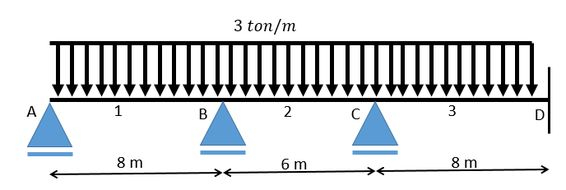
Para o carregamento e a estrutura abaixo encontre os momentos atuantes nos pontos A, B, C e D utilizando o método de Cross. Considere . Obs: Utilize duas casas decimais.
Passo 1
Essa questão pede para acharmos os momentos autantes nas barras, mais precisamente nos pontos dados.
Ao analisar a estrutra nós percebemos que se trata de uma estrutura hiperestática, ou seja, não pode ser resolvida utilizando aquelas equações da estática (somatório das forças e momentos).
Para resolver o exercício pelo método de Cross a gente vai fazer o seguinte passo a passo:
- Substituir os nós por sistemas engastados e com auxílio da tabela de momentos especificar o momento aplicado em cada seção da viga sujeita à carga.
- Calcular os coeficientes de distribuição entorno do nó.
- Aplicar o somatório dos momentos em relação aos pontos “liberando” tais pontos observando que o momento depende de fatores geométricos e dos materiais das barras.
- Calcular os momentos de cada barra segundo os fatores acima apresentados.
Passo 2
A primeira coisa que a gnete faz é a substituição dos nós pelo sistema engastado, como se todas seções da viga estivessm biengastadas mesmo! Para essa representação utilizamos um quadrado, veja:
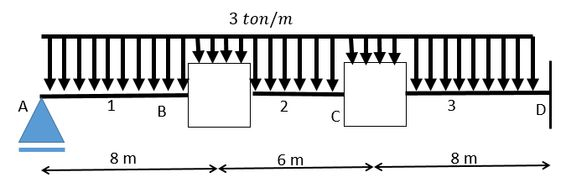
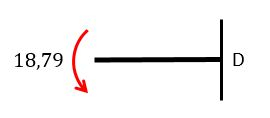
obs: Repare que não é precisa mudar a condição de , isso ocorre simplesmente pelo fato de se localizar na ponta da viga e queremos apenas os momentos internos!
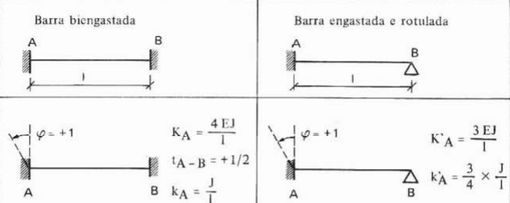
Vamos então olhar na tabela de “Grandezas auxiliares para battas com inércia constante J” e achar o momento. Aqui temos tanto o caso biengastado quanto o caso de um lado engastado e outro rotulado, vamos olhar a tabelinha:
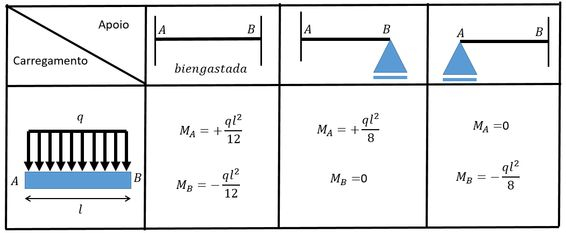
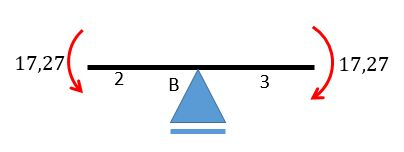
Para a barra 1 temos a terceira condição de contorno (ou bordo) então vamos ter:
Como a carga vale e o comprimento é igual a vamos ter:
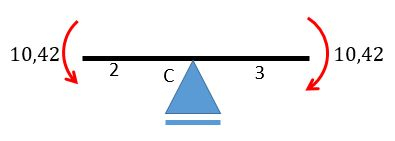
Para a barra 2 vamos ter a primeira condição de contorno, portanto:
Como a carga vale e o comprimento é igual a vamos ter:
Finalmente para a barra 3 também vamos ter a primeira condição de contorno, logo:
Como a carga vale e o comprimento é igual a vamos ter:
Agora a gente pode substituir o carregamento distribuído pelos momentos que calculamos:
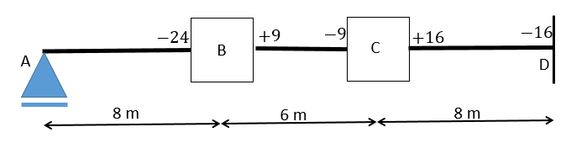
Agora vamos calcular os coeficientes de distribuição.
Passo 3
Os coeficientes de distribuição são os coeficientes que dizem quanto da carga-momento é aplicada em cada barra e são calculados como:
Onde é a rigidez relativa de cada barra. Esse valor da rigidez relativa também é encontrado numa tabela de “Grandezas auxiliares para barras com inércia constante ”. Retirando o caso da viga biengastada da tabela temos:
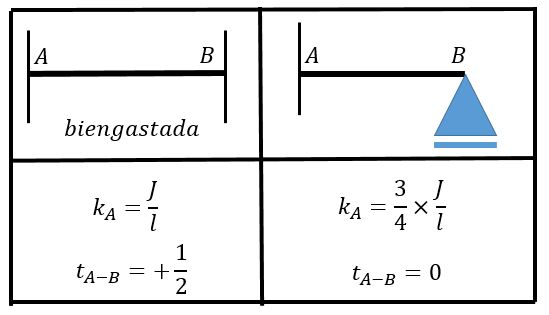
Observe que necessitamos apenas do termo . Agora vamos calcular a rigidez relativa de cada barra. O valor de foi dado no problema e é o comprimento da barra:
Para a barra 1 vamos ter um lado engastado e outro rotulado, então:
Para a barra 2 vamos ter ambos os lados engastados, então:
Para a barra 1 vamos ter ambos os lados engastados, então:
Então como temos todos os agora podemos achar o termo de cada barra. Importando lembrar que isso se refere a cada nó então vamos ter, em torno do nó :
Em torno do nó :
Agora a gente coloca esses dados em conjunto com os momentos calculados no nosso desenho da seguinte forma:
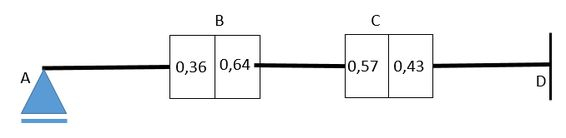
Passo 4
Agora vamos começar o nosso processo iterativo! Diferentemente da primeira questão deste assunto (que tinha apenas um nó) esse problema tem mais de um nó, por isso é necessária a iteração!
O passo zero é colocar os dados de momentos que já calculamos, vai ficar assim:
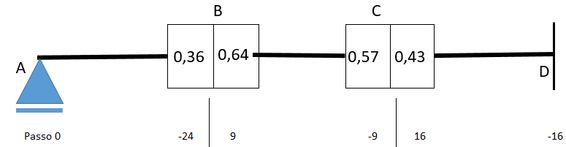
Agora vamos dar o primeiro passo, que consiste em liberar a rotação do nó , desta forma uma carga-momento deverá ser aplicada sobre de forma a permanecer em equilíbrio, o valor dessa carga-momento é igual à diferença entre os momentos de um lado e do outro:
Então é como se a gente tivesse isso aqui:
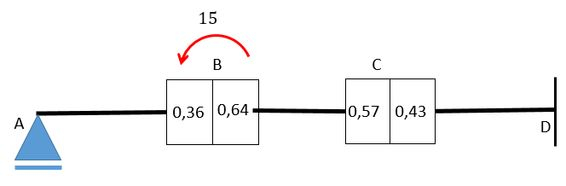
Mas essa carga momento de gera uma momento de igual valor e sentido contrário () que é distribuido para os dois lados do nó pelo coeficiciente de distribuição . E vamos obter:
Pode até reparar que a soma desses momentos é igual a . Então agora vamos obter:
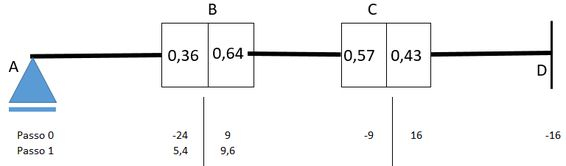
Mas o passo 1 ainda não acabou porque existe ainda o coeficiente de transmissão! O que quer dizer que parte do momento gerado no nó e aplicado a barra 2 (igual a ) irá ser transmitido para o nó pela própria barra 2.
Esse coeficiente de transmissão está explicitado na tabela de grandezas auxiliares para barras com inércia constante e é o termo :
Como temos o caso biengastado ele vale:
Logo a transmissão será igual à metade do valor:
Colocando no nosso diagrama:
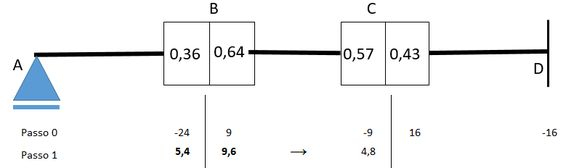
Pronto! O passo 1 está completo e o nosso nó está em equilíbrio por isso marcamos em negrito os valores que obtivemos em vamos fazer isso só para ficar mais evidente, não é super necessário para a resolução da questão.
Observe que, por se tratar de um nó rotulado, nenhum momento é transmitido ao nó .
Passo 5
Agora vamos para o passo 2 que consiste em fazer a mesma coisa que fizemos para o nó mas para o nó que ainda não está em equilíbrio.
Agora vamos liberar e ao fazer isso a carga-momento que aparece será igual à diferença entre os momentos, fazendo o cáclculo vamos obter:
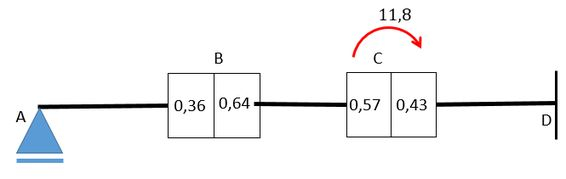
Desta forma os momentos que aparecem no nós devem compensar o momento de logo valerão e terão valor conforme o coeficiente de distribuição desse nó:
Mostrando no desenho
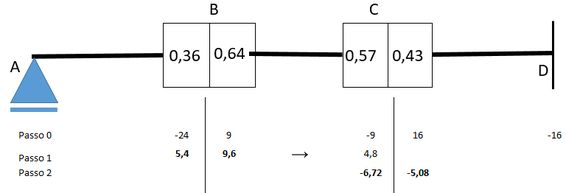
Agora a gente tem que lembrar do coeficiente de transmissão, que vale para ambas as barras 1 e 2 pelo fato das duas estarem biengastadas.
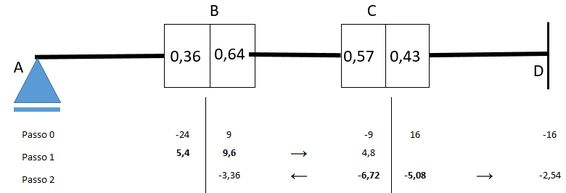
Pronto! Agora temos o ponto em equilíbrio e assim como fizemos no passo anterior marcamos em negrito os valores.
Mas aconteceu uma parada né, o nó recebeu um momento transmitido pela barra 2. Então o nó agora não está mais em equilíbrio.
Por esse motivo vamos voltar ao nó e aplicar os mesmos princípios! Repare que iteração começa a ficar mais evidente e além disso os valores está diminundo, ou seja, convergindo. Graças a deus né!!
Passo 6
Agora a carga-momento aplicado em é igual ao próprio valor recebido pelo nó , portanto, os momentos internos atuantes devem ter valor de para equilibrar e serão distribuídos conforme os coeficientes de distribuição.
Com isso o nosso nó volta ao equilíbrio:
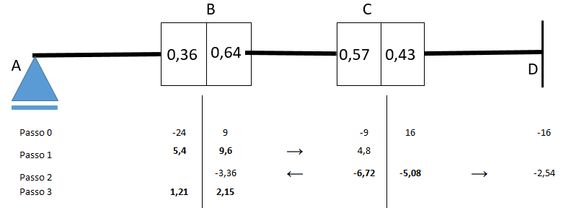
Mas o valor de será transmitido para o nó :
Já reparou no que aconteceu né!!! Já reparou né!!!!
O nó agora saiu do equilíbrio!! PQP que sacoooo....
Isso é chatão eu sei, mas ta indo, acredite!! Tenha MUITA FÉ!
Passo 7
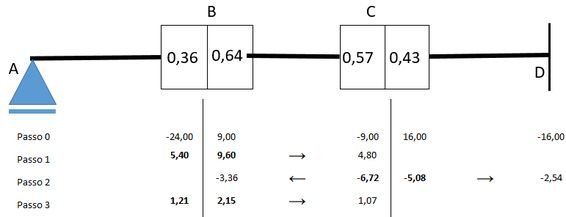
Pessoal agora vamos fazer a mesma coisa, liberar o nó aí vai ter uma carga-momento no valor igual ao transmitido pela barra de e com isso os momentos internos terão de ser iguais a e serão distribuídos conforme os coeficientes de distribuição. NADA DE NOVO NO HORIZONTE, CABRAL!!
obs: Rolou uma aproximação ali, ok? Isso não tem muito problema porque o exercício muitas vezes vai falar para aproximar até a segundo casa decimal, iterar 3 vezes ou coisas desse gênero. Até porque se não houvesse nenhum limite desse tipo iríamos ficar aqui para sempre!
Mostrando na nossa figura:
Esses valores serão transmitidos pelas barras 2 e 3:
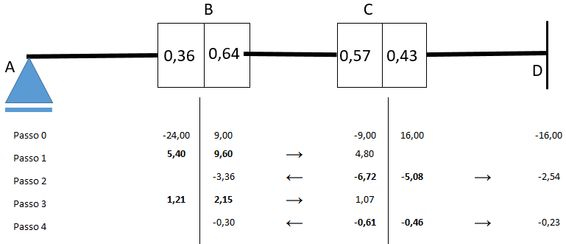
Passo 8
Reparem que o nó não está mais em equilíbrio portanto vamos fazer o mesmo processo novamente. A carga-momento vale , logo o momento interno vale e será distribuído:
No desenho:
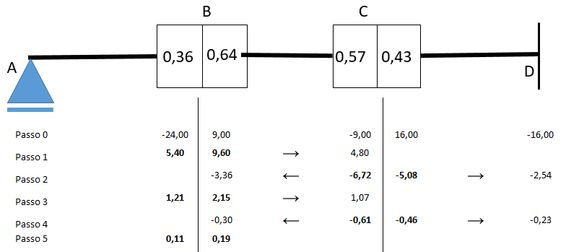
Aplicando a transmissão:
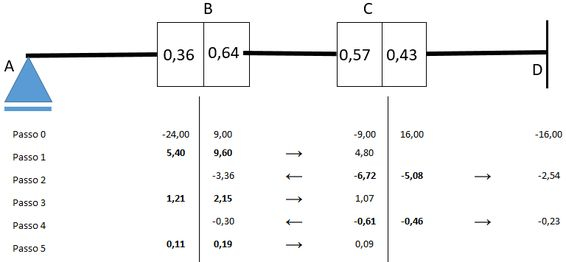
Passo 9
Voltamos para o ponto que terá a carga-momento no valoe de portanto os momentos internos têm valor que serão distribuídos:
No desenho:
Aplicando a transmissão:
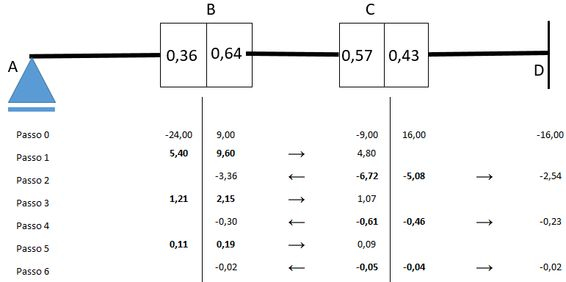
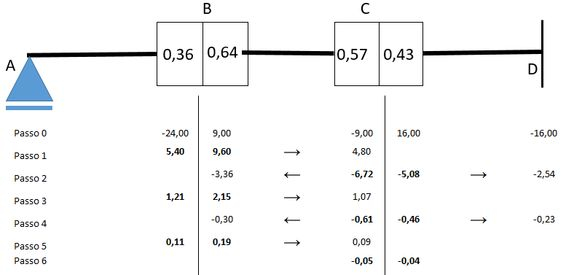
Passo 10
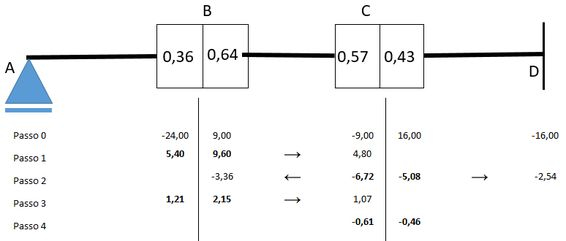
Agora voltando ao ponto nós vamos ter uma carga-momento de portanto os momentos internos são de e vão valer:
Viu como é importante estabelecer um limite de aproximação! A nossa iteração acaba aqui porque houve equilíbrio dos dois lados e vamos representar no desenho como:
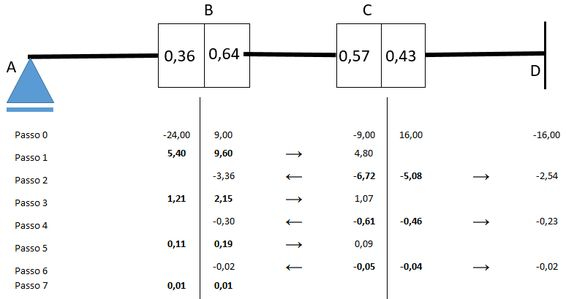
Passo 11
Agora que a nossa iteração acabou, como vamos saber qual o valor do momento de fato?
Agora é só somar todos os termos de cada coluna, fazer a chamada superposição. Assim vamos obter:
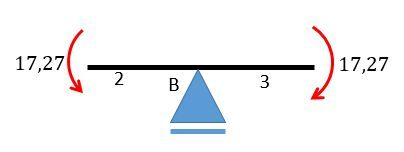
Para o nó , pelo lado esquerdo (referente à barra 1):
Agora pelo lado direito (referente à barra 2):
Viu que o resultado deu igual em módulo e com sentidos opostos? Isso quer dizer que o problema ficou certinho!! Na verdade nem precisamos calcular para ambos os lados, mas fiz isso para mostrar que deu certo!
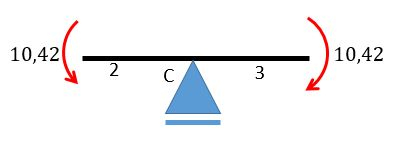
Agora para o nó , pela direita (referente à barra 3):
Finalmente para o nó :
Pessoal lembrem-se que o sentido horário é o positivo hein!!!
Assim vamos ter:
Resposta