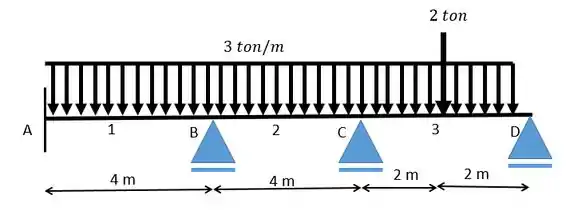
Para a viga e carregamento abaixo e utilizando a tabela fornecida encontre os momentos-carga relativos à carga atuante na viga.
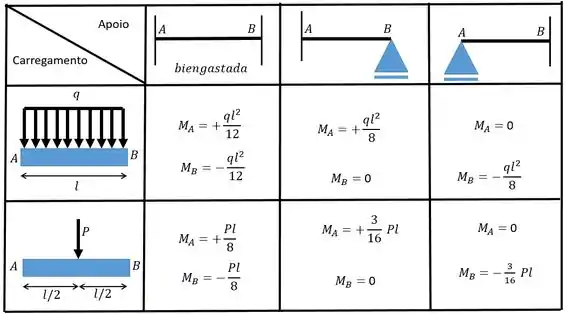
Dado: Tabela de momento de engastamento perfeito.
Passo 1
Na teoria a gente viu que é possível transformar um carregamento em cargas-momento e isso de fato é crucial para qualquer problema deste tipo. E para tal precisamos de auxílio da nossa tabelinha.
Perceba que a tabela fornece 3 situações de apoios e duas situações de carga. Com isso vamos poder achar todos os momentos através das equações mostradas na própria tabela.
Lembre-se que a primeira coisa que devemos fazer é transformar todos os nós internos em nós biengastados.
Passo 2
Primeiro vamos fazer a transformação dos nóis internos apoios biengastados:
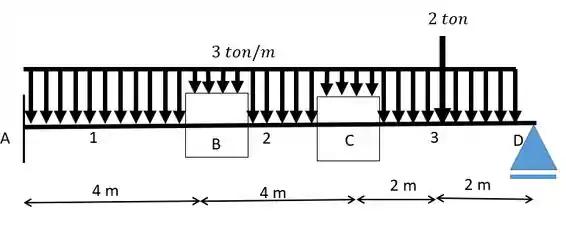
Repare que fizemos isso apenas para os nós internos!
Agora vamos começar pela carga distribuída. Quando temos carga distribuída e viga biengastada vamos ter:
obs: Na tabela aparece e eu coloqueo aqui esquerda e direita para não confundirmos as letras!
obs2: Lembre-se de manter sempre os sinais!! A convenção de sinais é muito importante!
Agora vamos calcular para a barra 1 (caso de distribuição uniforme e apoio biengastado):
Para a barra 2 (também é o mesmo caso de distribuição uniforme e apoio biengastado):
Viu como cada seção da viga aplicada um momento sobre o ponto. Ou seja o mesmo ponto ( poe exemplo) pode estar sujeito a diversos carregamentos!
Passo 3
Vamos para a barra 3 (caso de viga engastada do lado esquerdo e apoiada com rótula do lado direito). Esse caso foi apresentado em outro passo porque agora temos, segundo a tabela:
Olha como o fato de ter uma rótula anula o momento!
Então teremos:
Passo 4
E finalmente temos de calcular o momento relativo à carga pontual. Que é dado por:
Novamente por causa da rótula o momento é nulo.
Vamos ter:
Passo 5
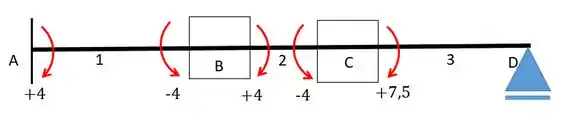
Agora vamos colocar todos esses momentos de volta na nossa figura:

Repare que o momento em relativo à barra 3 é igual a soma dos momentos relativos ao carregamento distribuído com o carregamento pontual
Resposta