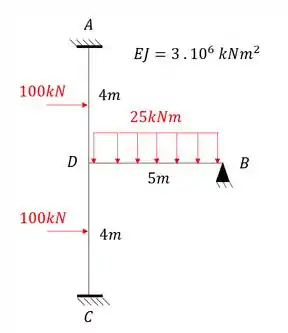
Para estrutura abaixo determine o diagrama de momentos fletores.
Passo 1
Como já sabemos, nossa estrutura apresenta apenas deslocabilidades internas, que são exatamente as deslocabilidades nos nós que não são nem apoio e nem rotulas, sendo assim teremos que a nossa estrutura travada com chapas será:
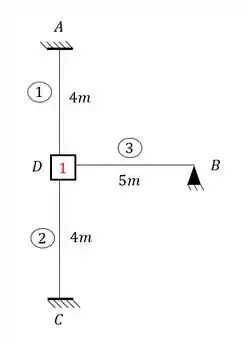
Sabemos que agora temos que determinar as nossas deformações: sendo assim sabemos que:
- Sistema 0
- Sistema 1
- Barra 1 e 2
- Barra 3
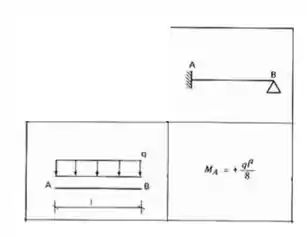
Perceba que para as barras 1 e 2, elas possuem um engaste de um dos seus lados (no ponto A e C) e uma chapa de outro (no ponto D), logo será do tipo Bi-engastada, e a carga nelas é concentrada, sendo assim nossa tabela será:
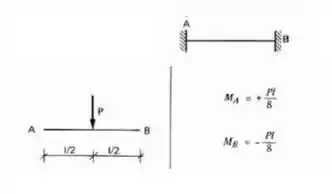
Já para a barra 3, ela possui um apoio de um lado (no ponto B) e uma chapa de outro (no ponto D), logo será do tipo engastado apoiado, e a carga nela é distribuída, sendo assim nossa tabela será:
Calculando na nossa estrutura teremos que:
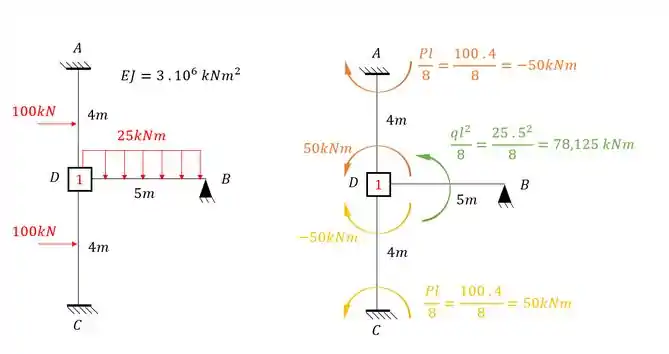
Passo 2
Agora precisamos determinar a parcela referente a rotação que pode ser unitária ou podemos usar o conceito de rigidez relativa:
Sabemos aqui que temos que rotacionar a chapa 1, e sabemos que se fizermos isso nos sentido anti-horário, sempre teremos os nossos momentos positivos, sendo assim teremos a seguinte tabela a ser usada para as barras 1, 2 e 3 respeitando o caso engastado e apoiado e o caso Bi-engastado:
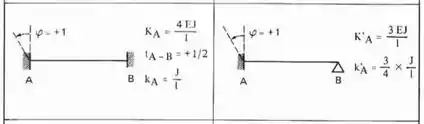
E rotacionando a chapa 1 e aplicando as equações teremos:
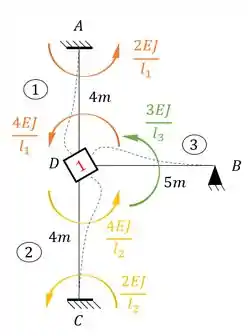
Veja que temos:
Parece meio complicado calcularmos isso, certo? Então podemos usar o nosso fator para rigidez relativa:
E assim teremos:
Substituindo teremos que:
Passo 3
Agora que já fizemos a parte mais difícil, basta montarmos o nosso sistema de equações que será:
Resolvendo esse sistema teremos que:
Para determinação dos momentos fletores, precisamos do momento fletor de todos os nós em todas as barras em todos os sistemas, dessa forma a primeira coisa que devemos fazer é analisar cada sistema.
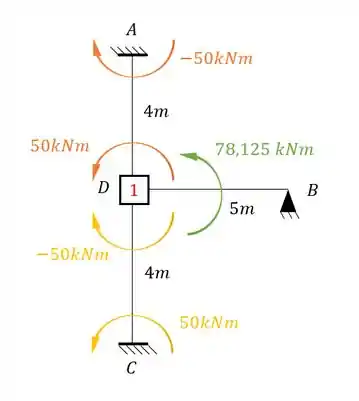
Uma coisa mega importante é lembrar de usar o fator de rigidez relativa EM TODOS OS CASOS que temos para o sistema 1, se não vamos errar, sendo assim teremos que:
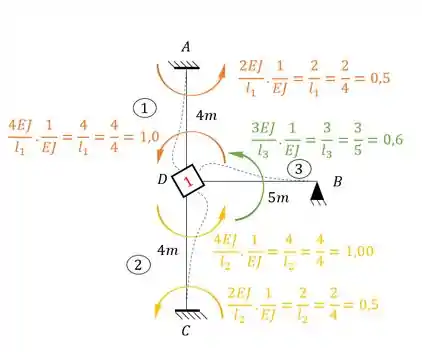
E usando a nossa fórmula para cada nó teremos que:
Vale lembrar que o diagrama de momentos para uma barra com carga distribuída é dado por:
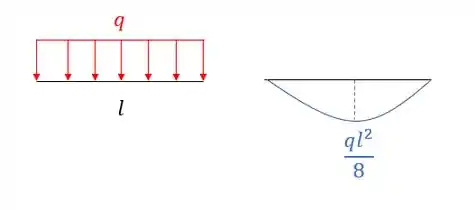
E o diagrama de momentos para uma barra com carga concentrada é dado por:
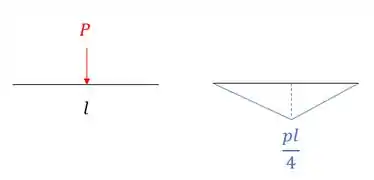
Calculando para cada uma das nossas barras teremos que:
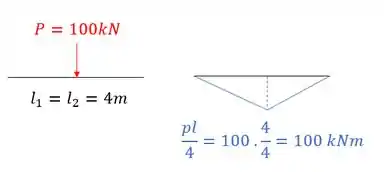
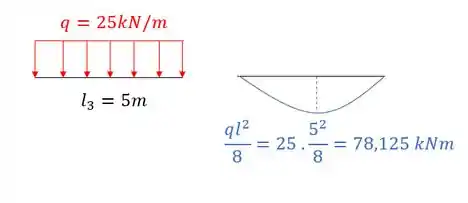
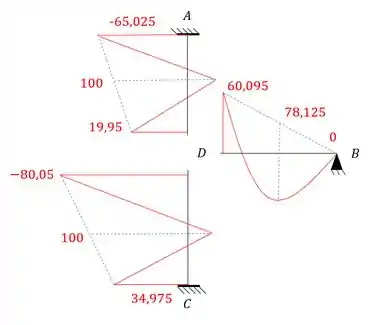
Pode parecer estranho falar disso agora, mas já vai fazer sentido, porque perceba que já temos os momentos de cada nó da nossa estrutura, e para cada barra, sendo assim se desenharmos isso na nossa estrutura teremos que:
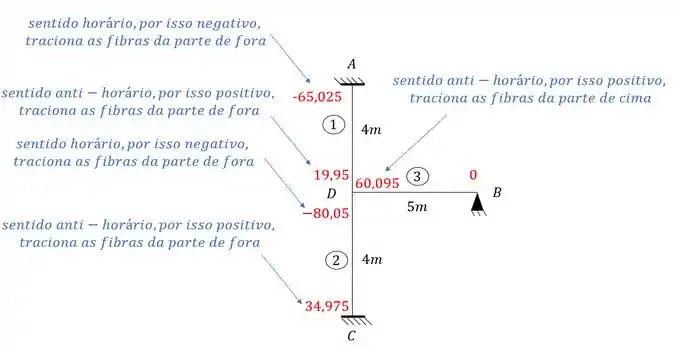
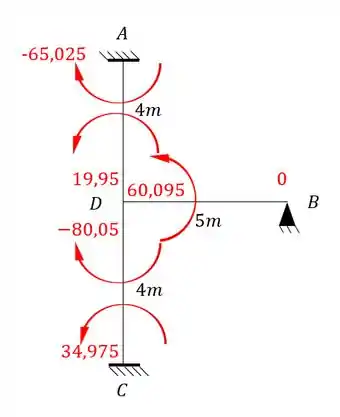
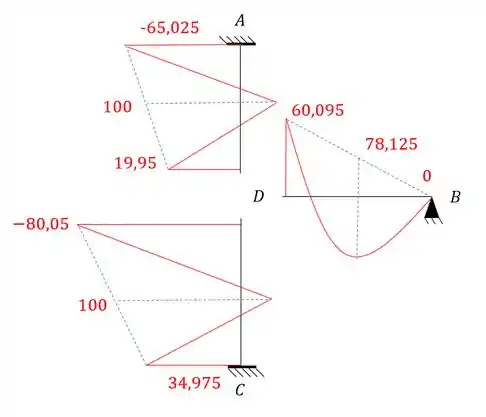
E perceba que o diagrama parabólico (barras 3) e os diagramas triangulares (barras 1 e 2) possuem o momento que calculamos anteriormente pra o meio da viga.
Outra coisa importante é que desenhamos o pórtico separado apenas para facilitar o entendimento do problema.
Resposta