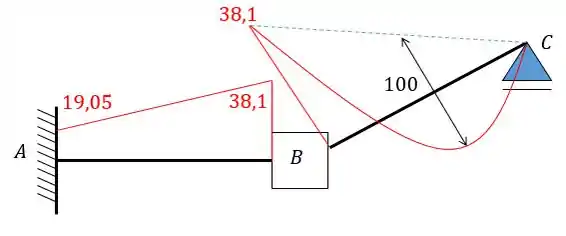
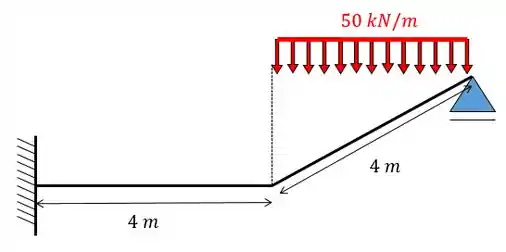
Obter o diagrama de momentos fletores para a viga de inércia constante. Dado: .
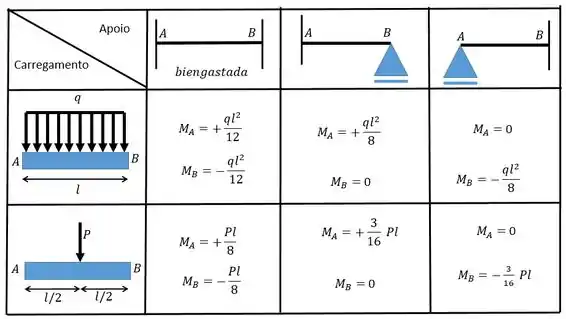
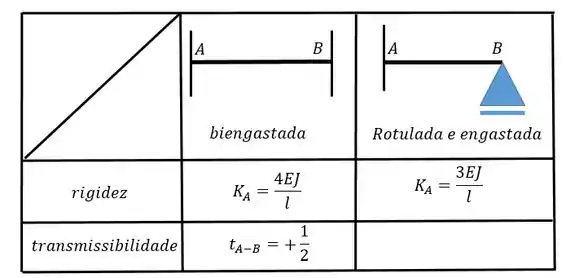
Utilize as seguintes tabelas:
Passo 1
Fala, pessoal!!! A questão pede para que façamos o diagrama dos momentos fletores da nossa viga. Para isso vamos utilizar o método dos deslocamentos. Portanto, vamos seguir o seguinte passo a passo:
- Aplicar o engaste nos nós que possuem deslocabilidades internas.
- Descobrir a equação que rege o sistema.
- Utilizar as tabelas para acharmos os valores de .
- Achar os deslocamentos .
- Com os valores de encontrar os momentos de cada sistema em cada nó.
- Finalmente desenhar o diagrama.
Então partiu!
Passo 2
Como dito a primeiro coisa a se fazer é aplicar o engaste nos nós que possuem deslocabilidades internas, fazendo isso vamos ter:
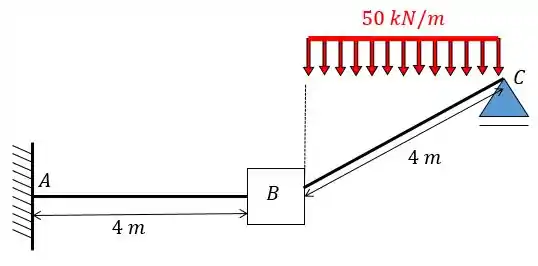
Agora sabemos que temos 1 chapas na nossa estrutura, como podemos ver ali em cima. Como temos apenas uma chapa vamos ter uma equação da forma:
Agora a gente tem que achar os valores de e também!!
Passo 3
Para determinar os valores desses coeficientes nós precisamos combinar o carregamento com a condição dos apoios através da tabelinha:
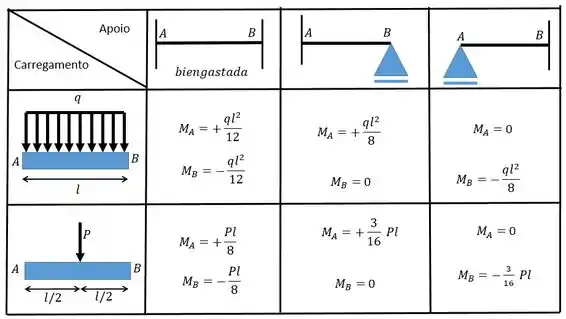
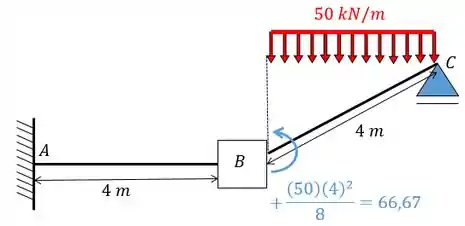
Vamos descobrir primeiro o valor para o sistema 0 que representa o carregamento, neste caso, .
Olhando a conta para cara barra teremos que:
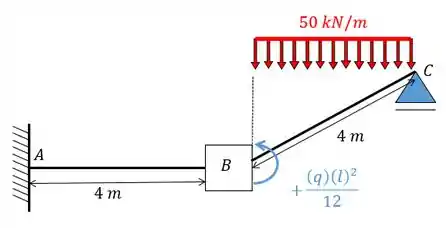
Substituindo os valores vamos ter:
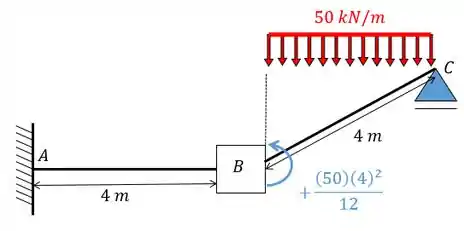
Ou seja, o valor de é:
Passo 4
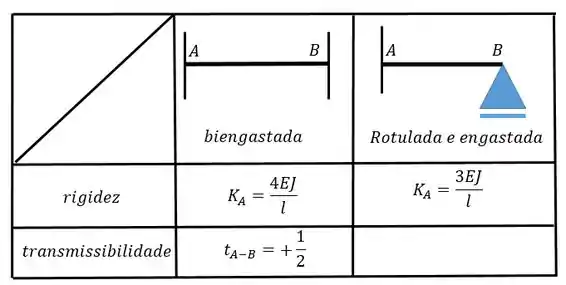
Agora vamos calcular . Para isso vamos precisar da outra tabelinha:
Vamos rotacionar a chapa e obtemos:
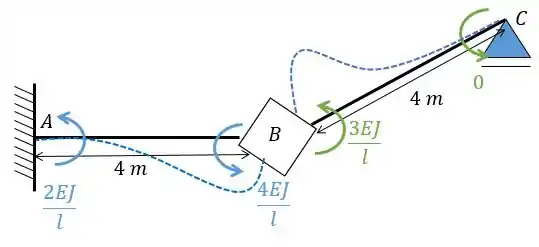
Dessa forma vamos ter:
Como estamos utilizando a rigidez relativa vamos dividir por e obter:
Passo 5
Organizando o sistema temos que:
Substituindo:
E podemos calcular a deformação:
Passo 6
Agora vamos encontrar o momento fletor de cada nó em cada sistema.
- Sistema 0
- Sistema 1
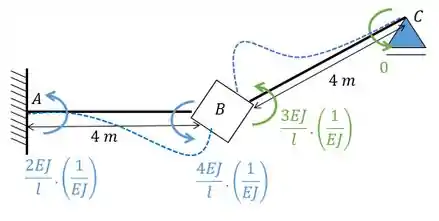
Substituindo os valores vamos ter:
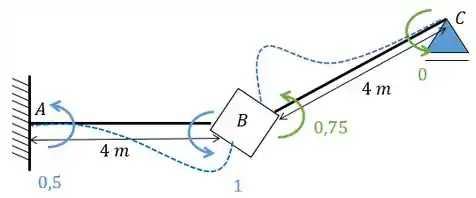
Agora vamos combinar os dois sistemas de forma a obter o momento fletor:
Para a barra vamos ter os nós e , começando pelo nó :
Para o nó nós vamos ter:
Agora para a barra , fazendo primeiro para o nó :
Para o nó :
Passo 7
Colocando os valores que acabamos de achar na viga:
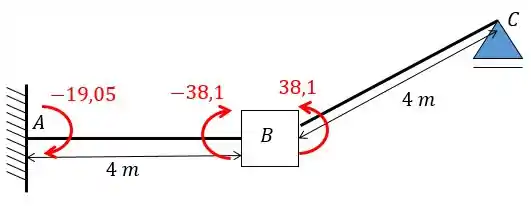
E para acharmos o diagrama a gente precisa lembrar também do diagrama da carga inicial:
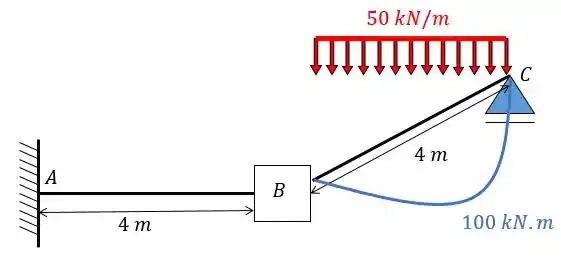
Agora aplicando a combinação das duas vamos ter:
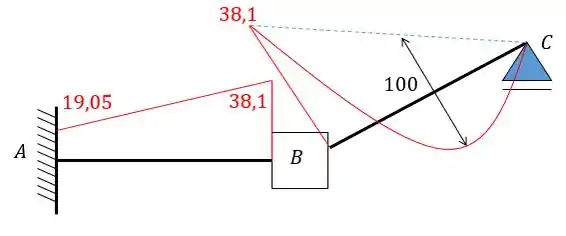
Resposta