Na figura abaixo, temos uma coluna de pratos perfeitos, sem condensador ou refervedor, para separar carga Líquido Saturado com vazão e composição . A carga tem vazão , líquida com . A carga tem vazão , vapor com O topo é com fração molar em . O fundo é com fração molar em .
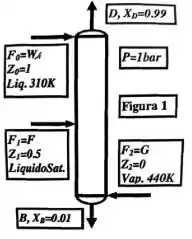
Com balanços materiais e relações Mc-CabeThiele, escreva e as vazões de líquido e vapor das seções (divididas por ) em termos de .
Dados:
Passo 1
Essa questão vai exigir da gente muita manipulação algébrica, e para relacionar as várias relações que ela nos pede vamos precisar começar fazendo um balanço molar.
Como nossa coluna tem três diferentes cargas entrando, vamos adotar a nomenclatura que o enunciado nos forneceu, em que:
Passo 2
O primeiro balanço que vamos fazer vai ser o balanço mássico global. Então, para essa coluna temos:
Dividindo tudo por ,
(1)
Multiplicando por 100 ficamos com:
(2)
Passo 3
Podemos separar a coluna em duas seções, seção de topo em que temos e seção de esgotamento em que temos
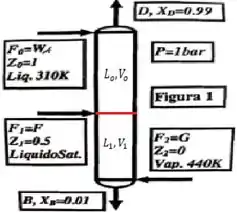
A partir disso, podemos relacionar os valores de fornecido com nossas vazões de líquido e vapor da seguinte forma:
(3)
(4)
(5)
(6)
Passo 4
Agora que temos cinco equações podemos manipular elas. Primeiro, vamos juntas as equações (5) com (6) e dividir por :
(7)
Unindo essa expressão com a expressão (1), ficamos com:
Subtraindo a expressão de cima com , ficamos com:
A partir dessa expressão conseguimos achar a partir de , que é uma das coisas que o enunciado nos pediu.
Passo 5
Já com a expressão de em mãos, conseguimos usar a equação (2) para encontrar :
Com e a equação (7), podemos encontrar também :
Passo 6
E por último, precisamos encontrar , , e . Essa parte já não vamos recorrer tanto ao algebrismo pois basta dividir as equações (3), (4) e (5) por , obtendo:
Repara que na última além de dividir por eu precisei, também, substituir à expressão.