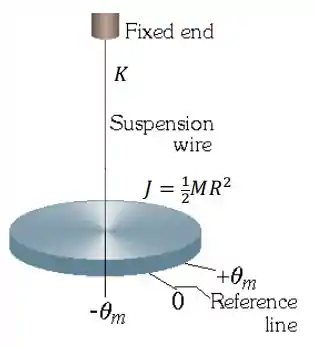
Determine a amplitude e a frequência de oscilação da resposta a um impulso de torque no pêndulo de torção sem atrito representado abaixo, composto de um corpo rígido de inércia rotacional 𝐽 suspenso por um fio com rigidez rotacional 𝐾.
Passo 1
Nesse exercício temos um sistema mecânico rotacional.
Precisamos encontrar uma expressão para o ângulo de rotação , para isso, vmos escrever a equação de equilíbrio de torque:
O torque resultante é a soma de todos os torques, e temos que:
Logo:
Nesse caso, não temos atrito, mas temos um impulso de torque, , e também temos um fio com rigidez rotacional, , que atrapalha a rotação.
Passo 2
Devemos agora aplicar transformada de Laplace na nossa EDO:
Essa parte da transformada de Laplace é bem importante, se você estiver com dúvidas nesse passo seria legal dar uma revisada no tópico de transformadas de Laplace.
A transformada de Laplace da função de torque foi devido ao fato de ser uma função impulso. Funções impulso sempre vão ter transformada de Laplace igual a 1.
Rearranjando:
Passo 3
Já obtivemos a expressão para o ângulo no domínio :
Se manipularmos um pouco teremos:
Fizemod essa manipulação para conseguir aplicar a inversa da transformada de Laplace. Se olharmos uma tabela com transformadas de Laplace, veremos que essa função ficou com o mesmo formato da transformada da função seno. Fazedno a transformada inversa teremos:
Passo 4
O exercício pede a amplitude e frequência de oscilação.
A amplitude é a constante que multiplica a função seno:
E a frequência é o argumento da função: