Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Modelos mecânicos

Ver Teoria
Exercício 51234678

Enunciado

Encontre as função de transferência V 1 s R s para o sistema mecânico abaixo:

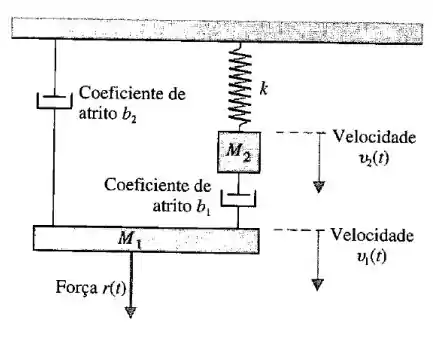
Passo 1

Vamos começar escrevendo a equação de equilíbrio para o bloco 1:

F r = ∑ F

m 1   d 2 x 1 d t 2 = r t - B 2 d x 2 d t - B 1 d x 1 t d t - d x 2 t d t

Como queremos uma expressão que relacione a velocidade com a força r ( t ) :

v t = d x t d t

m 1 d v 1 t d t = r t - B 2 v 1 t - B 1 v 1 t - v 2 t

Rearranjando:

m 1 d v 1 t d t + B 1 + B 2 v 1 t = r t + B 1 v 2 t                           ( 1 )

Analogamente para o segundo bloco teremos:

m 2   d 2 x 2 d t 2 = - k x 2 t - B 1 d x 2 t d t - d x 1 t d t

Fazendo:

v t = d x t d t

E, consequentemente:

x t = ∫ v t d t

m 2 d v 2 t d t = - k ∫ v 2 t d t - B 1 v 2 ( t ) - v 1 ( t )

Rearranjando:

m 2 d v 2 t d t + k ∫ v 2 t d t + B 1 v 2 t = B 1 v 1 t                     ( 2 )

Passo 2

Agora que já fizemos a modelagem do sistema mecânico, devemos aplicar a transformada de Laplace nas expressões (1) e (2).

Para a expressão (1):

m 1 s V 1 s + B 1 + B 2 V 1 s = R s + B 1 V 2 ( s )

Rearranjando:

m 1 s + B 1 + B 2 V 1 s = R s + B 1 V 2 s                           ( 3 )

Aplicando Laplace na expressão (2):

m 2 s V 2 s + k V 2 s s + B 1 V 2 s = B 1 V 1 s                         ( 4 )

Passo 3

Para terminar, vamos isolar V 2 ( s ) em (4) e substituir em (3):

m 2 s + k s + B 1 V 2 s = B 1 V 1 ( s )

V 2 s = B 1 V 1 s   m 2 s + k s + B 1

Substituindo em (3):

m 1 s + B 1 + B 2 V 1 s = R s + B 1 2 V 1 s   m 2 s + k s + B 1          

Logo:

m 1 s + B 1 + B 2 - B 1 2   m 2 s + k s + B 1 V 1 s = R ( s )

m 1 s + B 1 + B 2 m 2 s + k s + B 1 - B 1 2 V 1 s = m 2 s + k s + B 1 R ( s )  

Por fim:

V 1 s R s = m 2 s + k s + B 1 m 1 s + B 1 + B 2 m 2 s + k s + B 1 - B 1 2

Resposta

V 1 s R s = m 2 s + k s + B 1 m 1 s + B 1 + B 2 m 2 s + k s + B 1 - B 1 2