Obtenha a função de transferência, que representa o sistema mecânico abaixo:
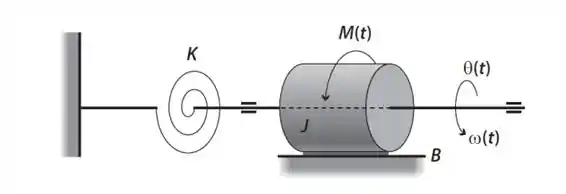
Passo 1
Nesse exercício temos um sistema mecânico rotacional.
O torque resultante é a soma de todos os torques, e temos que:
Logo:
Nesse caso temos um momento angular , mas também temos um momento de atrito e de resistência do fio que “atrapalham” a rotação:
Passo 2
Para achar a função de transferência agora só precisamos aplicar a transformada de Laplace e depois manipular a equação obtida. Aplicando Laplace:
Rarranjando: