Encontre a função de transferência do sistema de massa molo abaixo:
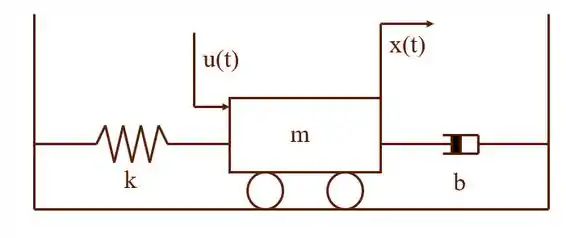
Passo 1
Aqui nessa questão temos um corpor e três forças agindo sobre ele: a força , a força da mola e a força proveniente do sistema de amortecimento. Sendo assim:
Usando a segunda lei de newton:
Sendo a massa do corpo e a aceleração.
Aceleração é a derivada dupla da posição. Substituindo na equação de equilíbrio:
Passo 2
Vamos rearranjar para deixar tudo que tem a a posição do lado esquerdo da equação:
Já temos a nossa EDO no jeitinho. O próximo passo é aplicar a transformada de Laplace nela para que possamos determinar a função de transferência:
Aplicando Laplace:
Só lembrando: se você não está se lembrando como fazer esse passo, seria legal dar uma revisa em transformadas de Laplace. Esse passo é fundamental e precisa estar na ponta da língua hein.
Passo 3
Colocando em evidência do lado esquerdo da equação:
Rearranjando: