Escreva as equações de movimento para a velocidade do carro conforme mostrado na figura abaixo assumindo que o motor fornece uma força . Obetnha a transformada de Laplace da equação diferencial resultante e encontre a função de transferência entre a entrada e a saída .
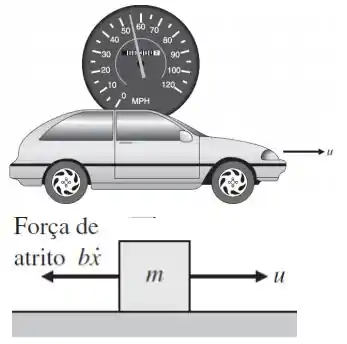
Passo 1
Precisamos encontrar a relação entre a força que o motor aplica no carro e a sua velocidade.
Nesse caso, precisamos considerar duas forças agindo sobre o carro, a força fornececida pelo motor e a força de atrito.
Usando a segunda lei de newton:
Sendo a aceleração do corpo, e aceleração é a derivada dupla da posição. Substituindo na equação de equilíbrio:
Passo 2
Por enquanto, temos uma EDO que relaciona a força fornecida pelo motor com a posição do carro, entretanto, precisamos encontrar a relação com a velocidade e não com a posição. Como a velocidade é a derivada da posição, podemos usar essa relação:
Logo:
Rearranjando:
Passo 3
Obtivemos então a EDO que relaciona a velocidade do carro com a força fornecida pelo motor:
O próximo passo agora é aplicar a transformada de Laplace:
Essa parte da transformada de Laplace é bem importante, se você estiver com dúvidas nesse passo seria legal dar uma revisada no tópico de transformadas de Laplace.
Rearrajando:
Logo: