Encontre as funções de transferência e para o sistema mecânico abaixo:
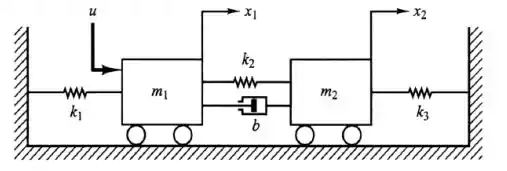
Passo 1
Precisamos então encontrar a função de transferência que relaciona a posição de cada um dos blocos com a força aplicada.
Para o primeiro bloco teremos:
A força resultante ( é igual a soma de todas as forças atuantes no bloco. Para o primeiro bloco temos a força de entrada , a força proveniente das molas 1 e 2 e a força de atrito.
Analogamente para o segundo bloco teremos:
Vamos tentar reorganizar essas equações para conseguir trabalhar com elas um pouco mais facilmente. Para a primeira equação, vamos deixar tudo que tem do lado direito e todo o resto do lado esquerdo:
Para a segunda equação, vamos deixar tudo que tem do lado esquerdo:
Passo 2
Obtivemos então as EDOs que regem o sistema:
O próximo passo agora é aplicar a transformada de Laplace. Para a primeira equação:
E para a segunda:
Rearranjando as equações obtidas:
Passo 3
Para achar as expressões de e precisaremos fazer um pouco de algebrismo. Vamos então isolar na equação (2):
Substituindo na equação (1), teremos:
Rearranjando:
Finalmente:
Já achamos , agora só falta .
Substituindo a equação para que acabamos de encontrar, na equação (2):
Podemos cancelar o termo que aparece dos dois lados da equação:
Finalmente: