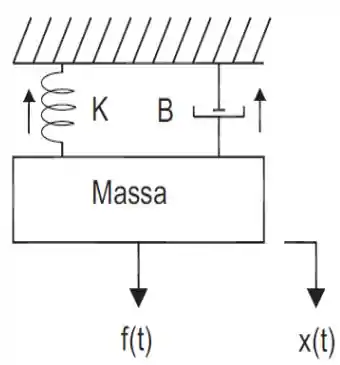
Para o sistema mecânico da figura abaixo, sendo , o sinal de entrada e , o sinal de saída, obter a função de transferência do sistema.
Passo 1
Para esse exercício, precisaremos obter uma relação de equilíbrio entre as diferentes forças envolvidas.
Temos três forças agindo sobre o nosso objeto: a força , a força da mola e a força de atrito.
A força da mola será:
E a força de atrito:
Passo 2
Vamos arbitrar que a força é positiva para baixo e negativa para cima. Sendo assim:
A força resultante sobre o corpo, pode ser escrita usando-se a Segunda Lei de Newton:
Sendo a aceleração do corpor, e aceleração é a derivada dupla da posição. Substituindo na equação de equilíbrio:
Passo 3
Como o exercício pede a função de transferência do sistema, precisamos tirar a transformada de Laplace da equação acima e encontrar a relação entre a força e a posição .
Aplicando Laplace:
Essa parte da transformada de Laplace é bem importante, se você estiver com dúvidas nesse passo seria legal dar uma revisada no tópico de transformadas de Laplace.
Rearrajando:
Logo: