Em um experimento, um laser foi apontado para uma placa, como mostra a figura abaixo:
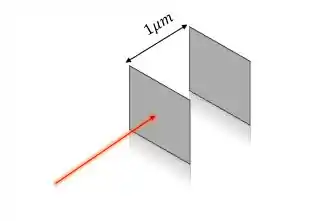
A placa se desloca . Se o laser possui potência de 200W e foi avaliado que o deslocamento durou , calcule:
- A massa da placa
- A densidade de momento linear da placa
Passo 1
Para o item a, vamos começar pelo mais simples, determinando a velocidade:
Para encontrarmos a massa, a gente ainda depende da variação da energia e podemos encontrá-la através da potência:
Passo 2
Agora, podemos usar a conservação de momento linear e encontrar a massa da placa:
Passo 3
Para o item b, a gente vai usar a fórmula da densidade do momento linear:
Como já conseguimos a variação da energia no item anterior e temos a velocidade da luz, agora é só substituir na equação e assim:
Resposta
b)
Exercícios de Livros Relacionados
Em um teste para verificar se a magnetização de um sal paramagnético ao qual se aplica a curva da Fig. 32-14 obedece à lei de Curie, o sal é submetido a uma campo magnético de 0,50T , que permanece co
Um sal paramagnético ao qual a curva de magnetização da Fig. 32-14 se aplica é mantido à temperatura ambiente ( 300K ). Determine para que valor do campo magnético aplicado o grau de saturação magnéti
Uma barra magnética com 6,00c m de comprimento, 3,00m m de raio e uma magnetização uniforme de 2,70 ⋅ 10 3A / m pode girar em torno do centro como uma agulha de bússola. A barra é submetida a um campo
Considere um sólido com N átomos por unidade de volume, cada átomo com um momento dipolar magnético μ → . Suponha que existam apenas duas orientações possíveis para μ → : paralelo ou antiparalelo a um
Um pulso de laser tem energia de 20,0 Je o raio do feixe e de 2,00 mm.A duracao do pulso é 10,0 ns e a densidade de energiae uniformemente distribuida no interior do pulso.(a)Qualéa extensjo espacial