Calcule a circularidade e a esfericidade para um cilindro com altura igual ao dobro do diâmetro da base.
Passo 1
Essa questão é tipo um repeteco da 2, né? Só muda a geometria. Bora dar uma olhada:
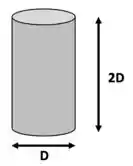
O enunciado pede pra gente calcular a circularidade e a esfericidade dessa partícula. Vamos por partes:
Lembrando a fórmula de circularidade:
Esse * é para lembrar que isso é medido na condição de maior estabilidade da partícula, que, na prática, vai ser pegar o maior perímetro, maior área projetada da partícula. Olha só:
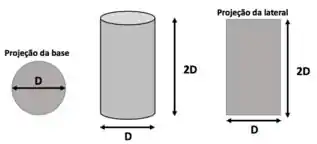
Essa figura tá em escala, daí, nem precisa fazer conta pra ver que a área da projeção lateral é maior do que a da projeção da base. Então, vamos trabalhar com a projeção lateral da partícula no que diz respeito à área e perímetro.
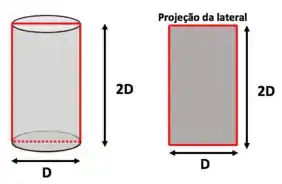
Para o numerador, vamos ter que:
- Calcular a área delimitada por esse retângulo vermelho
- Igualar essa área à fórmula da área do círculo () para achar o diâmetro desse círculo
- Usar esse diâmetro para calcular o perímetro desse círculo, que é o comprimento da circunferência ()
Depois é só calcular o perímetro desse retângulo vermelho e temos o denominador da circularidade também. Aí é só fazer a divisão entre numerador e denominador.
Já para a esfericidade:
Para o numerador, a gente calcula o e usa ele pra calcular a área superficial dessa esfera equivalente (). E pro denominador precisamos da área superficial da partícula em si.
Bora lá que fazendo juntos a gente aprende.
Passo 2
Começando pela circularidade, bora calcular a área projetada na configuração de maior estabilidade da partícula, que é a área daquele retângulo vermelho:
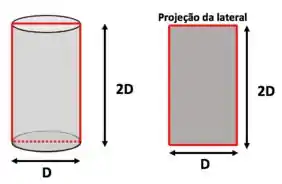
Igualando essa área com a área do círculo:
Usando esse diâmetro para calcular o perímetro desse círculo:
Agora bora calcular o maior perímetro, , da partícula, que é o perímetro daquele retângulo vermelho:
E já que temos numerador e denominador, bora calcular a circularidade:
Passo 3
Hora de calcular a esfericidade:
Já vimos lá no passo 1 que vamos precisar calcular o e, para isso, vamos precisar do volume da partícula, né?
Igualando à fórmula do volume da esfera, para achar o
Aplicando raiz cúbica dos dois lados:
Agora vamos usar esse para calcular a área superficial dessa esfera equivalente (), que vai ser:
Agora precisamos da área superficial da nossa partícula, que vai ser:
Sendo que:
Daí:
Agora é só substituir os valores que achamos na fórmula de esfericidade e ser feliz: