Combustível propano a é misturado continuamente com de excesso de ar a em uma câmara de combustão à pressão atmosférica. Os produtos da combustão saem a , e a vazão volumétrica de ar é de . Determine a taxa de transferência de calor nesse combustor.
Passo 1
Então, galera, esse é um exercício de combustão que pede pra gente calcular a taxa de calor liberada pelo combustível.
Pra calcular , a questão diz que de excesso de ar é consumido na combustão. Isso significa que foi utilizado de ar teórico na combustão.
Relaxa que a importância dessa porcentagem de ar teórico vai ficar mais clara mais pra frente.
Para achar , temos que usar a primeira lei da termodinâmica adaptada à combustão. Essa fórmula se encontra abaixo.
O somatório da esquerda é a soma das entalpias dos reagentes que são queimados a cada segundo e o somatório da direita é a soma das entalpias dos produtos que são gerados a cada segundo. é a taxa de trabalho realizada. Ela vale zero, porque o enunciado só diz que calor é trocado. Ele não cita nenhum trabalho sendo realizado nessa combustão.
Pra achar vamos ter que encontrar o valor desses dois somatórios. Mas para encontrar os somatórios, vamos precisar calcular as vazões molares presentes nesses somatórios. Então vamos começar as contas tentando encontrar as vazões molares.
Passo 2
Começamos a calcular as vazões molares, escrevendo a equação química da combustão.
O enunciado diz que a combustão teve muito excesso de ar. Logo, a combustão foi completa e gerou , , e como produto. Como o ar é composto por e , o , o e o são os reagentes.
onde , , , , e são os coeficientes estequiométricos da combustão.
Esses coeficientes são iguais às vazões molares! Por exemplo, o coeficiente do combustível é igual à vazão molar desse combustível .
Isso quer dizer que achar as vazões molares é a mesma coisa que achar os coeficientes.
No entanto, para encontrar a vazão molar , temos que encontrar a vazão molar de ar primeiro.
Achamos usando a equação P-V-T de gases perfeitos mostrada abaixo.
onde é a pressão do ar que é igual à pressão atmosférica segundo o enunciado. Logo, vale:
é a constante universal dos gases. Ela vale . é a temperatura do ar em kelvin . Logo, temos que converter a temperatura de pra , somando à temperatura.
é a vazão volumétrica de ar que vale segundo o enunciado.
Repare que essa equação P-V-T de gases perfeitos usa a vazão volumétrica do gás ao invés de usar o volume do gás. Nós fazemos essa mudança, quando queremos calcular a vazão molar do gás ao invés de calcular a quantidade de mol do gás! Substituindo os dados:
No próximo passo, nós vamos aprender a achar a vazão molar de combustível a partir da vazão molar de ar .
Passo 3
Com a vazão molar de ar somos capazes de ar o coeficiente .
Como o ar é formado por e , a vazão molar de ar é a soma entre a vazão molar de e a vazão molar de . Logo:
Substituindo o valor de , achamos o valor de .
Esse coeficiente é a vazão molar de ! Além disso, achar o coeficiente é fundamental pra achar a vazão molar do combustível! Veremos agora o motivo!

Quando a questão diz que o combustível é queimado completamente com de ar teórico, ela quer dizer que a vazão molar de é vezes maior que a vazão que o teria caso a combustão não tivesse excesso de ar.
Agora, pra achar o coeficiente , temos que equilibrar a equação de combustão sem excesso de ar de .
Ou seja, precisamos achar o valor do coeficiente para o caso da combustão ser completa sem a geração de nos produtos, como mostrado abaixo.
onde , , , e são os coeficientes estequiométricos da combustão sem excesso de ar.
Para encontrar , devemos encontrar antes e . O coeficiente é encontrado através do balanço de carbono . Para a quantidade de ficar balanceada, os de dos reagentes e os de dos produtos devem ser iguais.
Já o coeficiente é determinado por meio do balanço do hidrogênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Por fim, achamos o coeficiente , fazendo o balanço de oxigênio . Os de dos reagentes têm que ser iguais aos de dos produtos.
Substituindo o valor de :
Pronto, achamos o coeficiente !
Para achar os outros coeficientes da combustão com excesso de ar, vamos fazer o balanço da equação de reação no próximo passo.
Passo 4
Os coeficientes restantes da combustão com excesso de ar são encontrados através do balanço da equação abaixo.
Calculamos o coeficiente através do balanço de carbono . Para ficar balanceado, os de dos reagentes devem ser iguais aos de dos produtos.
é calculado pelo balanço do hidrogênio . Os de dos reagentes precisam ser iguais aos de dos produtos.
Calculamos por meio do balanço do oxigênio . Esse balanço faz com que os de dos reagentes sejam iguais aos de dos produtos.
Por fim, encontramos pelo balanço de nitrogênio ! Os de dos reagentes são iguais aos de dos produtos.
A vazão molar de dos reagentes é igual à , a vazão molar de dos reagentes e dos produtos é igual a , a vazão molar de é igual à , a vazão molar de é igual à e a vazão molar do dos produtos é igual a .
Pronto! Achamos as vazões molares. No entanto, ainda precisamos encontrar as entalpias de formação e as diferenças de entalpia pra achar os somatórios!
Passo 5
As entalpias de formação de e valem zero porque os dois são substâncias quimicamente mais estáveis.
As entalpias de formação de , e são encontradas em tabelas, como a tabela abaixo. Mas tome cuidado! Precisamos pegar o valor da entalpia de formação de vapor de , porque os produtos de combustão estão muito quentes (estão a ).
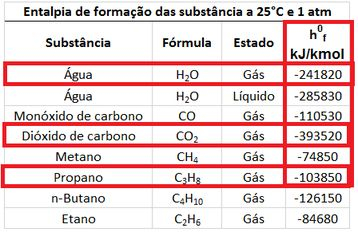
Eba! Estamos quase com todos os valores que precisamos. Só falta achar as diferenças de entalpia nos passos seguintes!
Passo 6
é a diferença entre a entalpia de uma substância a temperatura e a entalpia de uma substância a temperatura de . Como o enunciado diz que está a , o de vale zero.
Pra encontrar o dos reagentes que restam, temos que converter a temperatura desses reagentes de pra . Fazemos isso, somando à temperatura!
Os valores de para os produtos são determinados por tabelas. Nem sempre temos a disposição tabelas com valores de . As vezes, as tabelas mostram o valor da entalpia na temperatura de e o valor da entalpia na outra temperatura de e nós temos que calcular subtraindo esses dois valores.
Então, vamos resolver esse exercício como se a gente só tivesse esse tipo de tabela a disposição! Repare que as tabelas que usaremos não têm os valores de entalpia para a temperatura de . Ou seja, precisaremos interpolar as tabelas pra achar !
Vamos iniciar achando de dos reagentes.
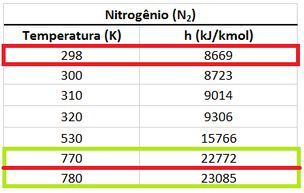
de dos reagentes vale:
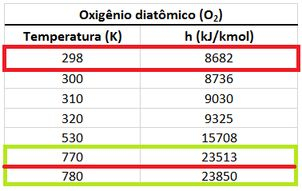
No próximo passo nós vamos descobrir os valores de dos produtos!
Passo 7
Pra encontrar o dos produtos, temos que converter a temperatura desses produtos de pra . Fazemos isso, somando à temperatura!
Os valores de para os produtos são determinados por tabelas. Nem sempre temos a disposição tabelas com valores de . As vezes, as tabelas mostram o valor da entalpia na temperatura de e o valor da entalpia na outra temperatura de e nós temos que calcular subtraindo esses dois valores.
Preste atenção! As tabelas que usaremos também não têm os valores de entalpia para a temperatura de . Ou seja, precisaremos interpolar de novo as tabelas pra achar !
Vamos iniciar achando de dos produtos.
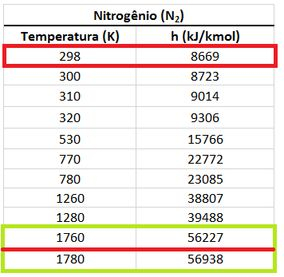
de dos produtos vale:
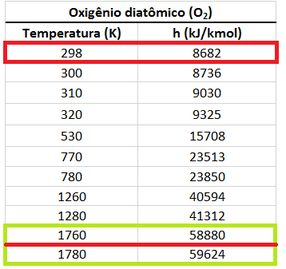
de dos produtos vale:
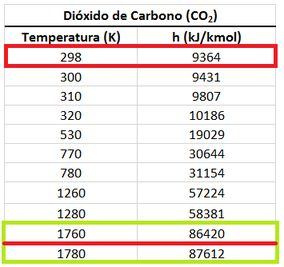
de dos produtos vale:
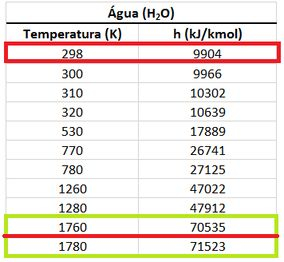
Com esses valores podemos achar os somatórios na próxima etapa!
Passo 8
Como foi dito antes, o somatório da esquerda é a soma das entalpias dos reagentes que são queimados a cada segundo. Isso quer dizer que esse somatório é igual às entalpias específicas dos reagentes multiplicadas pelas vazões molares dos reagentes!
Calculando separadamente cada termo da soma:
Juntando os termos novamente, chegamos no valor do somatório da esquerda.
Agora, vamos partir pro cálculo do somatório da direita. Conforme já foi dito antes, o somatório da direita é a soma das entalpias dos produtos que são queimados a cada segundo. Isso quer dizer que esse somatório é igual às entalpias específicas dos produtos multiplicadas pelas vazões molares dos produtos!
Calculando separadamente cada termo da soma:
Juntando os termos novamente, chegamos no valor do somatório da direita.
Substituindo os somatórios na primeira lei, encontramos:
Menin@ do céu! Quanto trabalho!
Pois é.... exercícios de primeira lei da combustão são mais demoradinhos mesmo. Mas esses são os exercícios que podem cair na sua prova. Então vale muito a pena fazer!