Análise de Eventos a partir de Conjuntos
Produzido por Jorge Alberto NascimentoTeoria
Agora que você já conseguiu entender bem a diferença entre espaço amostral e evento, vamos falar de uma coisa BEM importante. Lembra que no tópico passado acabamos definindo o espaço amostral como a união de vários eventos?
Então, união é utilizada na Teoria dos Conjuntos. Na realidade ela é uma das operações que utilizamos para relacionar conjuntos. E o que isso tem a ver com probabilidade? Eeeesse que é o ponto: podemos fazer uma analogia com conjuntos SEMPRE. E isso é um bizu.
É um bizu pois isso facilita na hora de interpretar um problema, de visualizar. Vamos entender como...
Imagina que fizemos uma pesquisa na faculdade, cuja pergunta era: Você considera o brownie a melhor sobremesa?
Temos que:
Espaço amostral: Todos os alunos da faculdade.
Evento A: Pessoas que consideram brownie a melhor sobremesa.
Evento B: Pessoas que não consideram brownie a melhor sobremesa.
Perceba que quem não está no evento A está necessariamente no evento B e vice-versa. Quando isso acontece, dizemos que o evento B é o complementar de A . Desenhando seria:
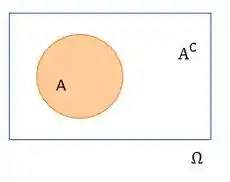
Agora imagina se mudássemos a pergunta para: O que você prefere como sobremesa: brownie ou palha italiana?
Temos que:
Espaço Amostral: Todos os alunos da faculdade
Evento A: Pessoas que preferem o brownie
Evento B: Pessoas que preferem a palha italiana
Além disso, neste caso teremos mais dois eventos:
Evento C: Pessoas que gostam tanto de palha quanto de brownie
Evento D: Pessoas que não gostam de nenhum dos dois.
E agora? Vamos olhar para os conjuntos:
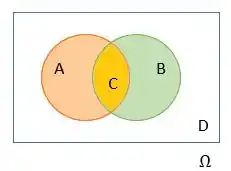
Análise de Conjuntos
1º - Vamos olhar para todas as pessoas que responderam sim para a enquete, seja para a palha italiana, quanto para o brownie. Olhando para elas, estou olhando para a união dos conjuntos A e B (, ou seja, para a união do grupo de pessoas que prefere palha e do grupo que prefere brownie. Ali tem pessoas que só comem brownie, só comem palha... e que comem ambos!
A união é isso!
União ocorre quando pelo menos um dos eventos, ou , ocorrer.
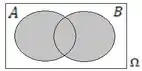
2º - Esse evento C, concordam que é a interseção do evento A com o evento B?
Opa, não lembra o que é interseção?
Interseção ocorre quando e ocorrem simultaneamente.
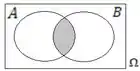
São as pessoas que gostam tanto de brownie quanto de palha italiana. Elas estão ali dentro da união dos conjuntos, mas são mega especiais pois gostam dos dois.
MAS e se não tiver ninguém que goste dos dois?
Nesse caso chamamos essse conjunto de mutuamente exclusivos, ou disjuntos. Essas palavrinhas só significam que . Nesse caso teremos que:
3º - E o evento D, concordam que são as pessoas que não estão nem no evento A nem no evento B? Ou seja, que não gostam de nenhum dos dois?
Ou seja, se eu olhasse para o conjunto como se ele fosse um big conjunto, poderíamos dizer que o evento D é o complementar desse conjunto? Sim!
Importante
Apesar do exemplo ser com apenas dois conjuntos, essas propriedades valem para mais.
No caso de três conjuntos, podemos dizer que:
Análise de Conjuntos
Exercícios Resolvidos
Exercício Resolvido #1
PUCRIO-P1-2012.1-1B
b) Defina formalmente uma partição de um espaço amostral. Use o diagrama de Venn para ilustrar.
Passo 1
Vamos supor um espaço amostral, .
Vamos dizer também que temos vários eventos: .
Dizemos que esses eventos formam uma partição do nosso espaço amostral, se:
- Todos tiverem probabilidade de acontecer maior que 0:
- Eles forem mutuamente exclusivos, ou seja, a interseção de qualquer um deles ser nula:
- A união de todos eles formar o nosso espaço amostral:
Passo 2
Usando o diagrama, teríamos algo assim:
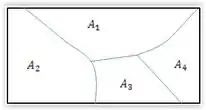
Em poucas palavras, partição de um espaço amostral, são vários eventos mutuamente exclusivos cuja união forma o espaço amostral.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 110-12
Considere o lançamento de dois dados. Considere os eventos: A= soma dos números obtidos igual a 9 e B = número no primeiro dado maior ou igual a 4. Enumere os elementos de A e B. Obtenha , e .
Passo 1
Primeiramente vamos escrever o espaço amostral:
Seja (i,j) o resultado em i do dado 1 e de j do dado 2.
{(1,1); (1,2);(1,3);(1,4);(1,5);(1,6);(2,1); (2,2);(2,3);(2,4);(2,5);(2,6);(3,1);(3,2);(3,3);(3,4);(3,5);(3,6);(4,1);(4,2);(4,3);(4,4);(4,5);(4,6);(5,1);(5,2);(5,3);(5,4);(5,5);(5,6);(6,1);(6,2);(6,3);(6,4);(6,5);(6,6)}
Passo 2
Seja o evento A igual a soma dos números obtidos igual a 9.
A= {(3,6);(4,5);(5,4);(6,3)}
Passo 3
Seja o evento B igual a todas as combinações cujo o número no primeiro dado seja maior ou igual a 4.
B = {(4,1);(4,2);(4,3);(4,4);(4,5);(4,6);(5,1);(5,2);(5,3);(5,4);(5,5);(5,6);(6,1);(6,2);(6,3);(6,4);(6,5);(6,6)}
Passo 4
Agora que já sabemos quem são os conjuntos, vamos calcular:
(i) ,
(ii)
(iii) .
Passo 5
Calculando (i) :
A= {(3,6);(4,5);(5,4);(6,3)}
B = {(4,1);(4,2);(4,3);(4,4);(4,5);(4,6);(5,1);(5,2);(5,3);(5,4);(5,5);(5,6);(6,1);(6,2);(6,3);(6,4);(6,5);(6,6)}
= {(3,6);(4,1);(4,2);(4,3);(4,4);(4,5);(4,6);(5,1);(5,2);(5,3);(5,4);(5,5);(5,6);(6,1);(6,2);(6,3);(6,4);(6,5);(6,6)}
Basta unir os conjuntos, ou seja, os elementos que forem diferentes devem ser adicionados e os repetidos só devem ser contados uma única vez.
Passo 6
Calculando (ii)
A= {(3,6);(4,5);(5,4);(6,3)}
B = {(4,1);(4,2);(4,3);(4,4);(4,5);(4,6);(5,1);(5,2);(5,3);(5,4);(5,5);(5,6);(6,1);(6,2);(6,3);(6,4);(6,5);(6,6)}
= {(4,5);(5,4);(6,3)}
Para calcular a interseção basta verificar quais elementos são comuns aos dois eventos.
Passo 7
Calculando (iii) .
A= {(3,6);(4,5);(5,4);(6,3)}
{(1,1); (1,2);(1,3);(1,4);(1,5);(1,6);(2,1); (2,2);(2,3);(2,4);(2,5);(2,6);(3,1);(3,2);(3,3);(3,4);(3,5);(3,6);(4,1);(4,2);(4,3);(4,4);(4,5);(4,6);(5,1);(5,2);(5,3);(5,4);(5,5);(5,6);(6,1);(6,2);(6,3);(6,4);(6,5);(6,6)}
= {(1,1); (1,2);(1,3);(1,4);(1,5);(1,6);(2,1); (2,2);(2,3);(2,4);(2,5);(2,6);(3,1);(3,2);(3,3);(3,4);(3,5);(4,1);(4,2);(4,3);(4,4);(4,6);(5,1);(5,2);(5,3);(5,5);(5,6);(6,1);(6,2);(6,4);(6,5);(6,6)}
Resposta
A= {(3,6);(4,5);(5,4);(6,3)}
B = {(4,1);(4,2);(4,3);(4,4);(4,5);(4,6);(5,1);(5,2);(5,3);(5,4);(5,5);(5,6);(6,1);(6,2);(6,3);(6,4);(6,5);(6,6)}
= {(3,6);(4,1);(4,2);(4,3);(4,4);(4,5);(4,6);(5,1);(5,2);(5,3);(5,4);(5,5);(5,6);(6,1);(6,2);(6,3);(6,4);(6,5);(6,6)}
= {(4,5);(5,4);(6,3)}
{(1,1); (1,2);(1,3);(1,4);(1,5);(1,6);(2,1); (2,2);(2,3);(2,4);(2,5);(2,6);(3,1);(3,2);(3,3);(3,4);(3,5);(4,1);(4,2);(4,3);(4,4);(4,6);(5,1);(5,2);(5,3);(5,5);(5,6);(6,1);(6,2);(6,4);(6,5);(6,6)}
Exercício Resolvido #3
Marcos Nascimento Magalhães e Antonio Carlos Pedroso de Lima, Noções de Probabilidade e Estatística, 6ª ed. São Paulo: Edusp, 2004, 41-02
Sendo A e B dois eventos em um mesmo espaço amostral, “traduza” para a linguagem da Teoria dos Conjuntos, as seguintes situações:
a) Pelo menos um dos eventos ocorre.
b) O evento A ocorre mas B não.
c) Nenhum deles ocorre.
Passo 1
Vamos lá: A e B são eventos ou seja, subconjuntos do meu espaço amostral.
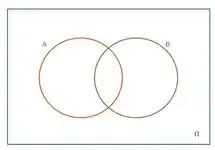
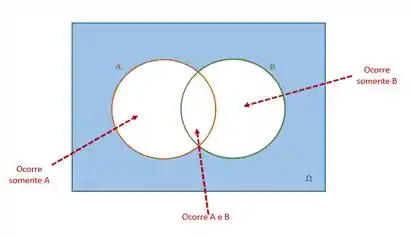
Como o enunciado não informou se eles possuem interseção ou não, vamos considerar que tem. (Note que não tem problema considerar que , pois este é o caso mais abrangente.)O diagrama de Venn ficaria assim:
Passo 2
a) Pelo menos um evento ocorre.
Vamos interpretar essa frase: Se pelo menos um evento ocorre podemos dizer que ou apenas UM evento ocorre (ou A ou B) ou AMBOS ocorrem. Olhe na figura abaixo:
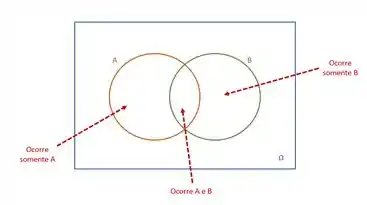
Note que a união desses três subconjuntos é exatamente .
Obs.: É bem comum, ao ler o “pelo menos um evento ocorre” pensar no espaço amostral (conjunto universo) menos o contrário do enunciado. Como assim?
Ele não pediu pelo menos um dos eventos ocorra? O contrário disso, o complementar, é que nenhum evento ocorra concordam?
Escrevendo “nenhum evento ocorra”:
Então escreveríamos:
Passo 3
b) O evento A ocorre mas B não.
Se o evento A ocorre mas o B não, podemos afirmar que neste caso a interseção de A com B (não irá ocorrer.
Na figura, a área preenchida será a desejada:
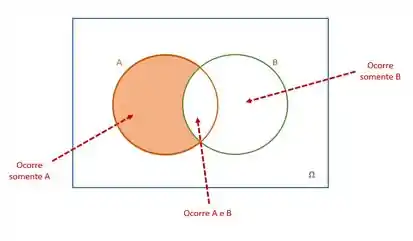
Essa área pode ser escrita como: ou .
Passo 4
c) Nenhum deles ocorre.
Se nenhum deles ocorre, note que teremos exatamente o oposto da letra (a), ou seja, o complementar da mesma.
Assim, nenhum deles ocorre quando em .
Resposta
a) ou
ou
c)
Exercício Resolvido #4
Marcos Nascimento Magalhães e Antonio Carlos Pedroso de Lima, Noções de Probabilidade e Estatística, 6ª ed. São Paulo: Edusp, 2004, 50-06
Para dois eventos A e B, num mesmo espaço amostral, verifique, através de um diagrama, que é sempre possível escrever o evento A como sendo e que, portanto, vale .
Passo 1
Primeiro, antes de qualquer coisa vamos desenhar o nosso espaço amostral e seus respectivos subconjuntos (eventos).
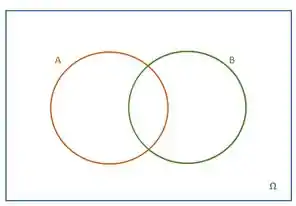
Feito isso, vamos começar a analisar a expressão dada:
A melhor idéia aqui é analisar por partes. Vamos dividir?
(i)
(ii)
Passo 2
Analisando (i) :
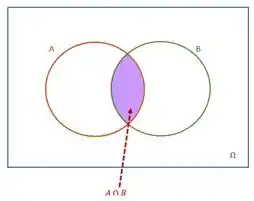
Passo 3
Analisando (ii)
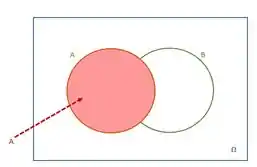
A
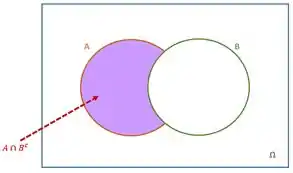
Passo 4
Fazendo
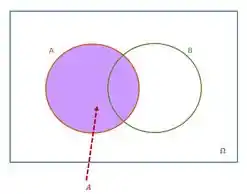
Ou seja, através do diagrama verificamos que A= .
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Elaboração própria
Em uma pesquisa de mercado foram entrevistadas várias pessoas acerca de suas preferências em relação a dois produtos, A e B. Os resultados da pesquisa indicaram que:
- 180 pessoas compraram o produto A
- 200 pessoas compraram o produto B
- 30 pessoas compraram os dois produtos
- 80 pessoas não compraram nenhum dos dois produtos
Quantas pessoas foram entrevistadas?
Passo 1
Vaamos lá!
Esse é um problema clássico que envolve conjuntos. Temos dois conjuntos, que possuem (ou não) interseção.
O primeiro passo é desenha-los e entender bem o que cada região significa.
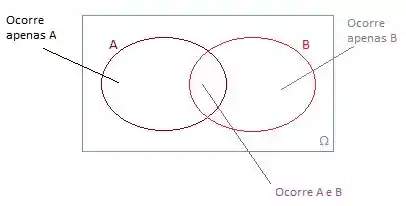
Passo 2
Agora que cada região está bem definida, vamos começar a completar o conjunto com os dados do enunciado. Existe uma ordem que é melhor para completar e torna todo o processo mais fácil.
1º - Completar a região da interseção dos dois conjuntos/eventos.
“30 pessoas compraram os dois produtos”
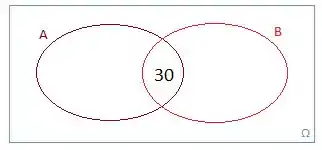
2º - Completar as regiões que representam as pessoas que compraram apenas UM produto. Ou seja, compraram ou A, ou B.
Devemos tomar cuidado pois o valor do enunciado não será o mesmo que escreveremos nessas regiões. Devemos subtrair do valor já existente na interseção dos dois.
Vamos pro diagrama!
“180 pessoas compraram o produto A”
“200 pessoas compraram o produto B”
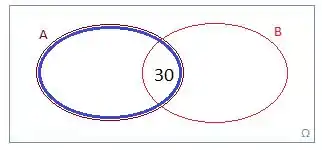
Toda essa região que eu marquei de azul representa as pessoas que compraram o produto A, certo?
Aquele 30 ali, apesar de estar na interseção, também representa pessoas que compram o produto A!
Ou seja, se 180 pessoas compraram o produto A, o valor que temos que completar ali é .
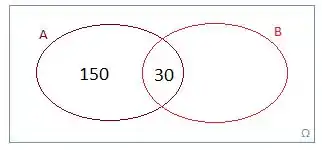
Agora seguindo o mesmo raciocínio, vamos completar as pessoas que compram o produto B!
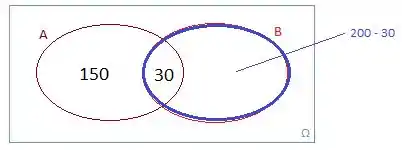
Logo, teremos pessoas que compram o produto B!
Ficamos assim, então:
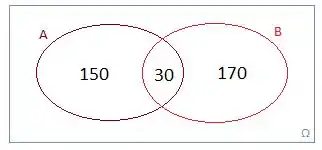
3º - Completar com os elementos que não pertecem a nenhum desses conjuntos.
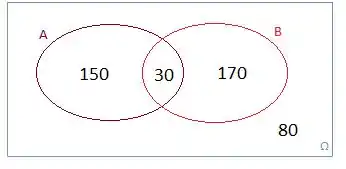
Já que 80 pessoas não compraram nenhum dos dois produtos.
Passo 3
O número total de entrevistados é a soma de cada região:
Resposta
Exercício Resolvido #6
Prova FGV-SP
Em uma pesquisa de mercado foram entrevistadas várias pessoas acerca de suas preferências em relação a três produtos, A, B e C. Os resultados da pesquisa indicaram que:
- 210 pessoas compraram o produto A
- 210 pessoas compraram o produto B
- 250 pessoas compraram o produto C
- 20 pessoas compraram os três produtos
- 100 pessoas não compraram nenhum dos três produtos
- 60 pessoas compraram os produtos A e B
- 70 pessoas compram os produtos A e C
- 50 pessoas compraram o conjunto B e C
Quantas pessoas foram entrevistadas?
Passo 1
Vaamos lá! Esse é um problema clássico que envolve conjuntos e probabilidade. Temos três conjuntos, que possuem (ou não) interseção.
O primeiro passo é desenha-los e entender bem o que cada região significa
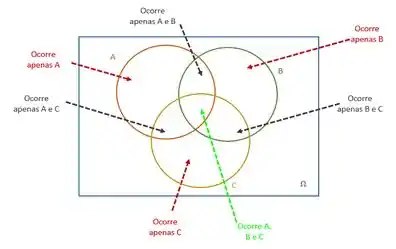
Passo 2
Agora que cada região está bem definida, vamos começar a completar o conjunto com os dados do enunciado. Existe uma ordem que é melhor para completar e torna todo o processo mais fácil.
1º Completar a região da interseção dos três conjuntos/eventos.
“20 pessoas compraram os três produtos”
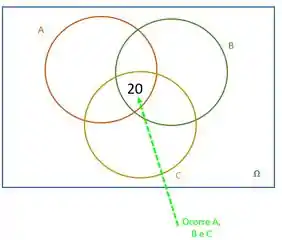
2º Completar as regiões das interseções duas a duas, tomando cuidado de não esquecer do valor já adicionado. Ou seja, pelo enunciado tempos:
60 pessoas compraram os produtos A e B Atenção! Está incluso nessas 60 pessoas as 20 pessoas que compraram A, B e C. Para saber quem comprou APENAS A e B devemos subtrair: 60-20 = 40 pessoas.
70 pessoas compram os produtos A e C Mesmo pensamento! Quem comprou APENAS A e C foram: 70-20 = 50 pessoas.
50 pessoas compraram o conjunto B e C Mesmo pensamento! Quem comprou APENAS B e C foram: 50-20 = 30 pessoas.
Então o diagrama vai ficar:
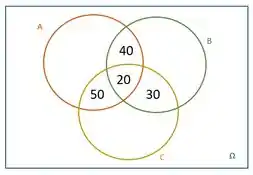
3º Completas as regiões que representam as pessoas que compraram apenas UM produto. Ou seja, compraram ou A ou B ou C.
A ideia é a mesma das regiões de interseção dois a dois. Devemos tomar cuidado pois o valor do enunciado não será o mesmo que escreveremos nessas regiões. Devemos subtrair dos valores já existentes ali.
Ficou confuso? Vamos pro diagrama!
“210 pessoas compraram o produto A”
“210 pessoas compraram o produto B”
“250 pessoas compraram o produto C”
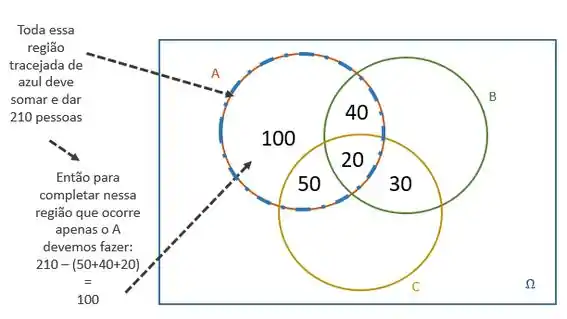
Seguindo o mesmo raciocínio para as outras regiões (B e C) teremos:
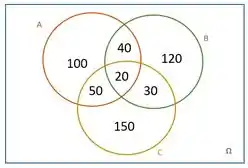
4º Completar com os elementos que não pertecem a nenhum desses conjuntos.
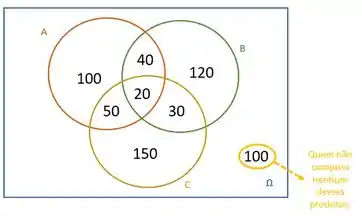
Passo 3
O número total de entrevistados é a soma de cada região:
Resposta
610 pessoas