Cálculo de Probabilidades - Introdução
Produzido por Jorge Alberto NascimentoTeoria
Introdução
Cara, sabe quando você está jogando algum jogo, e quer saber as chances de vencer? Ou então, quando lança um dado e quer saber a chance de sair o número 3?
É pra isso que a probabilidade serve! A probabilidade é uma forma de calcular as chances de algo que você quer que aconteça.
Como calcular?
Vamos falar de uma definição que é MEGA importante.
Do que eu estou falando? Tô falando daquele conceito clássico que você viu no ensino médio, onde seja um evento qualquer do espaço amostral . A probabilidade de ocorrer, denotada por , é dada por:

Resultados favoráveis são os que concordam com o evento, entende?
Tipo, no caso do evento , os resultados favoráveis seriam , que são os números pares do dado.
Exemplo: O estacionamento de um prédio possui vagas, para cada apartamento. Um morador novo chega ao prédio e sem saber quais vagas são suas resolve estacionar em qualquer uma. Qual a probabilidade de ele estacionar na vaga certa ?
Passo 1) Qual é o evento que queremos? .
Dados do problema:
(que são as vagas do cara)
(total de vagas)
Passo 2) Calculamos pela fórmula
Probabilidade de complementares
Lembra aquela história de eventos complementares? Por exemplo, um evento : sair números pares num dado é complementar ao evento : sair números ímpares num dado.
Uma coisa legal à respeito disso é que:
E isso fica claro olhando nosso diagrama aqui em baixo:
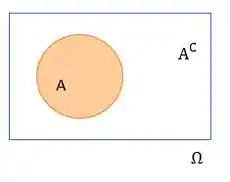
Temos que , já que é todo nosso espaço amostral! Então:
Pra NUNCA se esquecer
Cara, você nunca, NUNCA, NUUUUNCA pode se esquecer do seguinte:
Porque afinal de contas, a probabilidade de um evento acontecer tá sempre entre (nenhuma chance) e .
Pode parecer óbvio, mas muita gente erra e os professores adoram dar zero em quem escreve probabilidades maiores que ou probabilidades negativas, então toma cuidado em!
Outra parada muito importante, é a seguinte propriedade:
Isso aí ocorre justamente por aquela propriedade de conjuntos muito semelhante a isso que vimos anteriormente!
Dados e Tabelas
Cara, nesse tipo de questão iremos usar COM CERTEZA aquela fórmulinha lá:
Isso vai acontecer pois estamos trabalhando com dados e/ou tabelas, ou seja, tudo quantitativo. Iremos trabalhar com a quantidade de pessoas, de grupos que realizam certas atividades.
O importante aqui é ter calma na hora de analisar nosssa tabela ou dado. Primeiro procure o evento em questão e depois busque o espaço amostral. Geralmente o espaço amostral vai ser constituído de uma soma (do seu evento e do complementar dele).
Ex.:
Considere o lançamento de um dado e os seguintes eventos relacionados a esse experimento aleatório.
Determine agora:
e ;
Sabemos que:
Opa, e o ?
Bom, quando um dado pode cair com o número ?? Nunca né? Então esse conjunto que representa nosso evento será um vazio!
Logo:
E:
Note que estamos realizando uma análise QUANTITATIVA. Estamos olhando quantas vezes o evento A ocorre para enfim substituirmos na nossa expressão clássica!
Vamos praticar um pouco mais!
Probabilidade de complementares
Pra NUNCA se esquecer
Dados e Tabelas
Exercícios Resolvidos
Exercício Resolvido #1
Marcos Nascimento Magalhães e Antonio Carlos Pedroso de Lima, Noções de Probabilidade e Estatística, 6ª ed. São Paulo: Edusp, 2004, 56-29
Um candidato a motorista treina na auto-escola e acredita que passa no exame com probabilidade 0,7. Se não passar, fará mais treinamento, o que ele estima que lhe aumentará em 10% a probabilidade de passar, isto é, no segundo exame passará com 0,77 de probabilidade.
Supondo que ele continue acreditando nesse aumento de possibilidade, em que exame será aprovado com certeza?
Passo 1
Pra essa questão, nada melhor do que montar um diagrama. Olha só:

O enunciado diz que a cada vez que ele reprova, aumentam as chances dele passar em 10%.
Ou seja, na segunda tentativa ele terá uma probabilidade de passar de: 0,70.1,1=0,77
Na terceira: 0,77.1,1 = 0,847
Na quarta: 0,847.1,1=0,9317
Na quinta 0,9317.1,1=1,02487 ou seja, na quinta tentativa a chance dele passar ultrapassa 1, ou seja, ultrapassa 100%. Isso quer dizer que com certeza ele será aprovado.
Resposta
5ª tentativa.
Exercício Resolvido #2
Elaboração própria.
Retira-se uma carta de um baralho. Qual a probabilidade da carta retirada ser uma dama ou uma carta de copas?
Passo 1
Definir os eventos:
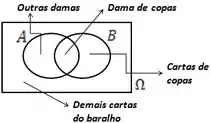
O que queremos?
Probabilidade de ser um ou outro.
Sabemos que:
Passo 2
Determinar e
Se você não se lembra bem, um baralho é composto por 52 cartas, divididas em 4 naipes (espadas, copas, paus e ouros). Cada um desses naipes possui 13 cartas, (às, 1, 2, 3..., 10, dama, valete e rei). Então temos 4 damas totais em um baralho, uma de cada naipe.
Como são 4 damas em 52 cartas,
Como cada naipe possui 13 cartas,
E:
Lembrando que a interseção é a dama de copas.
Passo 3
Substituir na fórmula inicial.
Resposta
Exercício Resolvido #3
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 115-15
Considere um urna contendo três bolas pretas e cinco bolas vermelhas. Retire duas bolas da urna, sem reposição.
a) Obtenha os resultados possíveis e as respectivas probabilidades.
b) Mesmo problema, para extrações com reposição.
Passo 1
a) Quero saber os meus resultados possíveis, ou seja, os eventos do meu espaço amostral. E além disso quero a probabilidade de cada um deles.
Vamos lá!
Na minha urna eu tenho 3 bolas pretas (PPP) e cinco bolas vermelhas (VVVVV). Então meus eventos possíveis serão:
{(PP); (PV); (VP), (VV)}
Agora vamos calcular as probabilidades:
Sabemos que , logo em um caso SEM reposição teremos:
Evento A (PP):
Evento B (PV):
Evento C (VP):
Evento D (VV):
Note que: no caso sem reposição a quantidade total de bolas varia e a quantidade de bolas de cada cor depende da cor que foi retirada anteriormente.
Passo 2
b) Em um caso COM reposição teríamos:
Evento A (PP):
Evento B (PV):
Evento C (VP):
Evento D (VV):
Note que neste caso a quantidade total de bolas não varia e a probabilidade da segunda independe da primeira retirada.
Resposta
a) Evento A :
Evento B:
Evento C:
Evento D:
b) Evento A:
Evento B:
Evento C:
Evento D:
Exercício Resolvido #4
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 124-41
Considere que a empresa M&B tenha 15.800 empregados, classificados de acordo com a tabela abaixo. Suponha que escolhamos dois empregados ao acaso, com reposição. Qual a probabilidade de que:

a) ambos sejam do sexo masculino;
b) o primeiro tenha menos de 25 anos, e o segundo seja do sexo masculino e tenha menos de 25 anos;
c) nenhum tenha menos de 25 anos.
Passo 1
a) Probabilidade de ambos empregados serem do sexo masculino
Sabemos que a probabilidade de um evento A é dada por:
Então teremos:
Evento W: Sortear dois funcionários homens
Passo 2
b) O primeiro tenha menos de 25 anos, e o segundo seja do sexo masculino e tenha menos de 25 anos;
Evento X: Sortear um funcionário que tenha menos de 25 anos
Evento Y: Sortear um funcionário homem que tenha menos de 25 anos
Assim, a probabilidade será:
Passo 3
c) nenhum tenha menos de 25 anos.
Agora vamos querer a probabilidade de sortear dois funcionários que tenha mais de 25 anos, ou seja, nenhum tenha menos de 25 anos.
Resposta
a)
b)
c)
Exercício Resolvido #5
UFRJ-PF-2015.1.-1
Em um bairro existem mil residências que podem ser atendidas por empresas de TV a cabo. A empresa tem assinantes, a empresa tem e a empresa tem assinantes, sendo que algumas residências em condomínios subscrevem aos serviços de mais de uma empresa. Assim, temos residências que são assinantes de e , de e , de e e que são assinantes das três empresas. Se uma residência desse bairro é sorteada ao acaso, qual é a probabilidade de:
- Ser assinante apenas da empresa ?
- Assinar pelo menos uma delas?
- Não ter TV a cabo?
Passo 1
Temos um total de residências que podem ser atendidas por três empresas de TV diferentes .
Vamos anotar os dados que o problema dá:
Esses são os totais de usuários de cada empresa... mas também temos usuários que usam serviços de mais de uma empresa. Esses valores nos dão:
Passo 2
Pra facilitar a gente a resolver todos os itens, vamos usar aquela ideia de conjuntos?
Vamos ter três conjuntos, um pra cada empresa, e já conhecemos todas as interseções.
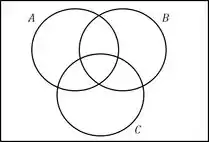
Para preencher começamos pela interseção entre as três empresas que vale e depois pelas interseções entre duas (descontando o ) e por fim pro valor total de assinantes de cada empresa (sem esquecer de descontar todas as interseções).
Por fim, ficamos com isso aqui:
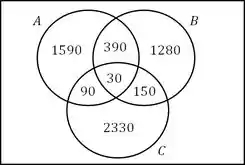
Passo 3
(a)
Olhando no nosso esquema de conjuntos, a gente vê que só residências são assinantes somente da empresa .
Então a probabilidade da escolhida ser assinante só de é:
Lembrando que é o total de residências.
Passo 4
(b)
Pra achar essa probabilidade, a gente precisa encontrar o número total de pessoas que assinam, certo? Afinal de contas, a probabilidade de pelo menos uma pessoa assinar é a probabilidade de ocorrerem assinaturas. Pra encontrar esse número, podemos somar todos os números que aparecem no nosso esquema de conjuntos ou utilizar a fórmula da união de conjuntos. Assim:
Mas veja, podemos obter essa resposta também usando:
E daí a probabilidade será:
Passo 5
(c)
Se o nosso esquema representa as residências que tem pelo menos uma TV à cabo, pra saber o total de residências sem nenhuma, é só fazer...
E daí a probabilidade vai ser:
Você poderia pensar também que:
E isso a gente tinha calculado antes:
Daí:
Resposta
Exercício Resolvido #6
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 125-49
Considere o quadrado com vértices (0,0), (1,0), (0,1) e (1,1). Suponha que a probabilidade de uma região A (evento) seja a área dessa região.
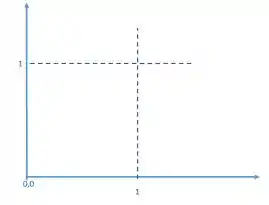
a) Represente graficamente o evento A = conjunto dos pontos cuja distância à origem seja menor ou igual a 1.
b) Calcule P(A)
c) Calcule a probabilidade do evento , onde b é um número tal que
d) Calcule , onde B foi definido em (c).
Passo 1
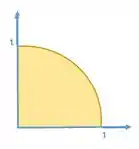
a)Represente graficamente o evento A = conjunto dos pontos cuja distância à origem seja menor ou igual a 1.
Pelo enunciado podemos notar que a região que delimita o evento A é uma curva, um segmento de circunferência, cujo evento A é toda área delimitada por essa curva.
Passo 2
b) Determine P(A)
Após entendermos quem é A, a probabilidade de A ocorrer será:
Onde utilizaremos a área como referência.
A área da região A é um quarto da área de uma circunferência de raio 1 e a área total é a área de um quadrado de lado 1.
Passo 3
c) Calcule a probabilidade do evento , onde b é um número tal que
Primeiramente vamos entender quem é esse evento B com uma figura:
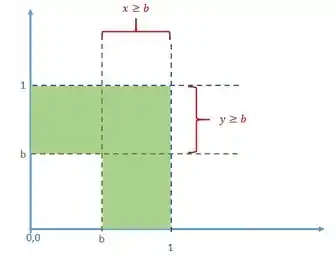
A área de vai ser essa área verde.
Repare que a área branca que restou embaixo à esquerda vale . Ou seja, como a área do quadrado vale , a área verde vale . Assim:
Passo 4
d) Calcule , onde B foi definido em (c).
Temos simplesmente
Que é justamente aquela área que calculamos antes, do quadrado branco que está embaixo à esquerda na figura.
Resposta
a)
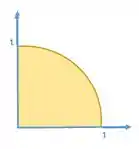
b)
c)
d)
Exercício Resolvido #7
UFRJ, ProbEst, P1/2013.1, 1
Para sagrar-se campeão de um torneio de tênis, um jogador precisa vencer quatro partidas sucessivas, todas elas eliminatórias. José é um dos participantes e suas probabilidades de vitória em cada partida (caso ele não tenha sido eliminado até então) foram estimadas em: 80% na 1ª partida, 70% na 2ª partida, 60% na 3ª partida (semifinal) e 50% na 4ª partida (final). Observe que estas probabilidades independem de quem seja o seu adversário em cada partida. Calcule as probabilidades de que José:
- Não consiga chegar até a final;
Passo 1
Fala Aíí!! Como no enunciado nos é dado a probabilidade de vitória em cada partida, iremos utilizar essas informações para resolver a questão, beleza?!
E como faremos isso?? Iremos calcular a probabilidade dele chegar na final e calcularemos o complementar disso. O complementar será a probabilidade dele não chegar na final. Show de bola?!

Primeiramente vamos montar o espaço amostral desse torneio de tênis.
Quais os resultados possíveis?
Então, o nosso espaço amostral é:
Passo 2
Agora vamos determinar a probabilidade de cada um desses resultados.
Se você reparar, no enunciado é dada a informação da probabilidade dele ganhar na primeira partida é de . Assim, a probabilidade dele perder de primeira é 1 menos a probabilidade dele ganhar a primeira partida, concorda? Portanto,
Belezinha?!
Seguindo o mesmo raciocínio, a probabilidade dele perder na segunda partida é igual a prob. de ele ganhar a primeira vezes a prob. dele perder a segunda:

Já ta dando pra pegar a ideia, né?! Vamos continuar com o mesmo racioncínio!!
A Probabilidade dele perder na terceira partida é a prob. de ele ganhar a primeira vezes a prob. de ganhar a segunda vezes a prob. de perder a terceira hahahahaha
Prob. de ele perder na quarta segue o mesmo raciocínio.
E a prob. de vencer o torneio é:
Assim já conseguimos calcular a probabilidade de cada um dos casos acontecerem.
Beleza?!
Passo 3
(a)
A questão nos pede para calcularmos a probabilidade dele não conseguir chegar a final.
Considerando:
A gente pode dizer que , concorda? São os dois casos que a pessoa pelo menos chega a final.
Então:
Passo 4
Mas o exercício pede a probabilidade do cara não chegar a final, ou seja:
Pelo que a gente sabe:
Logo, a probabilidade dele não conseguir chegar na final é 0,664 ou 66,4%.
Resposta
Exercício Resolvido #8
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006,110 -09
Problema 3: Três jogadores A, B e C disputam um torneio de tênis. Inicialmente, A joga com B e o vencedor joga com C, e assim por diante. O torneio termina quando um jogador ganha duas vezes em seguida ou quando são disputadas, ao todo, quatro partidas. Quais são os resultados possíveis do torneio ?
No espaço amostral do problema 3, atribua a cada ponto contendo K letras a probabilidade (assim, AA tem probabilidade ).
a) Mostre que a soma das probabilidades dos pontos do espaço amostral é 1.
b) Calcule a probabilidade de que A vença (um jogador vence quando ganha duas partidas seguidas). Em seguida calcule a probabilidade de que B vença.
c) Qual a probabilidade de que não haja decisão?
Passo 1
Vamos começar entendendo o problema 3.
Para terminar o torneio duas coisas podem acontecer:
- Vamos olhar para o caso e escrever os possíveis eventos do nosso espaço amostral:
(AA) o jogador A ganhou a primeira partida contra B e a segunda contra C.
(BB) Análogo ao caso AA. O jogador B ganhou a primeira partida contra A e a segunda contra C.
(ACC) O jogador A ganhou a primeira partida contra B, mas perdeu a segunda contra C. Já C, ganhou a segunda partida contra A e ganhou a terceira partida que foi contra B.
(BCC) Análogo ao caso ACC.
(ACBB) O jogador A ganhou a primeira partida contra B, mas perdeu a segunda contra C (que foi o vitorioso). Contudo, o C perdeu a terceira partida contra B, que foi o vitorioso. B por sua vez, que ganhou a terceira partida, disputa a quarta com A e ganha.
(BCAA) Análogo ao caso ACBB.
Passo 2
- Vamos olhar para o caso (ii) e escrever os possíveis eventos:
(ACBB) O jogador A ganhou a primeira partida contra B, mas perdeu a segunda contra C (que foi o vitorioso). Contudo, o C perdeu a terceira partida contra B, que foi o vitorioso. B por sua vez, que ganhou a terceira partida, disputa a quarta com A e ganha.
(BCAA) Análogo ao caso ACBB.
Esses dois eventos nós já vimos no caso 1, pois atendem aos dois eventos pensados, belezinha?!
Continuando...
(ACBA) O jogador A ganhou a primeira partida contra B, mas perdeu a segunda contra C (que foi o vitorioso). Contudo o C perdeu a terceira partida contra B, que foi o vitorioso. B por sua vez, que ganhou a terceira partida, disputa a quarta com A e perde.
(BCAB) O jogador B ganhou a primeira partida contra A, mas perdeu a segunda contra C (que foi o vitorioso). Contudo o C perdeu a terceira partida contra A, que foi o vitorioso. A por sua vez, que ganhou a terceira partida, disputa a quarta com B e perde.
Show de bola?!
Passo 3
Beleza! Agora que conhecemos os possíveis resultados, podemos calcular a probabilidade de cada um ocorrer seguindo a regra do enunciado: atribua a cada ponto contendo K letras a probabilidade (assim, AA tem probabilidade ).
Assim:
- K=2
- K=3
- K=4
P(AA)
P(BB)
P(ACC)
P(BCC)
P(ACBB)
P(BCAA)
P(ACBA)
P(BCAB)
Então a soma das probabilidades é:
Pronto, provamos o que foi pedido na letra (A)!
Passo 4
b)
Na letra (B) precisamos calcular a probabilidade de que A vença (um jogador vence quando ganha duas partidas seguidas). Em seguida, calcular a probabilidade de que B vença.
Se você reparar, a probabilidade de A vencer será:
Da mesma forma, a probabilidade de vencer será:
Show de bola?!
Passo 5
c)
Neste caso, queremos saber a probabilidade de termos quatro partidas sem nenhum vencedor. Isso acontecerá quando forem disputadas, ao todo, quatro partidas, porém não houve nenhum vencedor. Para isso vamos utilizar os dois possíveis cenários:
Resposta
a)
A soma das probabilidade dá
b)
c)
Exercício Resolvido #9
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 125-45
Um inspetor da seção de controle de qualidade de uma firma examina os artigos de um lote que tem peças de primeira qualidade e peças de segunda qualidade. Uma verificação dos primeiros artigos selecionados ao acaso do lote mostrou que todos eram de segunda qualidade . Qual a probabilidade de que entre os dois próximos artigos selecionados, ao acaso, dos restantes, pelo menos um seja de segunda qualidade?
Passo 1
Vamos lá!! Queremos saber qual a probabilidade de que entre os dois próximos artigos selecionados, dos restantes, pelo menos um seja de segunda qualidade.
Eeepa! Nós lemos um pelo menos? Siim!

Quando falamos “pelo menos” temos que nos lembrar da ideia que é: pensar no problema inverso. Ou seja, se ele quer que pelo menos um seja de segunda qualidade, o meu problema inverso será: Nenhum artigo de segunda qualidade!
E como vamos calcular essa probabilidade?
Passo 2
Vamos entender e escrever o que está acontecendo...
O enunciado diz que existem artigos de primeira e segunda qualidade, sendo:
Então, podemos concluir que o total de artigos é .
Em seguida, o enunciado fala que retiramos artigos, ou seja, agora nossa quantidade total de artigos é:
Além disso, ele diz que esse artigos retirados eram todos de segunda qualidade, o que nos mostra que ainda existem na amostra artigos de primeira qualidade, certo?

Bom, vamos colocar aqui as nossa quantidades atuais de cada coisa:
- Artigo de primeira qualidade:
- Artigo de segunda qualidade
Total de artigos:
Passo 3
Vamos chamar nossos eventos de evento A e B:
Para calcular a probabilidade de não sair nenhum de segunda qualidade é só forçar ambos serem de primeira qualidade, concorda?
Podemos fazer isso da seguinte forma:
Primeiro vamos forçar o evento :
Beleza?!
Passo 4
Da mesma forma, forçando ainda mais a barra para o evento também acontecer, teremos:
Show de bola?!
Passo 5
Assim, para a retirada dos dois teremos:
Passo 6
Agora vamos utilizar o complementar!! A resposta será então: