Teoria
Fala aí, seja bem vindo ao Responde Aí! Vamos aprender tudo sobre Quartil?!
O que são Quartis?
Os quartis são valores que dividem uma amostra de dados em quatro partes iguais. Assim:
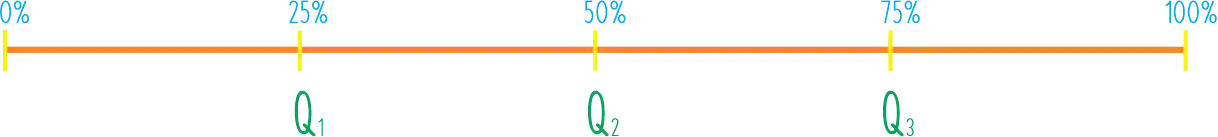
Na figura acima temos uma reta representando um conjunto de
- 1º quartil,
, é o valor da posição central entre o primeiro termo e a mediana. Ele serve para marcarmos que, até o seu valor, temos dos nossos dados;
- 2º quartil,
, é a a mediana;
- 3º quartil,
, é o meio do caminho entre a mediana e o último termo. Ele marca que, até o seu valor, temos dos nossos dados.
-Mas pra que servem os quartis?!
Imagina comigo a seguinte situação: Você está fazendo uma pesquisa e precisa dividir a população de forma que você consiga determinar a partir de qual valor (ou posição) temos a parte da população com maior renda. Como podemos descobrir isso?
Utilizaremos os famosos quartis! Com eles podemos rapidamente avaliar a dispersão e a tendência central de um conjunto de dados, que são etapas importantes na compreensão dos nossos dados.
📢 Clique para ver mais:
- 1º, 2º e 3º Quartil e Distância Interquartil: Exercícios Resolvidos;
- Medidas de Dispersão;
- Medidas de Centralidade.
Nesse vídeo abaixo a gente fala um pouco mais sobre os Quartis e como calcula-los com exemplos! Dá só uma conferida! 😉
Como calcular os Quartis?
Pra a gente aprender na prática como calcular os Quartis, vamos ver um exemplo!
Vamos supor que só tenham
Quais são os 1º, 2º e 3 quartis?
A primeira coisa que precisamos fazer é colocar os valores em ordem crescente:
Como Calcular o 1º Quartil
Com os valores organizados em ordem crescente, a gente calcula a mediana!
Para calcular a mediana é só a gente encontrar o valor do meio da lista:

Para encontrarmos o primeiro quartil, vemos qual é o valor entre o primeiro dado e a mediana
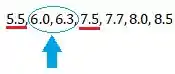
Não temos exatamente um carinha no meio, mas sim esses dois aí. Nesse caso, vamos tirar a média entre eles!
Como Calcular o 2º Quartil
O 2º quartil é a mediana, então já encontramos ele lá em cima!

Então temos:
Como Calcular o 3º Quartil
O terceiro quartil é o valor da posição central entre a mediana e o último termo. Até seu valor, temos 75% dos nossos dados.

Logo:
Fórmula geral para calcular Quartis
Os quartis são calculados quando temos uma sequencia de valores em ordem crescente.
O primeiro quartil é o valor que fica no meio do primeiro valor e da media. A posição do primeiro quartil pode ser calculada com a fórmula:
E a posição do terceiro quartil:
Distância Interquartil
Agora, digamos que você queira ver a quantidade de dispersão no meio, 50%, de um conjunto de dados. Para isso, utilizaremos a distância interquartil.
Em outras palavras, é a distância entre o primeiro quartil e o terceiro quartil:
No exemplo anterior, a gente poderia calcular a distância interquartil assim:
E é isso! Tranquilo, não é?! Agora vamos praticar com exercícios?!
Como calcular os Quartis?
Distância Interquartil
Exercícios Resolvidos
Exercício Resolvido #1
João Ismael D. Pinheiro, Probabilidade e Estatística: Quantificando a incerteza, Rio de Janeiro: Elsevier Editora Ltda, 2012, pp. 381-06.
A tabela de dados brutos a seguir reporta, o número de linhas telefônicas por 1000 habitantes em cada estado do Brasil, em 2001.
b) Determine os seus quartis
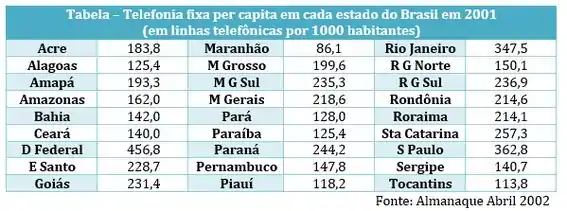
Passo 1
Bom, a primeira coisa que devemos fazer para determinar os quartis é colocar nossos dados em ordem crescente:
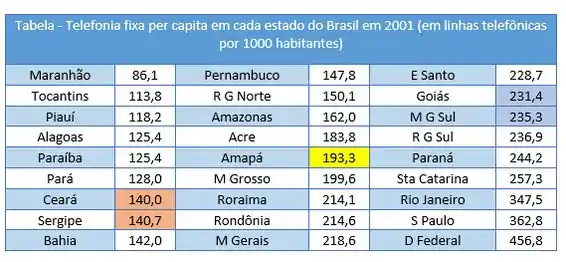
Passo 2
Temos que .
- Para encontrar Q1 faremos:
- Para encontrar Q3 faremos:
Isso quer dizer que Q1 vai estar entre a posição 7 e a posição 8, fazendo a interpolação:
Passo 3
Isso quer dizer que Q3 vai estar entre a posição 20 e a posição 21. Fazendo a interpolação:
Resposta
Exercício Resolvido #2
João Ismael D. Pinheiro, Probabilidade e Estatística: Quantificando a incerteza, Rio de Janeiro: Elsevier Editora Ltda, 2012, pp. 381-04.
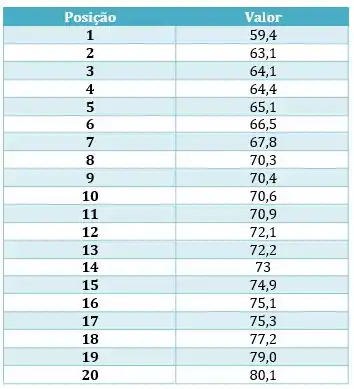
Um determinado fabricante produz implantes mamários utilizando gel de silicone. Os dados a seguir se referem a tensão de ruptura desses implantes e foram obtidos através de testes físicos realizados com uma amostra de tamanho n=20:
![]()
Com base nesses dados obtenha os quartis Q1,Q2 e Q3.
Foi apresentada a seguinte solução:

Posição (Q2)=
Posição (Q1) =
Posição (Q3) =
a) Algo está errado nessa solução. O que é?
b) Qual a solução correta?
Passo 1
a) E aí? Está errada a solução? Sim!
Está errada pois ele esqueceu de ordenar em ordem crescente! Esse é o primeiro passo, depois isso as coisas desandaram.
Passo 2
Vamos colocar na ordem crescente e calcular os quartis.
Passo 3
Agora vamos calcular os quartis.
- Q2
Sabemos que Q2 é a mediana, neste caso como temos um total par de números
Passo 4
- Q1
Temos um total de 20 posições, portanto
Faremos
Portanto o Q1 está entre a posição 5 e 6.
Fazendo a interpolação
Passo 5
- Q3
Para o cálculo de Q3 faremos primeiro
Isso quer dizer que Q3 está entre o 15 e o 16.
Fazendo a interpolação
Resposta
Exercício Resolvido #3
UFRJ, ProbEst, P2/2013.2, 1
Dado um conjunto de pares , variando de 1 até .
- Que relação existe entre as médias das variáveis e , onde é uma constante (isto é, )? E entre as variâncias de e ? E entre as distâncias interquartis (DIQ) de e ? Qual o coeficiente de correlação de e ?
- Responda as mesmas quatro perguntas do item (a) se , onde é uma constante positiva.
Passo 1
(a)
Bom, temos que , ou seja, estamos somando uma constante ao nosso valor de . Pensa comigo para medidas como média, quartis e tals, a relação entre e Y vai ser só somar a constante também, concorda? Se a média de X é um valor, a média de Y vai ser essa valor mais a constante.
Mas quando a gente for fazer o DIQ, a gente vai subtrair Q3 de Q1 e a constante vai sumir, então:
Já a variancia, assim como o coeficiente de correlação não são afetados pela soma de uma constante, confia em mim.
E:
Passo 2
(b)
Agora é outra história, estamos multiplicando por uma constante .
Medidas como média e quartis vão manter a mesma proporção, é só multiplicar por .
Com relação ao também manterá a mesma relação quando diminuir de .
Se você lembrar das propriedades da variância vai se ligar que:
Quando multiplicamos uma variável por uma constante, também não alteramos a correlação, que continuará sendo 1.
Resposta
Exercício Resolvido #4
Elaboração Própria
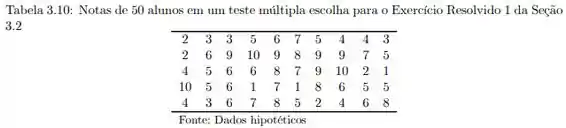
Considere novamente as notas dos 50 alunos, reproduzidas na Tabela 3.10. Calcule o intervalo interquartil das notas.
Passo 1
Primeiro temos que colocar esses dados em ordem, mas como tem muiiito dado pra gente reescrever, vamos usar aquele conceito de frequência para representá-los:
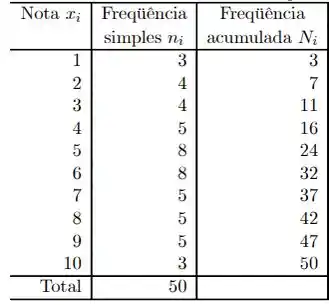
Nós escrevemos todos os valores de notas que aparecem nos dados e ao lado representamos a frequência simples de cada um, ou seja, quantas vezes cada um aparece. A última coluna, de frequência é simplesmente a frequência simples do analisado somada a todas as frequências simples anteriores.
Ok, voltando a questão, para calcular a distância interquartil temos que lembrar que:
Vamos começar calculando , nosso terceiro quartil. Ele deve estar na posição:
Onde é o número total de dados. No nosso caso :
Temos que fazer uma média ponderada entre o e o dado da tabela.
Olhando nossa tabela de freqüências, temos que procurar onde está o os dados e nas freqüências acumuladas.
Podemos observar que a frequência acumulada se torna para , então quanto terminamos de contar todas as notas até o temos dados. Então o dado vai ser e é o dado que temos imediatamente após o , já que é o último , ou seja, o dado é o .
Fazendo a média interpolada para , estamos mais perto do º (que vale )e mais perto do (que vale ), então:
Mas repara comigo, nessa tabela a gente só tem números inteiros, o valor nem existe nela. Então para tudo fazer mais sentido, vamos considerar que o terceiro quartil é isso aí arredondado mesmo:
Passo 2
Agora o primeiro quartil, a posição dele é dada por:
Mas olhando na tabela vemos que tanto o como o dado valem . Então de cara podemos afirmar que:
Portanto nossa é: