Estimadores
Teoria
Introdução
Cara, lá na parte de estatística da matéria, nós vimos que muitas vezes estaremos trabalhando com amostras, porque é muito difícil coletar informações da população, certo?
Só que, ao trabalhar com as amostras, nós só temos os parâmetros de média, variância, desvio-padrão amostrais, e não os parâmetros da população.
O que a gente vai fazer agora é estimar parâmetros da população, a partir dos dados das amostras! Como assim?! Vamos ver um exemplo!!!
Exemplo
Digamos que um engenheiro metalúrgico está interessado em analisar a porcentagem de carbono em uma liga de ferro produzida por sua empresa. Dez unidades amostrais de ferro apresentam as seguintes quantidades de carbono (em gramas) para cada cem gramas da liga:
Nesse caso, seria uma variável aleatória que indica a porcentagem de carbono nas ligas de ferro produzidas pela empresa (que é nossa população)...
Poderíamos representar nossa amostra aleatória por , já que são 10 observações. Logo nosso número de amostra n é 10.
Beleza até aqui?
Vamos agora ao problema: o engenheiro quer saber a quantidade média de carbono na liga de ferro que a empresa produz, ou seja, ele quer saber a média da população (), mas para descobrir isso precisaríamos descobrir os dados de toda a população!
Nós não sabemos o valor de , certo? Mas, calma! Podemos estimá-lo a partir da amostra...
Adivinha como?
O valor da média amostral, , é uma estimativa do parâmetro .
Quando maior o nosso número de amostra melhor será a nossa estimativa!
Voltando ao nosso exemplo, vamos calcular a média amostral:
E como foi dito, podemos usar essa estimativa para representar o valor da média populacional , então:
OBS: Uma confusão não tão difícil de acontecer é confundir o conceito de estimador com o conceito de estimativa. Pensa assim: estimador é o parâmetro amostral, e o valor desse parâmetro é a estimativa. Então no exemplo que vimos:
Beleza?!
Estimadores Naturais
Isso aí que escrevemos ai em cima é verdade porque a média amostral é um estimador natural de que é a média populacional. Show de bola?!
Dá mesma forma, vamos ter outros parâmetros amostrais que serão estimadores naturais dos seus respectivos parâmetros populacionais, vamos conhecê-los:
Variância Amostral/Variância Populacional
A variância amostral é um estimador natural para a variância populacional :
Desvio Padrão Amostral/Desvio Padrão Populacional
O desvio padrão amostral é um estimador natural para o desvio padrão populacional
Proporção Amostral/Proporção Populacional
Vamos ver (ou relembrar) o que são esses caras agora rapidinho?!
Supondo uma população de pessoas onde 5 delas são ruivas. Nossa proporção populacional de pessoas ruivas seria então:
E se dessa população fosse retirada uma amostra de 100 pessoas, e 3 delas fossem ruivas, nossa proporção amostral de pessoas ruivas seria:
A proporção amostral é um estimador natural para a proporção populacional
Amostra Obtida de uma População Normal
Beleza, vimos como estimar valores de parâmetros populacionais usando a amostra. E se eu quisesse o contrário? Se eu conhecesse minha população, mas não tenho os dados amostrais e quero estimá-los? Vamos ver isso agora!
Digamos por exemplo que eu conheço a média populacional e quero encontrar a média amostral , como no exemplo:
Uma população de abóboras tem peso médio igual a e desvio padrão de . É retirada uma amostra de 30 abóboras desta população. Estime a distribuição da média amostral, assim como sua esperança, variância e desvio padrão.
Foi dito que:
Vamos supor uma amostra aleatória de elementos, ou seja, é uma amostra aleatória obtida de uma população Normal. Quando temos esse tipo de situação sabemos que é uma v.a. .
Com isso, todas as ’s tem a mesma distribuição .
Se quiséssemos calcular a média amostral dessa amostra teríamos que:
Tá mas o que vamos fazer com isso?
Repara que aqui estamos trabalhando com a média amostral, e pelo teorema central do limite, se o número de amostras for pelo menos , podemos dizer que a média amostral segue uma distribuição normal onde:
Ou seja, pelo próprio TCL, podemos indicar que a média amostral segue uma normal.
E também podemos encontrar sua esperança e desvio padrão.
E podemos encontrar também sua variância, dividindo o desvio padrão, pela raiz de :
Recapitulando:
Usando propriedades de esperança e variância:
Olhando para o exemplo anterior temos que nossa média amostral vai seguir a distribuição...
Com essas informações, podemos estimar o valor do estimador por meio dessa distribuição de probabilidade:
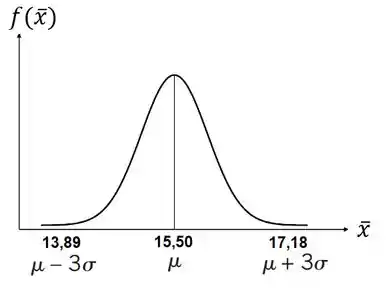
Não precisa encrencar com esse não. Isso aí é só pra ilustrar melhor todo o intervalo de valores que nosso estimador pode ter.
Como numa distribuição Normal aproximadamente dos valores estão no intervalo ; , estamos garantindo que nossa média amostral tem de chances de estar entre e .
Estimação da Proporção Amostral
E se a gente quisesse fazer a mesma coisa para o estimador ? Vamos tentar outro exemplo:
“Numa população de crianças, quer ser bombeiro(a) ou astronauta quando crescer. Retira-se uma amostra de 200 crianças dessa população. Qual a probabilidade da proporção amostral de crianças que quer ser bombeiro(a) ou astronauta ser maior que ?”
A gente pode definir também a esperança e a variância da proporção amostral:
Ou seja:
Isso acontece por causa do Teorema Central do Limite, mas não se preocupa muito com isso: foca nas contas!
Como vimos, vai seguir uma distribuição Normal. Os parâmetros serão:
Ou seja:
Queremos saber a probabilidade de ser maior que :
Como segue uma Normal, padronizamos isso daí:
Procurando essa probabilidade na tabela da Normal, temos que:
Vamos treinar isso tudo nos exercícios agora!
Estimadores Naturais
Amostra Obtida de uma População Normal
Estimação da Proporção Amostral
Exercícios Resolvidos
Exercício Resolvido #1
João Ismael D. Pinheiro, Probabilidade e Estatística: Quantificando a incerteza, Rio de Janeiro: Elsevier Editora Ltda, 2012, pp. 362.
Um pesquisador está estudando a resistência de um certo material sob determinadas condições. Ele sabe que essa variável é Normalmente distribuída com variância igual a 4 unidades². Foi extraída uma amostra aleatória de tamanho 10 obtendo-se os seguintes valores:
- Calcule a estimativa pontual da media populacional, com base nessa amostra.
Passo 1
(a)
A estimativa pontual para a média populacional é qual? A média amostral, concorda?
Então, nossa estimativa pontual será:
Resposta
Exercício Resolvido #2
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006,296-3
Suponha um experimento consistindo de provas de Bernoulli, com propriedades de sucesso . Seja X o número de sucessos, e considere os estimadores
a)
b)
Determine a esperança e variância de cada estimador. Por que não é um “bom” estimador?
Passo 1
Vamos olhar para cada um separadamente para poder comparar os mesmos ok?
-
Como não possui restrição nenhuma, ou seja, estamos olhando para todas as tentativas, podemos perceber que temos uma Distribuição Binomial.
E sabemos que em uma binomial,
Passo 2
Portanto
Como
E
Passo 3
Olhando para ... Vamos identifica-lo?
Note que pela restrição de somente o primeiro resultado importa. Se ele for sucesso dizemos que e caso seja fracasso . Por essa restrição notamos que temos um experimento de Bernoulli para , que é o resultado da primeira prova.
Sabemos que em Bernoulli
Passo 4
Vamos calcular para avaliar melhor .
Passo 5
Comparando e notamos que só assume valores 0 ou 1, pois só observa o primeiro resultado, o que mostra que ele é um pior estimador. Além disso pelas nossar contas vimos que , ou seja, sua variância será sempre maior que do estimador (para todo n maior que 1 né!).
Resposta
é o pior estimador.
Exercício Resolvido #3
Elaboração Própria
Suponha que segue uma distribuição Normal de média e desvio padrão .
Temos uma amostra de unidades de , e os valores de são independentes.
Determine a distribuição da média amostral e seus parâmetros, sua esperança e sua variância.
Passo 1
Sabemos que:
Aqui temos que lembrar de como lidamos com uma amostra a partir de uma população normal. Se criarmos uma v.a. que represente a soma de todos os da nossa amostra:
Pelo Teorema Central do Limite, sabemos que a distribuição de também é uma Normal, onde os parâmetros vão ser:
A média amostral é a soma das v.a.s divida pelo tamanho da amostral, certo? Mas já é a soma das v.a.s, então:
Ué, se é uma distribuição Normal dividida por um número , também vai seguir uma distribuição Normal!
Passo 2
Para descobrir a esperança e a variância de vamos “aplicar” esperança dos dois lados da equação:
Usando as propriedades:
Vimos lá em cima que , então:
Para a variância, vamos fazer a mesma coisa:
Usando as propriedades, o sai ao quadrado:
Como vimos, , então:
Resposta
Exercício Resolvido #4
Elaboração Própria
Suponha uma população de estudantes. Queremos saber qual a média populacional da idade desses estudantes. Tomamos uma amostra de 10 estudantes e observamos as seguintes idades:
Não temos informações sobre a população, só sobre a amostra. É possível estimar o valor da média populacional mesmo assim? Como se chama esse estimador e de qual tipo ele é?
Passo 1
Podemos, certo? A média amostral é um estimador natural da média populacional. Então:
Então é a estimativa que temos para o valor da média populacional das idades!
Resposta
Média amostral
Estimador natural
Exercício Resolvido #5
Elaboração Própria
Qual a diferença entre parâmetro, estimador e estimativa? Dê exemplos.
Passo 1
Parâmetros são dados sobre a nossa população ou amostra, portanto podem ser populacionais ou amostrais. Como exemplo temos as médias e .
Estimador é um parâmetro amostral que é usado como aproximação para o valor de um parâmetro populacional. Por exemplo, o desvio padrão amostral é uma estimador para o desvio padrão populacional .
Estimativa é o valor do nosso estimador, é o número propriamente dito. Por exemplo, calculamos que a variância amostral da nossa amostra vale , isso quer dizer que é a estimativa para o valor da variância populacional .
Resposta
Ei, a resposta está no passo a passo :)