Intervalo de Confiança para Média com σ Desconhecido
Teoria
Fala Aíí!!! Digamos que você tem uma empresa e tenha medido o tempo médio que 26 funcionários necessitavam para realizar um tarefa. Dessa amostra foram obtidos os seguintes resultados:
Onde é a média amostral e o o desvio padrão amostral. Aí digamos que o seu sócio queira que você construa um intervalo de confiança de 95% para o tempo médio de realização da tarefa. Como você faria isso?
Se você reparar, nós não temos a informação do desvio padrão populacional nesse caso. Quem poderá nos defender agora?
O Intervalo de Confiança
Bom, para o intervalo de confiança vamos encontrar da mesma forma que fizemos quando conheciamos o desvio padrão populacional :
Onde é margem de erro.
Beleza... mas o valor de pra quando a gente conhece o desvio padrão , é:
Mas agora como não temos o valor do desvio padrão, iremos substituir pelo desvio padrão amostral , nossa fórmula pra ficará:
Além disso, você deve estar se perguntando o porquê de no lugar do “z” ter um “t”... Calma! Não foi erro de ortografia! É que agora vamos substituir também a distribuição Normal pelo .
Opa, mas como funciona essa distribuição ? Já já veremos, my friend!! Por enquanto vamos fazer limonada com os limões que temos: vamos substituir na fórmula da margem de erro todos os valores que conhecemos:
Sabemos o valor de e . Se você reparar, se tivermos o valor do nível de significância , teremos o índice do para utilizar . Dessa forma, conseguimos encontrar o valor de Siiim!! Isso vai ser igual ao que vimos no IC com desvio padrão conhecido!
Temos que
No nosso probleminha
Dessa forma, nossa margem de erro ficará:
Agora sim vamos precisar encontrar o ... E como faremos isso?
Vamos entender um pouco melhor sobre essa tal de ?!
t de Student
A distribuição t de Student terá a seguinte cara:
É muito parecida com a distribuição normal, concorda?
Essa distribuição é derivada da distribuição Normal, então algumas características são mantidas.
- O gráfico continua sendo simétrico e centrado no zero, ele só é um pouco mais aberto talvez.
- Podemos calcular a probabilidade vinculada a essa distribuição usando uma tabela também, que vai ser essa aqui debaixo:
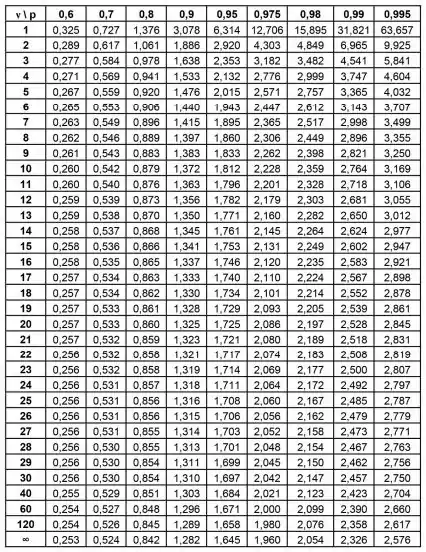
Pra gente conseguir encontrar o vamos precisar utilizar uma parada que é a ideia de números de graus de liberdade, representado pelo símbolo . A depende desse parâmetro .
Se o exercício não der o número de graus de liberdade, usamos como valor . No nosso exemplo, .
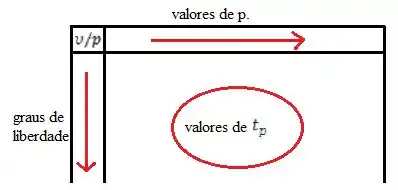
Vamos ver na prática como vamos utilizar então a tabela? Nós vamos seguir o fluxo desse desenho abaixo, mas quem vai ser e será o grau de liberade que falei anteriormente e é o índice do . No nosso problema
Assim, se buscando na tabela e , temos:
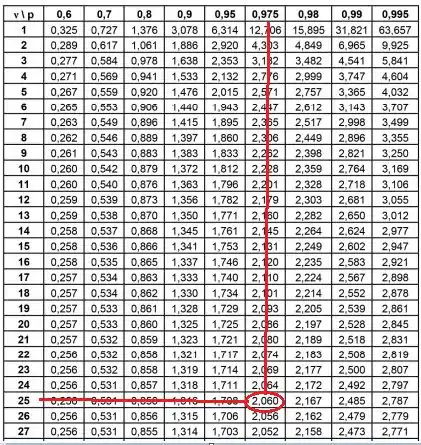
Ou seja, o nosso . Beleza?!
Agora vamos voltar pra nossa fórmula da margem de erro
Portanto, nosso IC:
Ou seja, nessa empresa, o tempo médio para realização dessa tarefa, em um intervalo de confiança de 95% está entre 19,22 e 23,56 minutos.
Beleza?!
Então o esquema é:
Conheço uso tabela da Normal
Não conheço uso a tabela do
Nos vemos nos exercícios!!!
t de Student
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Utilizando uma amostra aleatória com , foram obtidos os seguintes valores para a média e variância amostrais:
Para esse caso, construa um intervalo de confiança de nível de confiança 90% para a média populacional, .
Passo 1
O nível de confiança é de 90%...
Vamos procurar na tabela pelo valor de..
Passo 2
Pra montar o intervalo a gente tem que calcular o .
Passo 3
Pra finalizar, nosso intervalo será:
Resposta
Exercício Resolvido #2
Lista Regina – CEFET Intervalo de Confiança – T de Student
Um revista publicou um artigo que descreve várias caracterésticas de bastões combustíveis usados em um reator pertencente a uma usina nuclear. Medidas da porcentagem de enriquecimento de 12 bastões foram reportados como segue:
Encontre um intervalo de confiança de 99% para o percentual médio de enriquecimento. Você concorda com a afirmação de que o percentual médio de enriquecimento é de 2,95%? Por quê?
Passo 1
Dados que a gente tem no problema:
Aí a gente tem as medidas de enriquecimento desses 12 bastões.
E queremos um intervalo de confiança para o percentual médio de enriquecimento, com confiança de 99%.
Tá, primeira coisa que a gente tem que observar é que a gente não conhece o valor de , concorda? Isso é muito importante pra calcularmos o .
Já que a gente não conhece , a gente sabe que nosso terá a seguinte cara:
Vamos ter que calcular cada um desses valores.
Passo 2
Como a gente tem as medidas dos 12 bastões da amostra, podemos calcular algumas coisas da amostra:
Passo 3
Como a confiança é de 99%:
e...
Pra completar falta saber o número de graus de liberdade que será:
Agora olhando na tabela, cruzando a linha 11 com a coluna 0,995:
Passo 4
Podemos montar nosso intervalo agora:
Passo 5
O exercício pergunta se a gente concorda que a média seria 2,95%!
Bom, se você observar nosso intervalo de confiança, percebe que o 2,95 está dentro dele.
Então, concordamos que 2,95% possa ser o percentual médio de enriquecimento dos bastões, já que esse valor está dentro do intervalo de confiança de 99%.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
P2- 2013.2 – UFRJ - Intervalo de Confiança – T de Student
Sabe-se que a altura dos indivíduos de uma certa população é Normalmente distribuída. Em uma amostra aleatória de tamanho 16, obteve-se o seguinte intervalo de 95% de confiança para a altura média populacional (em ).
- Forneça estimativas pontuais para a altura média e para o desvio padrão da altura.
- Qual seria o novo intervalo se a confiança exigida fosse 99%?
- Qual deveria ser o tamanho de uma nova amostra para que o novo intervalo tivesse a mesma amplitude do intervalo anterior, porém agora com 99% de confiança, supondo que o desvio padrão populacional seja igual a ?
Passo 1
(a)
A gente tem o intervalo de confiança dado já para a média populacional.
A gente sabe que o intervalo é assim:
Então:
Somando as duas equações:
Passo 2
Substituindo a gente encontra .
Sabendo que a gente não conhece , a gente saca que esse intervalo é com desconhecido, e que com isso, a fórmula de é:
Como .
Usando a tabela de com 15 graus de liberdade , encontramos que:
Substituindo os valores podemos encontrar a estimativa que a gente quer pro desvio padrão, que é o .
Passo 3
(b)
A gente sabe que o intervalo é:
E que:
Sabemos também que:
A única diferença é que agora:
que eu fiz usando a tabela .
Passo 4
Agora é só jogar na fórmula:
Nosso intervalo então será:
Passo 5
(c)
Agora temos que . Conhecendo podemos usar a Normal.
Temos também que:
Passo 6
A amplitude inicial que temos é e queremos mantê-la neste caso. Concorda comigo que a amplitude é igual a duas vezes o valor de ? Beleza, então:
Continua valendo que
Lembrando que agora podemos usar a Normal, já que conhecemos .
Substituindo os valores descobrimos o .
Resposta
Exercício Resolvido #4
P2- 2014.2 – UFRJ Intervalo de Confiança – T de Student
Um procedimento químico utilizado por uma indústria gera em média de cloreto de sódio como produto final de uma reação. A quantidade de cloreto obtida a cada vez apresenta um comportamento aleatório , onde A partir de repetições do mesmo procedimento, obteve-se em média de cloreto.
- Calcule o intervalo de confiança de para . Interprete o resultado.
- Considere que a indústria modificou o procedimento anterior e agora a variância da quantidade de cloreto produzida não é mais conhecida. Com uma amostra de repetições desse novo procedimento, obteve-se média e desvio padrão amostrais respectivamente iguais a e . Obtenha o intervalo de confiança de para o que o novo procedimento é capaz de produzir.
- Com base nos itens anteriores, você acredita que o novo procedimento seja capaz de produzir, em média, uma quantidade de cloreto de sódio diferente da que era obtida anteriormente? Qual é o nível de confiança associado à sua conclusão? (Suponha que as seleções de amostra relativas aos dois procedimentos químicos tenham sido realizadas independentemente uma da outra).
Passo 1
(a)
Vamos montar um intervalo de confiança para a média de cloreto produzido.
Quais os dados que a gente tem?
A gente sabe que a quantidade de cloreto produzida segue uma distribuição Normal e conhecemos a sua variância e desvio padrão
Pra montar o nosso intervalo a gente tem também os dados de uma amostra de repetições do experimento, que tiveram uma média de de cloreto produzido.
Então:
Passo 2
Temos dois tipos de intervalo de confiança pra média:
- Quando a gente conhece o desvio padrão ;
- E quando a gente não conhece .
Nesse caso a gente conhece ... então nosso intervalo vai ter o seguinte formato:
Com:
Passo 3
Falta calcular .
O intervalo é de de confiança...
Aí você tem que procurar no interior da tabela da Normal pelo e achar qual que dá ele (ou o mais próximo dele), cruzando as linhas e colunas. Vou usar...
Passo 4
Agora a gente calcular o ...
E o intervalo:
Seu resultado pode variar dependendo de como você arredondar... mas acho que como a gente tá falando de (que já é algo pequeno), parar na primeira casa tá bom.
A interpretação que a gente pode dar é que a média de de cloreto produzido em todos os procedimentos estará dentro desses limites do intervalo, com nível de confiança de .
Passo 5
(b)
O exercício diz que agora o procedimento mudou e o dado no enunciado não é mais válido.
Já tá ligado o que que muda agora? A gente vai continuar tendo que fazer um intervalo de confiança pra média de cloreto produzido, só que agora a gente tá naquele segundo caso ali óh... quando a gente não conhece o .
O exercício dá pra gente alguns dados de uma amostra desse novo procedimento...
E vamos fazer nosso intervalo de confiança pra média com .
Passo 6
Nosso intervalo continua tendo o mesmo formato:
Só que agora o muda:
Ao invés da gente usar a Normal, vamos usar ... justamente porque a gente não conhece o .
Passo 7
Vamos calcular .
Falta mais uma coisa pra .... o grau de liberdade!
Aí você cruza a linha do com a coluna na tabela e acha o valor que a gente quer.... MAS OPA! Não tem linha do ..
Iéh, mas lembra? Quando é muito grande, tipo , podemos aproximar pela Normal.
E esse valor a gente já usou na letra (a).
Passo 8
Temos tudo, só correr pro abraço!
E aí:
Passo 9
(c)
Primeiro vamos relembrar qual o intervalo que a gente tem pras médias de cloreto produzido nos dois experimentos.
Pro velho experimento:
Pro novo experimento:
O exercício pergunta se a gente acredita que o novo procedimento vai produzir cloreto com uma média diferente da do velho experimento? Sim, né?
Se você reparar não existe interseção entre os dois intervalos, são totalmente diferentes. Então teoricamente os valores que as duas médias podem ter são totalmente diferentes, não tem como as duas médias serem iguais.
Concorda?
A pergunta que não quer calar é: qual o nível de confiança disso que eu estou falando? Com que certeza eu posso afirmar que as médias vão ser diferentes?
Vem comigo!
Passo 10
Os intervalos de confiança estão relacionados a um nível de confiança, certo? No nosso caso os dois são de de confiança.
Esse valor representa a probabilidade da média realmente ficar dentro do intervalo que a gente calculou.
E pra gente garantir que as médias dos procedimentos vão ser diferentes, a gente tem que garantir que as médias realmente vão ficar dentro dos intervalos que a gente calculou, já que esses intervalos não tem interseção, certo? Aceitou isso?
Vou chamar de:
Preciso garantir que os dois eventos, e , aconteçam.
Passo 11
Aí vem o último passo, o exercício diz que os procedimentos são independentes.
Daí:
E a gente viu que:
Então a certeza com que a gente pode afirmar que as médias serão diferentes é:
Resposta
Exercício Resolvido #5
Lista de Exercício de Intervalo de Confiança e Teste de Hipóteses, Monitora Juliana, UFPR
Dez mensurações são feitas para a resistência de um certo tipo de fio, fornecendo os valores . Suponha-se que ohms e ohms. Vamos supor que tenha distribuição e que desejemos obter um intervalo de confiança para , com coeficiente de confiança .
Passo 1
Se nosso nível de confiança é , nosso nível de significância vai ser:
Como não conhecemos o desvio padrão populacional, esse vai ser um IC dado por:
Sabemos que:
Passo 2
Então só falta o termo para completarmos a fórmula. Como :
é então o que temos que procurar na tabela T de Student. O grau de liberdade que queremos é:
Cruzando na primeira linha com na primeira coluna da tabela temos que...
Passo 3
Agora substituímos tudo na fórmula: