Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 10.Exercícios - Ex. 26
10-26.Um artigo na revista Technometrics(1999.Vol.41.pp.202-211)
esnudou a capacidade de um medidor em medir os pesos de duas folhas
de papel. Os dados sǎo mostrados a seguir.
a) Verifique a suposicao de que os dados de cada folha säo provenien-
tes de distribuicoes normais.
b) Teste a hipótese de que os pesos medios das duas folhas cio iguais
contra a altemativa de que saodiferentes(e suponha vanáncias iguais).
Use a =0,05 e considere vanáncias iguais. Encontre o valor P.
c) Repita o teste prévio com a-0.10.
d)Compare suas respostas para os itens (b) c (c) c expliquc por quc
eles são iguais ou diferentes.
e) Explique como as questoes dos itens (b)e (c) poderiam ser respon-
didas com intervalos de confianca.
Passo 1
Oi oi gente,
Vamos lá fazer mais uma questão passo a passo?
Vem comigo!
Dados:
A média é a soma de todos os valores dividida pelo número de valores:
A variância é a soma dos desvios quadrados da média dividida por . O desvio padrão é a raiz quadrada da variância:
Passo 2
Letra a:
Gráfico da probabilidade normal:
Os valores dos dados estão no eixo horizontal e as pontuações normais padronizadas estão no eixo vertical.
Se os dados contiverem n valores de dados, então as pontuações normais padronizadas são os valores z na tabela III correspondendo a uma área de (ou a área mais próxima) com .
A menor pontuação padronizada corresponde à menor quantidade de dados, a segunda menor pontuação padronizada corresponde ao segundo menor valor de dados e assim por diante.
Papel 1:
Papel 2:
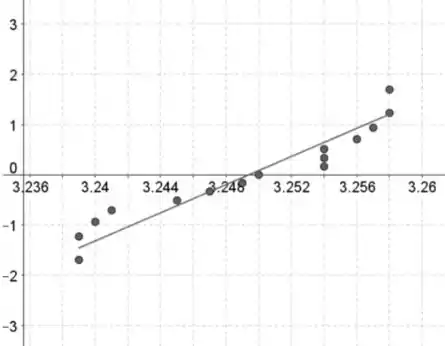
A suposição de normalidade parece válida porque os padrões nos gráficos de probabilidade normal são aproximadamente lineares e não continham nenhuma curvatura forte.
Passo 3
Letra b:
Determine as hipóteses:
Determine o desvio padrão agrupado:
Determine a estatística de teste:
Determine os graus de liberdade (arredondados para o número inteiro mais próximo):
Determine o valor P correspondente da tabela V :
Se o valor P for menor ou igual ao nível de significância, então a hipótese nula é rejeitada:
Existem evidências suficientes para apoiar a afirmação de que as médias da população são diferentes.
Passo 4
Letra c:
Se o Valor P for menor ou igual ao nível de significância, então a hipótese nula é rejeitada:
Existem evidências suficientes para apoiar a afirmação de que as médias da população são diferentes.
Passo 5
Letra d:
A conclusão na parte (b) e na parte (c) é a mesma, porque o valor P é extremamente pequeno e, portanto, menor do que ambos os níveis significativos.
Passo 6
Letra e:
Determine com usando a tabela IV:
Os pontos finais do intervalo de confiança para são:
Resposta
- Suposição satisfeita
- . Existem evidências suficientes para apoiar a afirmação de que as médias da população são diferentes.
- Existem evidências suficientes para apoiar a afirmação de que as médias da população são diferentes.
- A conclusão na parte (b) e na parte (c) é a mesma, porque o valor P é extremamente pequeno e, portanto, menor do que ambos os níveis significativos.