Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 10.Exercícios - Ex. 28

10-28. O "efeito mola" em um taco de golfe poderia ser detenninado

medindo o cocficiente de restituicão ta razão entre a velocidade de sa-

ída da bola e a velocidade de chegada de uma bola de golfe atirada na

cabeça do tacol. Doze tacos direcionadores, selecionados aleatoria

mente e produzidos por dois fabricantes de taco. são testados, sendo o

coeticiente de restituicāo medido. Os dados são:

a) Há evidência de que o cocficiente de restituição seja distribuído

aproximadamente de forma normal? Uma suposiçao de variâncias

iguais é justificada?

b) Teste a hipótese de que ambas as marcas de tacotém iguais coeficien-

les médios de restituição. Use a = 0.05. Qual é o valor P do teste?

c) Construa um intervalo de confianca de 95 para a diferenca média

entre as duas mareas de tacos de golfe.

d) Qual é a poténcia do tesle estatístico do item (b) para detectar uma

diferença verdadeira no coeficiente de restituicão de 0.2?

e)Que tamanho de amostra seria requeride para detectar uma diferen-

ça verdadeira nococficiente medio de restituição de O,1 com poten-

cia de aproximadamente 0.8?

Passo 1

Oi oi gente,

Vamos lá fazer mais uma questão passo a passo?

Vem comigo!

Sabemos que o tamanho da amostra é

n = n 1 = n 2 = 12

Médias da amostra:

x - 1 = 0.8406 + ⋯ + 0.7871 12 = 0.8161 x - 2 = 0.8305 + ⋯ + 0.8476 12 = 0.8271

e os desvios padrão

s 1 = 0.0217 s 2 = 0.0175

Passo 2

Letra a:

A suposição de normalidade parece razoável para ambas as amostras que verificaremos com base no gráfico de probabilidade normal.

Um gráfico de probabilidade normal é um método gráfico para determinar se os dados da amostra estão em conformidade com uma distribuição normal hipotética com base em um exame visual subjetivo dos dados.

Para construir um gráfico de probabilidade, as observações na amostra são primeiro classificadas do menor ao maior. Ou seja, a amostra x 1 , x 2 , . . . , x n é organizado como x ( 1 ) , x ( 2 ) , . . . x ( n ) onde x ( 1 ) é a menor observação, x ( 2 ) é a segunda menor observação, e assim por diante com x ( n ) o maior. A frequência cumulativa para observação x ( i ) é

i - 0.5 n

Uma probabilidade normal é construída em eixos ordinários traçando as pontuações normais padronizadas z i contra x ( i ) onde as pontuações normais padronizadas satisfazem

i - 0.5 n = P Z < z i = Φ z i

Nos eixos horizontais estão os valores x 1 , x 2 , . . . , x n . Se a distribuição hipotética descreve adequadamente os dados, os pontos traçados cairão aproximadamente ao longo de uma linha reta. Se os pontos traçados se desviarem significativamente de uma linha reta, o modelo hipotético não é apropriado.

Passo 3

Da maneira descrita anteriormente, nós construímos um gráfico de probabilidade normal. com base em observações 0.8406, 0.8104, 0.8234, 0.8108, 0.8235, 0.8562, 0.8123, 0.7076, 0.8184, 0.8265, 0.7773, 0.7871 é

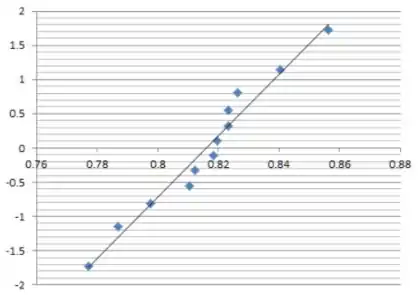
Um gráfico de probabilidade normal com base nas observações 0.8305, 0.7905, 0.8352, 0.8380, 0.8145, 0.8465, 0.8244, 0.8014, 0.8309, 0.8405, 0.8256, 0.8476 é

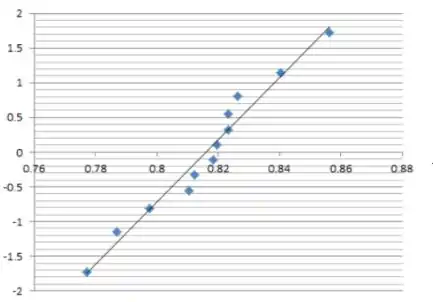
Os gráficos de probabilidade normal não contêm curvatura forte e o padrão é aproximadamente linear, então, eles indicam que não há problema com a suposição de normalidade ou com a suposição de variâncias iguais. Além disso, ambas as linhas retas têm inclinações semelhantes, fornecendo alguma verificação da suposição de alianças iguais.

Passo 4

Letra b:

Nós consideramos o teste de hipótese

H 0 : μ 1 = μ 2

contra

H 1 : μ 1 ≠ μ 2

Os dados são extraídos de distribuições normais e assumimos que σ 1 = σ 2 . Portanto, use o teste t agrupado.

A estatística é

t 0 = x - 1 - x - 2 - Δ 0 s p 1 n 1 + 1 n 2

Onde

s p = n 1 - 1 s 1 2 + n 2 - 1 s 2 2 n 1 + n 2 - 2 = 11 × 0.0217 2 + 11 × 0.0175 2 22 = 0.0197

Portanto,

t 0 = 0.8161 - 0.8271 - 0 0.0197 1 12 + 1 12 = - 1.37

Porque | t 0 | = 1.37 , encontramos na Tabela V do Apêndice que

P T n 1 + n 2 - 2 > t 0 = P T 22 > 1.37 < P T 22 > 1.321 = 0.1 P T n 1 + n 2 - 2 > t 0 = P T 22 > 1.37 > P T 22 > 1.717 = 0.05

Então, concluímos que os limites superior e inferior no valor P são:

0.1 < valor P  = 2 P T 22 > 1.37 < 0.2

Portanto, como o valor P é v a l o r   P > α = 0.05 , falhamos em rejeitar H 0 .

Passo 5

Letra c:

Um intervalo de confiança de 100 ( 1 - α ) % na diferença das médias μ 1 - μ 2 é

x - 1 - x - 2 - t α / 2 , n 1 + n 2 - 1 s p 1 n 1 + 1 n 2 ≤ μ 1 - μ 2 ≤ x - 1 - x - 2 + t α / 2 , n 1 + n 2 - 1 s p 1 n 1 + 1 n 2

Sabemos que α = 0.05 . Portanto, do Apêndice Tabela V obtemos

t 0,025,22 = 2.074

Portanto, um IC de 95% na diferença de médias μ 1 - μ 2 é

0.8161 - 0.8271 - 2.074 × 0.0197 2 12 ≤ μ 1 - μ 2 ≤ 0.8161 - 0.8271 + 2.074 × 0.0197 2 12

- 0.0277 ≤ μ 1 - μ 2 ≤ 0.0056

Observe que o intervalo de confiança de 95% inclui zero. Portanto, neste nível de confiança não podemos concluir que existe uma diferença nas médias.

Passo 6

Letra d:

Para o teste bilateral, quando σ 1 = σ 2 = σ e n 1 = n 2 = n , usamos os gráficos VIIe e VIIf com

d = Δ - Δ 0 2 σ ,

onde Δ é a verdadeira diferença nos meios que interessam. Para usar essas curvas, devemos ser inseridos com o tamanho da amostra n * = 2 n - 1 .

Sabemos que Δ = 0.2 e Δ 0 = 0 . Usando s P = 0.0197 como uma estimativa aproximada do desvio padrão comum σ , temos

d = 0.2 2 × 0.0197 = 5.077

E

n * = 2 × 12 - 1 = 23

Do Gráfico VIIe com d = 5.077 e n * = 23 , encontramos β ≈ 0 . Assim, o poder do teste na parte a) é

1 - β = 1

Passo 7

Letra e:

Agora, usamos β = 1 - 0.8 = 0.2 e a verdadeira diferença nas médias Δ = 0.1 . Portanto,

d = 0.1 2 × 0.0197 = 2.54

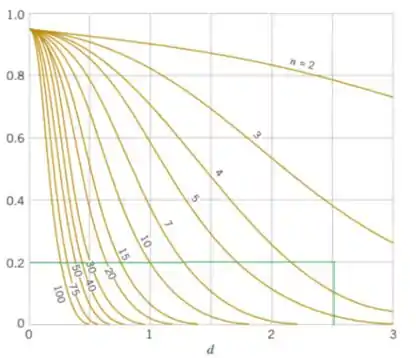
Do Gráfico VIIe, com d = 2.54 e β = 0.2 , encontramos n * ≈ 4 (veja a próxima figura, linha verde).

Portanto, como n * = 2 n - 1 :

n = n * + 1 2 = 2.5 ≈ 3

e usaríamos tamanhos de amostra de n 1 = n 2 = n = 3 .

Resposta

  1. Não há nenhum problema com a suposição de normalidade ou com a suposição de variâncias iguais.
  2. A estatística é t 0 =   - 1.77 . Falhamos em rejeitar H 0 , porque 0.1 < v a l o r   P < 0.2 .
  3. Um IC de 95 % é - 0.0277 ≤ μ 1 - μ 2 ≤ 0.0056 . Não podemos concluir que existe uma diferença de meios, porque o intervalo de confiança inclui zero.
  4. A potência do teste é 1 - β = 1
  5. Os tamanhos da amostra são n 1 = n 2 = n = 3
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sejam A a porcentagem de um elemento de um espécime de rocha selecionado aleatoriamente, e B a porcentagem de um segundo elemento desse mesmo espécime. Suponha que D e E sejam erros de medição ao dete
Um espécime de rocha de uma área específica é selecionado aleatoriamente e pesado duas vezes. Represente por W o peso real e por X 1 e X 2 os dois pesos medidos. Então, X 1 = W + E 1 e X 2 = W + E 2 ,
Sejam X 1 , … , X n vas independentes com valores médios μ 1 , … , μ n e variâncias σ 1 2 , … , σ n 2 . Considere uma função h x 1 , … , x n e use-a para definir uma nova va Y = h X 1 , … , X n . Sob
Uma aproximação mais precisa de E h X 1 , … , X n do Exercício 93 é h μ 1 , … , μ n + 1 2 σ 1 2 ∂ 2 h ∂ x 1 2 + ⋯ + 1 2 σ n 2 ∂ 2 h ∂ x n 2 Calcule-a para Y = h X 1 , X 2 , X 3 , X 4 , dado no Exercíc
a. X 1 tem distribuição qui-quadrado com parâmetro v 1 (veja a Seção 4.4), X 2 é independente de X 1 e tem uma distribuição qui-quadrado com parâmetro v 2 . Use a técnica do Exemplo 5.21 para mostrar