Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 10.Exercícios - Ex. 36

10-36. Dois diferentes testes analíticos podem ser usados para determi-

nar o nível de impurezas em ligas de aço. Oito cspécimes são lestados

usando amhos os procedimentos, sendo os resultados mostrados na ta-

bela a seguir.

a) Há evidéncia suficiente para concluir que os testes diferem no nível

medio de impureza? Use a = 0.01.

b) Há evidéncia para confirmar a atirmacao de que o Teste I gera uina

diferença media 0. I unidade menor do que o Teste 2? Lise a - 0.05.

c) Se a media do Teste I for O.l menor do que a média do Teste 2.é

importante detectar isse com uma probabil:dade de no minimo 0.90.

O uso ke 8ligas foi adcquado? Se não, quantas ligas deveriam ter

sido usadas?

Passo 1

Oi oi gente,

Vamos lá fazer mais uma questão passo a passo?

Vem comigo!

Dados:

n = 8 α = 0.01

Determine a diferença no valor de cada par:

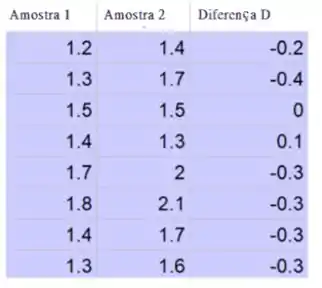
Passo 2

Letra a:

Determine as hipóteses:

H 0 : μ d = 0 H 1 : μ d ≠ 0

Determine a média da amostra das diferenças:

d - = - 0.2 - 0.4 + 0 + 0.1 - 0.3 - 0.3 - 0.3 - 0.3 8 ≈ - 0.2125

Determine o desvio padrão da amostra das diferenças:

s d = ( - 0.2 - ( - 0.2125 ) ) 2 + … + ( - 0.3 - ( - 0.2125 ) ) 2 8 - 1 ≈ 0.1727

Determine o valor de teste estatístico:

t = d - s d / n = - 0.2125 0.1727 / 8 ≈ - 3.480

O valor P é a probabilidade de obtenção do valor da estatística de teste ou um valor mais extremo. O valor P é o número (ou intervalo) no título da coluna da Tabela V contendo o valor t na linha d f = n - 1 = 8 - 1 = 7 :

0.01 = 2 × 0.005 < P < 2 × 0.01 = 0.02

Se o valor P for menor que o nível de significância, rejeita a hipótese nula.

P > 0.01 ⇒  Falha em rejetiar  H 0

Não há evidência suficiente para apoiar a alegação de que os testes diferem no nível médio de impureza.

Passo 3

Letra b:

α = 0.05

Determine as hipóteses:

H 0 : μ d = - 0.1 H 1 : μ d < - 0.1

Determine o valor de teste estatístico:

t = d - - μ d s d / n = - 0.2125 - ( - 0.1 ) 0.1727 / 8 ≈ - 1.842

O valor P é a probabilidade de obtenção do valor da estatística de teste ou um valor mais extremo. O valor P é o número (ou intervalo) no título da coluna da Tabela V contendo o valor t na linha d f = n - 1 = 8 - 1 = 7 :

0.05 < P < 0.10

Se o valor P for menor que o nível de significância, rejeita a hipótese nula.

P > 0.05 ⇒  Falha em rejeitar  H 0

Não há evidências suficientes para apoiar a afirmação de que o teste 1 gera uma diferença média de 0.1 unidades menor do que o teste 2.

Passo 4

Letra c:

Dados:

Δ = - 0.1 P o t ê n c i a = 0.90 α = 0.05

β   é o complemento da potência, assim, 1 diminuída pela potência:

β = 1 - P o t ê n c i a = 1 - 0.90 = 0.10

Fórmula do tamanho da amostra:

n = z α + z β 2 σ 2 Δ - Δ 0 2

Δ é a hipótese nula em μ 1 - μ 2 = Δ 0

Δ é a hipótese alternativa μ 1 - μ 2 = Δ

Determine z α = z 0.05 usando a tabela de probabilidade normal no apêndice (procure 0.05 na tabela, o valor z é então o valor z encontrado com sinal oposto):

z α = 1.64

Determine z β = z 0.10 usando a tabela de probabilidade normal no apêndice (procure 0.10 na tabela, o valor z é então o valor z encontrado com sinal oposto):

z β = 1.28

Preencha os valores dados na fórmula e avalie (arredondado para cima):

n 1 = n 2 = ( 1.64 + 1.28 ) 2 0.1727 2 ( - 0.1 - 0 ) 2 = 25

O tamanho da amostra de 8 não é adequado, porque o tamanho mínimo da amostra necessário para detectar uma diferença de 0.1 é 25.

Resposta

  1. Não há evidências suficientes para apoiar a alegação de que os testes diferem no nível médio de impureza.
  2. Não há evidências suficientes para apoiar a alegação de que o teste 1 gera uma diferença média de 0.1 unidades menor do que o teste 2.
  3. Não é adequado, n = 25
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sejam XeY variáveis aleatórias independentes com distribuição uniforme em θ - 1 2 ; θ + 1 2 , onde θ ∈ R . Mostre que a distribuição de Z = X - Y não depende de θ .
Se XeY são variáveis aleatórias independentes com funções densidade iguais a f x = e - xp a r ax0 , obtenha a densidade conjunta de X + Ye3 X + 2 Y . Neste caso, X + Ye3 X + 2 Y são independentes?
Suponha que X 1 ,X 2 ,X 3 representam as componentes da velocidade de uma molécula de gás. Suponha que X 1 ,X 2 ,eX 3 são independentes, cada uma com densidade normal média 0 a variância σ 2 , σ0 . Di
Suponha que as dimensões A e B de uma chapa retangular de aço produzida por uma indústria sejam variáveis aleatórias independentes com as seguintes funções densidades de probabilidade, f A x = x - 1 ,
Quando uma corrente elétrica I (medida em ampères) passa através de uma resistência R (medida em ohms), a potência gerada é dada por W = R I 2 (medida em watts). Suponha que IeR são variáveis aleatóri