10-37. Lim artigo na revista Neurologyt1998.Vol.50.pp.12-46-1252)

gemeos monozigotos dividem inúmeras earacteristicas fí-

sieas. psieológicas e patológicas. Os investigadores mediram um grau

de inieligência de 1O pares de gémeos, sendo os dados apresentados a

seguir:

a) A suposição de que a diferença no grau seja normalmente distribu-

ída é razoável? Mosire resultados para confirmar a sua resposta.

b) Encontre um intervalo de confiaga de 95se para a diferenca no grau

medio. Há alguina evidéncia de que o grau médio depende da or-

dem de naseimento?

c) E importante detectar uma diferença média de um ponto no grau.

com uma probabilidade de no minimo 0.90. O uso de 10 pares foi

adequado? Se não. quantos pares devenam ter sido usados?

Letra a:

Determine a média da amostra das diferenças:

Determine o desvio padrão da amostra das diferenças:

Gráfico da probabilidade normal:

Os valores dos dados estão no eixo horizontal e as pontuações normais padronizadas estão no eixo vertical.

Se os dados contiverem n valores de dados, então as pontuações normais padronizadas são os valores z na tabela III correspondendo a uma área de (ou a área mais próxima) com .

A menor pontuação padronizada corresponde à menor quantidade de dados, a segunda menor pontuação padronizada corresponde ao segundo menor valor de dados e assim por diante.

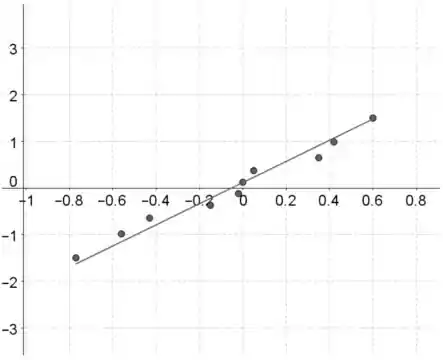
A suposição normal parece ser razoável, porque o padrão no gráfico de probabilidade normal é aproximadamente linear e não contém nenhuma curvatura forte.

Letra b:

Determine usando a tabela V com :

Os pontos finais do intervalo de confiança são:

Não há evidências suficientes para apoiar a reivindicação depende da ordem de nascimento, porque o intervalo de confiança contém 0 e, portanto, as médias não parecem diferir.

Letra c:

Dados:

é o complemento da potência, assim, 1 diminuída pela potência:

Fórmula do tamanho da amostra:

é a hipótese nula em

é a hipótese alternativa

Determine usando a tabela de probabilidade normal no apêndice (procure 0.05 na tabela, o valor z é então o valor z encontrado com sinal oposto):

Determine usando a tabela de probabilidade normal no apêndice (procure 0.10 na tabela, o valor z é então o valor z encontrado com sinal oposto):

Preencha os valores dados na fórmula e avalie (arredondado para cima):

O tamanho da amostra de 10 é adequado, porque o tamanho mínimo da amostra necessário para detectar uma diferença de 1 é 3 (menos de 10).