Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 11.Exercícios - Ex. 15
11-15.Em um artigo cm Statisties and Computing, "An iterative Monte
Carlo method for nonconjugate bavesian unulysis" - Um método
interativo de Monte ('arlo para uma análisc baycsiana não conjugada".(1991. pp. 119-128). Carlin e Geltand investigaram a idade(x)e o com-
primento (y) de 27 vacas do mar (dugongs) capturadas.
a) Encontre as estimativas de mínimos quadrados da inclinação e da
interseção para o modelo de regressão linear simples. Qual é a esti-
mativa de o ?
b) Estime o comprimento médio das vacas do mar quando elas tiverem
Il anos.
c) Ohtenha os valores ajustados , que correspondem a cada valor ob.
servado de y. Faca um grálico de y, versus v. e comente o que esse
gráfico pareceria se a relação linear entre o comprimento c a idade
fosse perfeitamente determinística (nenhum erro). Esse gráfico in
dica quc a idade é uma escolha razoável de variável regressora nes-
se modelo?
Passo 1
Oi oi gente,
Vamos lá fazer mais uma questão passo a passo?
Vem comigo!
Dados:
Letra a:
As estimativas de mínimos quadrados da interceptação e inclinação são:
A linha de regressão de mínimos quadrados torna-se então:
Determine a soma dos erros quadrados:
é então estimado pela soma dos erros quadráticos divididos pelo tamanho da amostra diminuída por 2:
Passo 2
Letra b:
Substitua x na linha de regressão de mínimos quadrados por 11 e avalie:
Passo 3
Letra c:
Os valores y estão no eixo horizontal e os valores ajustados estão no eixo vertical.
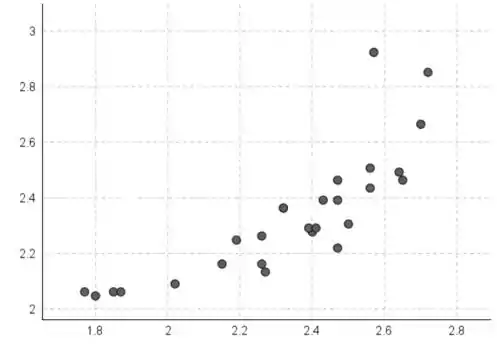
Resposta
- Não