Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 11.Exercícios - Ex. 70
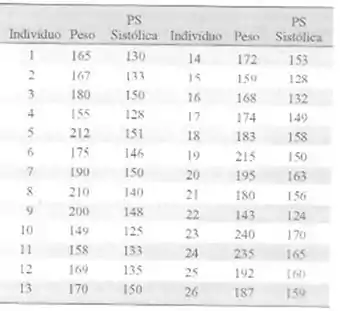
11.70. Os dados referentes ao peso e a pressão sangüínea sistólica de
26 homens selecionados aleatoriamente. na faixa etárna de 25 a 30 anos.
são mostrados na tahela seguinte. Considere que o peso e a pressão san-
guinea estejam distribuidos normal e conjuntamente.
a) Encontre a linha de regressão relacionando a pressão sanguinea sis-
tólica ao peso.
b) Teste a significância da regressão usando a - 0,05.
c) Estime o coeficiente de correlacão.
d)Teste a hipotese de quc p = O usando a = 0.05.
e) Teste a hipútese de que p-0.6 usando a 0,05.
f) Construa um intervalo de confiança de 9554 para o coeficiente de
correlação.
Passo 1
Faaaaaaala aí gente,
Vamos fazer uma daquelas questões passo a passo?
Vem comigo!!
Dados:
Letra a:
Encontre como foi feito na tabela abaixo.
Agora, encontre a soma de cada coluna para obter:
E então, use a fórmula a seguir para obter o coeficiente de correlação
Substitua a e b na fórmula da equação de regressão:
Passo 2
Letra b:
Encontre como foi feito na tabela abaixo.
Agora, encontre a soma de cada coluna para obter:
E então, use a fórmula a seguir para obter o coeficiente de correlação
Passo 3
O valor da estatística de teste é:
Determine a probabilidade correspondente (valor P) usando a tabela V com
Se o valor P for menor que o nível de significância, vamos rejeitar a hipótese nula:
Existem evidências suficientes para apoiar a alegação de que existe uma correlação linear e existem evidências suficientes para apoiar a alegação de que a regressão é significativa.
Passo 4
Letra c:
Encontre como foi feito na tabela abaixo.
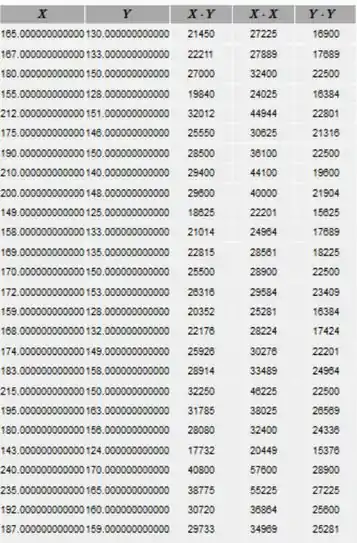
Agora, encontre a soma de cada coluna para obter:
E então, use a fórmula a seguir para obter o coeficiente de correlação
Passo 5
Letra d:
O valor da estatística de teste é:
Determine a probabilidade correspondente (valor P) usando a tabela V com
Se o valor P for menor que o nível de significância, vamos rejeitar a hipótese nula:
Existem evidências suficientes para apoiar a alegação de que existe uma correlação linear.
Passo 6
Letra e:
O valor da estatística de teste é:
Determine a probabilidade correspondente (valor P) usando a tabela V com
Se o valor P for menor que o nível de significância, vamos rejeitar a hipótese nula:
Existem evidências suficientes para apoiar a afirmação de que existe uma correlação linear.
Passo 7
Letra f:
Para o nível de confiança , determine usando a tabela III (procure 0.025 na tabela, o valor z é então o valor z encontrado com sinal oposto):
Os limites do intervalo de confiança para o coeficiente de correlação são então:
Resposta
- Existem evidências suficientes para apoiar a alegação de que existe uma correlação linear e existem evidências suficientes para apoiar a alegação de que a regressão é significativa
- Existem evidências suficientes para apoiar a alegação de que existe uma correlação linear
- Existem evidências suficientes para apoiar a alegação de que existe uma correlação linear