Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 11.Exercícios - Ex. 72
11-72. A cstimativa absoluta mensal ds indiees globais (terra c mar
combinados) da temperatura i'C) em 2000 e 2001 são (fonte: http://
www.ncdc.noaa.gov/oa/climate/research/monitoring.html)
a) Faça um gráfico c ajuste uma linha de regressão para prever as tem-
peraturas de 2001 a partir daquelas de 2000. Ilá uma regressão sig-
nificativa para a = 0,05? Qual é o valor P?
b) Estime o coefieiente de correlaçào.
c)Tesle a hipútese de que p - 0,9 contra a alternativa p -0.9 usando
a-0.05.Qual é o valor P?
d) Caleule um intervalo de confiança de 95% para o coeficiente de
correlação.
Passo 1
Faaaaaaala aí gente,
Vamos fazer uma daquelas questões passo a passo?
Vem comigo!!
Dados:
Letra a:
2000 está no eixo horizontal e 2001 está no eixo vertical.
Passo 2
Determine a equação de regressão de mínimos quadrados:
Primeiro, vamos encontrar , como foi feito na tabela abaixo:
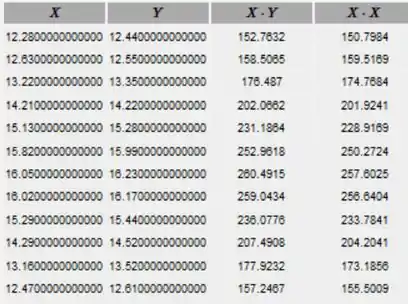
Encontre a soma de cada coluna:
Use as seguintes equações para encontrar a e b:
Substitua a e b na equação da fórmula de regressão
Passo 3
Determine o coeficiente de correlação linear r:
Encontre como foi feito na tabela abaixo.
Agora, encontre a soma de cada coluna para obter:
E então, use a fórmula a seguir para obter o coeficiente de correlação
Passo 4
O valor da estatística de teste é:
Determine a probabilidade correspondente (valor P) usando a tabela V com
Se o valor P for menor que o nível de significância, vamos rejeitar a hipótese nula:
Existem evidências suficientes para apoiar a alegação de que existe uma correlação linear e existem evidências suficientes para apoiar a alegação de que a regressão é significativa.
Passo 5
Letra b:
Encontre como foi feito na tabela abaixo.
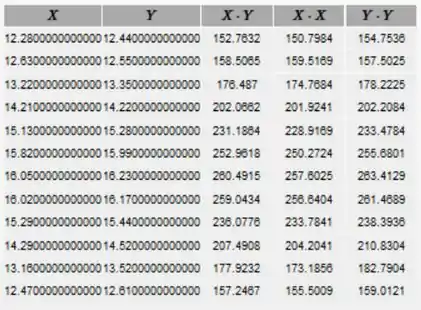
Agora, encontre a soma de cada coluna para obter:
E então, use a fórmula a seguir para obter o coeficiente de correlação
Passo 6
Letra c:
O valor da estatística de teste é:
Determine a probabilidade correspondente (valor P) usando a tabela V com
Se o valor P for menor que o nível de significância, vamos rejeitar a hipótese nula:
Existem evidências suficientes para apoiar a alegação de que existe uma correlação linear.
Passo 7
Letra d:
Para o nível de confiança , determine usando a tabela III (procure 0.025 na tabela, o valor z é então o valor z encontrado com sinal oposto):
Os limites do intervalo de confiança para o coeficiente de correlação são então:
Resposta
- . Existem evidências suficientes para apoiar a alegação de que existe uma correlação linear e existem evidências suficientes para apoiar a alegação de que a regressão é significativa.
- Existem evidências suficientes para apoiar a alegação de que existe uma correlação linear.