11-77. Uma utilidade elétrica está interessada em desenvolver um mo-
delo relacionando demanda na hora de pko y. em quilowatis) e o con-
sumo inensal total de energia (x. em quilowatt horas). Dados para 50
consumidores residenciais são mostrados na tabela seguinte.
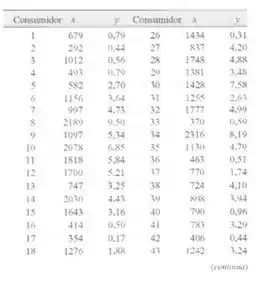
a) Desenhe um diagrama de dispersão desses dados.
b) Ajusle um modclo de regressao linear.
c) Teste a significância da regressão usando a= 0.05.
d) Faça um grafico dos reviduos do modelo de regressão versus
xe
comente as suposicões bavicas de egressao. Especificamente.pare
ce que a suposicao de igualdade de variância é satisfeita?
e) Encontre um modclo de regressão linear simples usando vy como a
resposta. EEssa Iransformação em vestabiliza o probiema de desigual-
dade de variáncia motado no item d) anterior?.
Passo 1
Faaaaaaala aí gente,
Vamos fazer uma daquelas questões passo a passo?
Vem comigo!!
Letra a:
Denotemos as variáveis no exercício como x e y. Então, depois de processar os dados fornecidos na tabela, chegamos ao seguinte gráfico de dispersão dos dados:
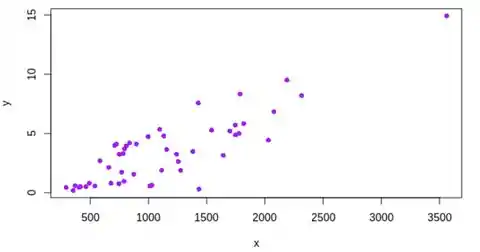
Passo 2
Letra b:
Agora ajustamos o modelo linear aos dados. Primeiro, vamos calcular as quantidades importantes (nota ).
Agora estamos prontos para determinar os coeficientes do modelo:
Portanto, o melhor ajuste linear para os dados é:
Passo 3
Letra c:
Precisamos testar a significância da regressão. Neste exercício, vamos optar pela abordagem de análise de variância para este problema.
Primeiro, avaliamos a regressão e a soma dos quadrados dos erros:
para calcular o valor da estatística F:
Rejeitamos então primeiro determine:
e, então, obviamente rejeitamos por causa da enorme estatística de teste que obtivemos.
Passo 4
Letra d:
Plotamos os resíduos versus os valores ajustados e descobrimos que o gráfico sugere que o modelo não é totalmente adequado! A variância não parece homogênea.
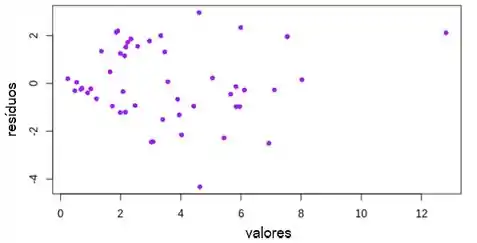
Passo 5
Letra e:
Repetimos o procedimento, agora com os valores de em vez de y.
O modelo linear assim obtido é
Vemos no gráfico abaixo que a nova variância parece mais "igual".
:
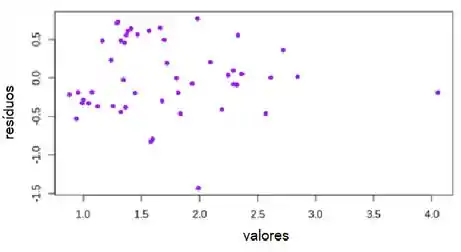
Resposta
- Ver resolução
- Rejeitamos a hipótese nula (valor p quase 0), concluindo que a regressão é significativo.
- A igualdade da variância não é satisfeita.
Melhor igualdade de variância.