Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 61
Os autores do artigo “Objective Effects of a Six Months' Endurance and Strength Training Program in Outpatients with Congestive Heart Failure” (Medicine and Science in Sports and Exercise, 1999, p. 1102–1107) apresentaram uma análise de correlação para investigar a relação entre o nível máximo de lactato x e a resistência muscular y. Os dados a seguir foram reproduzidos de um gráfico desse artigo.
O gráfico de dispersão mostra um padrão linear. a. Verifique se existe uma correlação positiva entre o nível máximo de lactato e a resistência muscular na população da qual esses dados foram selecionados. b. Se uma análise de regressão tivesse de ser realizada para prever a resistência muscular com base no nível de lactato, que proporção de variação observada na resistência podia ser atribuída à relação linear aproximada? Responda a essa mesma pergunta se a regressão for usada para prever o nível de lactato com base na resistência – e responda a ambas as perguntas sem fazer nenhum cálculo de regressão
Passo 1
- O coeficiente de correlação da amostra r é dado por
- A relação entre o coeficiente de correlação da amostra e o coeficiente de determinação é dada por
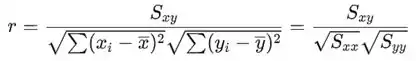
Onde
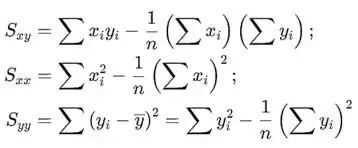
que são dados no exercício. O coeficiente de correlação da amostra r pode ser calculado usando valores fornecidos como
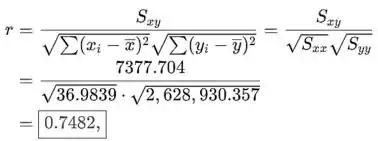
o que indica que não existe uma relação linear forte (também não é pequena).
Ao testar versus uma das alternativas, a estatística de teste é
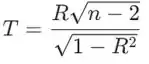
que tem distribuição t com n-2 graus de liberdade, onde R é o coeficiente de correlação amostral como variável aleatória. Dependendo da hipótese alternativa, o valor de P é a área correspondente sob curva.
A hipótese alternativa é . O valor da estatística T é
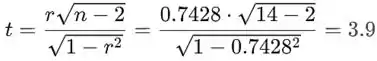
Passo 2
O valor de P é
que foi calculado por meio de um software. Porque
rejeitar a hipótese nula em qualquer nível de significância razoável α e concluir que variáveis são positivamente relacionadas linearmente - a correlação é positiva
Passo 3
assim, o coeficiente de determinação, ou a proporção de variação observada é
O coeficiente de determinação não mudará se você alterar o preditor (porque r não mudaria). Por causa da definição de r
não importa como você rotula as variáveis - o coeficiente de correlação da amostra permaneceria o mesmo.
Resposta
- A correlação é positiva