Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 7.Exercícios - Ex. 65
7-65.Quando uma populacio tem uma distribuicao normal,o estimador
ealgumas vezes usado para estimar o desvio-padrao da populacao.
Esse estimador e mais robusto em relacao a outliers do que o desvio-padrao usual da amostra e geralmente nao difere muito de S quando nao ha observacoes nao-usuais.
（a)Calcule re S para os dados:10,12,9,14,18,15c16.
（b)Troque a primeira observacao na amostra(10)por 50 e recalcule
Passo 1
Quando a população tem uma distribuição normal, o estimador às vezes é usado para estimar o desvio padrão da população.
Letra a:
Vamos calcular e para os dados 10,12.9,14,18,15 e 16.
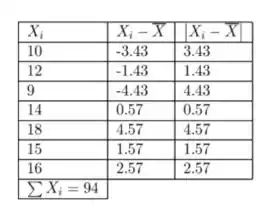
Passo 2
Para encontrar a mediana dos dados acima, primeiro, temos que organizar os dados da última coluna em ordem crescente
0.57, 1.43, 1.57, 2.57, 3.43, 4.43, 4.57
Como o número total de observações é ímpar, a mediana é o meio da observação, 2.57.
Conseqüentemente
Agora vamos calcular o desvio padrão da amostra
Passo 3
Letra b:
Vamos calcular e para os dados 50, 12, 9, 14, 18, 15 e 16.
Para encontrar a mediana dos dados acima, primeiro, temos que organizar os dados
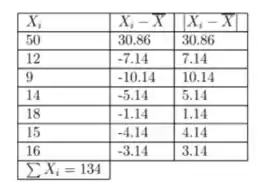
da última coluna em ordem crescente.
1.14, 3.14, 4.14, 5.14, 7.14, 10.14, 30.86
Passo 4
Como o número total de observações é ímpar, a mediana é o meio da observação, 5.14.
Então,
Agora vamos calcular o desvio padrão da amostra