Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 9.Exercícios - Ex. 49
. Acredita-se que a capa frontal e a natureza da primeira pergunta de pesquisas por correspondência influenciem o índice de respostas. O artigo "The Impact of Cover Design and First Questions on Response Rates for a Mail Survey of Skydivers" (Leisure Sciences, 1991, p. 67-76) testou essa teoria, fazendo experimentos com diferentes modelos de capas. Uma capa era lisa, a outra tinha a figura de um pára-quedista. Os pesquisadores consideraram que o índice de retorno seria menor para a capa lisa
Esses dados confirmam a hipótese dos pesquisadores? Teste as hipóteses relevantes, usando 0,10, calculando primeiro um valor P
Passo 1
Deixe seja a proporção da população daqueles que responderam a uma cobertura simples, e seja seja a proporção populacional daqueles que responderam a uma capa com uma foto de paraquedista. Deixe que e ser as estimativas da amostra de e , respectivamente (ou seja, as proporções da amostra daqueles que responderam a cobertura simples e a cobertura com uma foto de paraquedista, respectivamente).
Como a capa simples foi enviada para m = 207 participantes, e nessa amostra, X = 104 devolveu a capa, então a estimativa amostral é
Da mesma forma, a capa com a foto do paraquedista foi enviada para n=213 indivíduos, e nessa amostra, Y=109 devolveu a capa, então a estimativa amostral é
Nós queremos testar:
no nível de significância
Desde
então as suposições necessárias para usar a estatística do teste Z são válidas.
Passo 2
A estatística de teste usada para testar essas hipóteses é
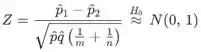
que, sob a hipótese nula, segue aproximadamente uma distribuição normal padrão.
Aqui, é a proporção da amostra combinada, calculada como
E simplesmente é
Substituindo todos os valores,
Passo 3
O teste é de cauda inferior, então o valor P deste teste é a área sob a curva de densidade da distribuição normal padrão, à esquerda do valor da estatística de teste , ou seja,
O valor pode ser encontrado na Tabela A.3 nas Tabelas do Apêndice.
Encontramos a linha rotulada com "-0.1" e a coluna rotulada com ".09" (isso corresponde ao valor -0.19), e então o valor desejado é encontrado no corpo da tabela, sob essa linha e coluna, e podemos descobrir que é
Como o valor P deste teste é maior que nosso nível de significância , então falhamos em rejeitar a hipótese nula, ou seja, não temos evidências suficientes para confirmar a especulação dos pesquisadores de que a taxa de retorno é menor para a cobertura plana do que para a cobertura com uma foto de paraquedista nela
Resposta
O valor da estatística de teste é com o valor P de , então não rejeitamos a hipótese nula.