Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 9.Exercícios Suplementares - Ex. 75
As informações sobre a postura e a força da mão geradas pelos dedos durante a manipulação diária de vários objetos são necessárias para projetar dispositivos protéticos de alta tecnologia para mão. O artigo "Grip Posture and Forces During Holding Cylindrical Objects with Circular Grips" (Ergonomics, 1996, p. 1163-1176) relatou que, para uma amostra de 11 mulheres, a força média amostral à contração de quatro dedos (N) foi 98,1, e o desvio padrão amostral, 14,2. Para uma amostra de 15 homens, a média e o desvio padrão amostrais foram 129,2 e 39,1, respectivamente. a. Um teste realizado para ver se as resistências médias reais dos dois sexos eram diferentes resultou em t 2,51 e valor P 0,019. O procedimento de teste apropriado descrito neste capítulo produz esse valor de t e o valor P determinado? b. Existe evidência substancial de que a resistência média real dos homens excede a das mulheres por mais de 25 N? Expresse e teste as hipóteses relevantes.
Passo 1
- Reivindicação dada: Difere
- Reivindicação dada: Mais de 25
A afirmação é a hipótese nula ou a hipótese alternativa. A hipótese nula e a hipótese alternativa afirmam o oposto uma da outra. A hipótese nula precisa conter uma igualdade.
Determine a estatística de teste:
Determine os graus de liberdade (arredondados para o inteiro mais próximo):
O valor P é a probabilidade de obter o valor da estatística de teste, ou um valor mais extremo. O valor P é o número (ou intervalo) no título da coluna da distribuição T de Student no apêndice contendo o valor t na linha df=18:
Notamos então que o valor t dado não está correto.
Passo 2
A afirmação é a hipótese nula ou a hipótese alternativa. A hipótese nula e a hipótese alternativa afirmam o oposto uma da outra. A hipótese nula precisa conter uma igualdade.
Determine a estatística de teste:
Determine os graus de liberdade (arredondados para o inteiro mais próximo):
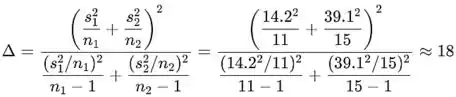
O valor P é a probabilidade de obter o valor da estatística de teste, ou um valor mais extremo. O valor P é o número (ou intervalo) no título da coluna da distribuição T de Student no apêndice contendo o valor t na linha df=18:
Se o valor P for menor ou igual ao nível de significância, então a hipótese nula é rejeitada:
Não há evidências suficientes para apoiar a afirmação de que a força média real para homens excede a das mulheres em mais de 25 N.
Resposta
- Não há evidências suficientes para apoiar a afirmação de que a força média real para os homens excede a das mulheres em mais de 25 N.