Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 3.Exercícios - Ex. 16

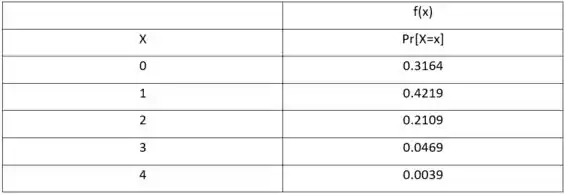
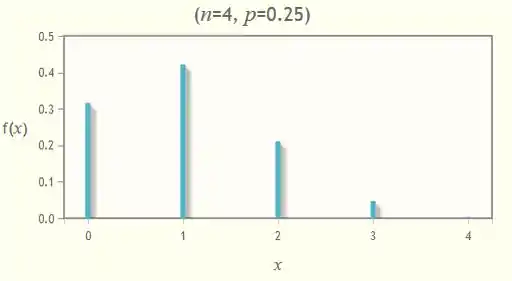
Algumas partes da Califórnia são particularmente propensas a terremotos. Suponha que em tal área, 30% de todos os moradores tenham seguro contra danos por terremotos. Quatro moradores são selecionados aleatoriamente. Seja X o número dos que possuem seguro contra danos por terremotos, entre os quatro. a. Determine a distribuição de probabilidades de X. [Sugestão: seja S o morador que tem seguro e N o que não o tem. Uma possibilidade será SNSS, com probabilidade (0,3)(0,7)(0,3)(0,3) e valor associado X 3. Há outros 15 resultados]. b. Desenhe o histograma de probabilidade correspondente. c. Qual é o valor mais provável de X? d. Qual é a probabilidade de que ao menos dois dos quatro moradores selecionados tenham seguro?

Passo 1

Dado:

n = 4

p = 25 % = 0.25

Definição de probabilidade binomial:

Passo 2

  1. Seja SS um proprietário que tem seguro e FF um proprietário que não tem seguro. Os eventos possíveis são então:

    2. {SSSS,SSSF,SSFS,SSFF,SFSS,SFSF,SFFS,SFFF,FSSS, FSSF, FSFS, FSFF, FFSS, FFSF, FFFS, FFFF, FSSS,FSSF,FSFS,FSFF,FFSS,FFSF,FFFS,FFFF}

    O evento SSSSSSSS corresponde a X=4.

    Os eventos SSSF, SSFS, SFSS, FSSSSSSF,SSFS,SFSS,FSSS correspondem a X=3.

    Os eventos SSFF, SFSF, SFFS, FSSF, FSFS, FFSSSSFF,SFSF,SFFS,FSSF,FSFS,FFSS correspondem a X=3.

    Os eventos FFFS, FFSF, FSFF, SFFFFFFS,FFSF,FSFF,SFFF correspondem a X=1.

    O evento FFFFFFFF corresponde a X=0.

    Preencha os valores conhecidos na definição de probabilidade binomial:

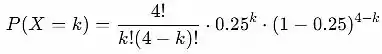
  2. A largura das barras deve ser a mesma e a altura deve ser igual à probabilidade.

  3. O valor mais provável é X=1, porque a probabilidade de X=1 é a mais alta e a barra mais alta na parte (b) corresponde a X=1.

    4. Passo 3

  4. Regra de adição para eventos disjuntos ou mutuamente exclusivos:

P A   o u   B = P A + P B

Adicione as probabilidades dos eventos correspondentes:

P X   ≥ 2 = P   X = 2 + P X = 3 + P X = 4 = 0.2109 + 0.0469 + 0.0039 = 0.2617

Resposta

Ver o desenvolvimento

Exercícios de Livros Relacionados

Supondo que a proporção de crianças do sexo masculino numa comunidade de famílias se de 2/5, qual a probabilidade de, numa família de 5 crianças, encontrarmos:Todas crianças do mesmo sexo;Exatamente 4
Uma empresa compra matrizes para gráfica em pacotes contendo 5 matrizes. Sabe-se que 20% das matrizes compradas têm defeitos de fabricação que implicam na sua inutilização. Calcular a probabilidade de
O setor de controle de qualidade de uma fábrica testa 6 peças de cada lote de 80 unidades recebidas, adotando o seguinte critério: se for encontrada no máximo 1 peça defeituosa, o lote é aceito normal
Uma empresa decidiu fabricar paralamas de automóveis a partir de chapas importadas por via marítima, as quais vem acondicionadas em embalagens de 6 chapas cada. Tendo a empresa verificado que 5% das c
Um avião tem 4 turbinas (2 em cada lado); sabe-se que a probabilidade de cada turbina falhar numa viagem transoceânica é de 8% (falhas independentes entre si). Calcular, numa viagem dessas, a probabil